苏科版九年级数学下册第7章锐角三角函数 单元同步训练(含答案)
文档属性
| 名称 | 苏科版九年级数学下册第7章锐角三角函数 单元同步训练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 418.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 10:51:44 | ||
图片预览


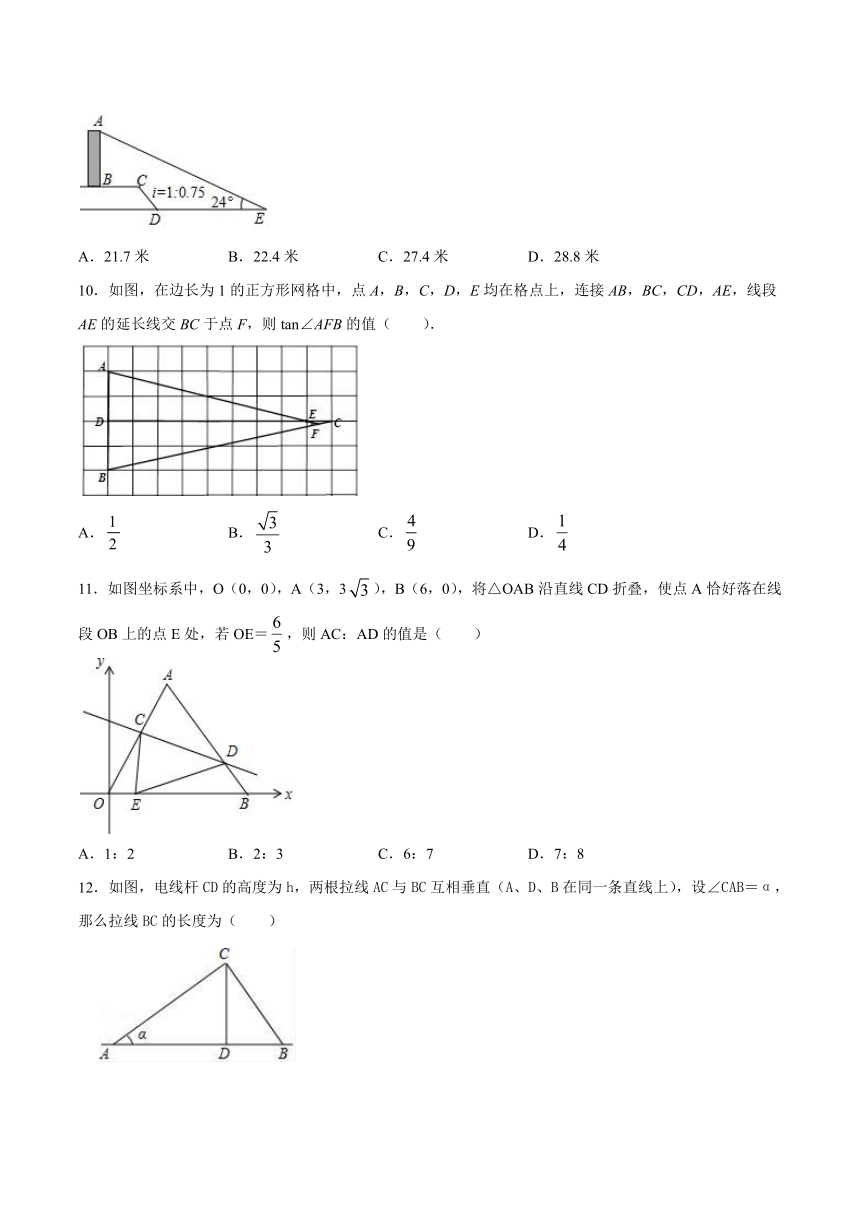
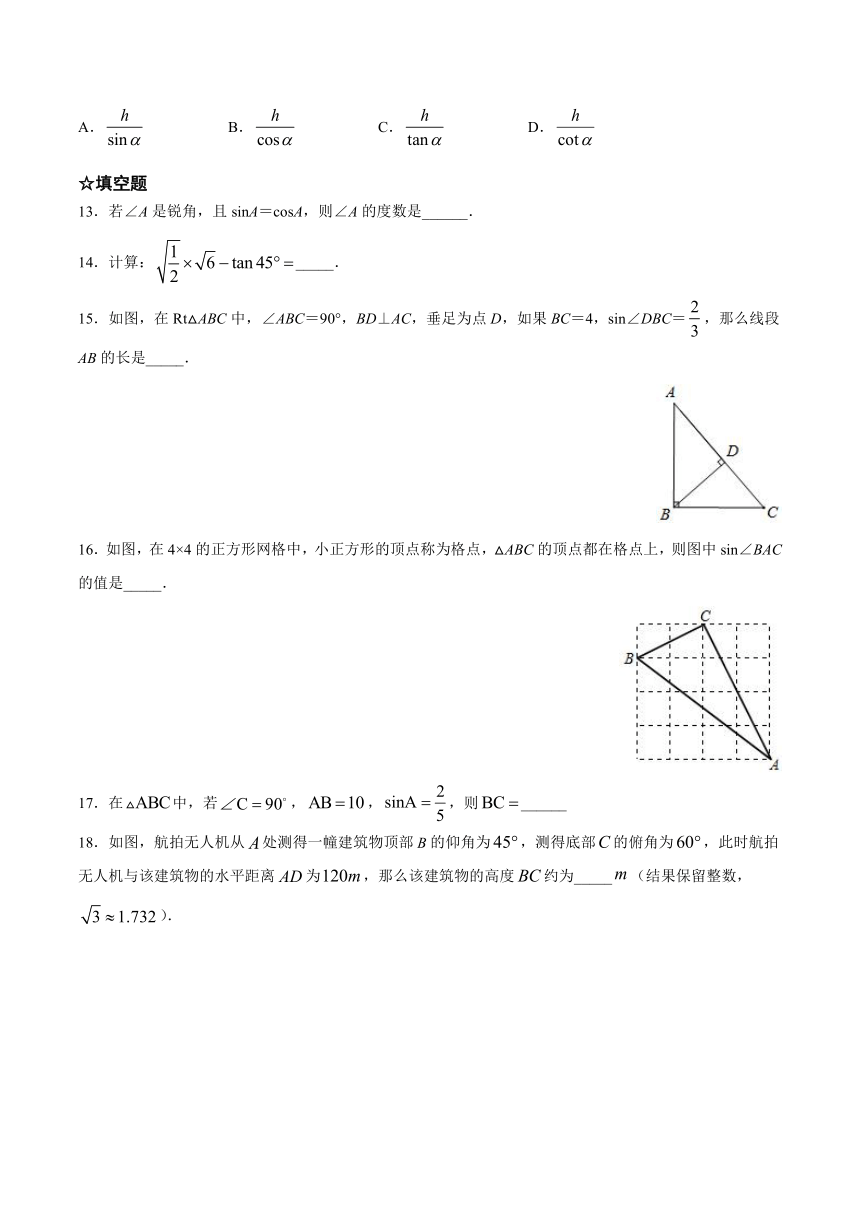
文档简介
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
(苏科版)九年级数学第二学期锐角三角函数同步达标训练
☆选择题(请在下面的四个选项中将正确的答案选在括号里)
1.如果∠a是等边三角形的一个内角,那么cosa的值等于(
).
A.
B.
C.
D.
2.如图,在中,,,,将绕点逆时针旋转得到,使得点落在上,则的值为(
)
A.
B.
C.
D.
3.的值等于(
)
A.
B.
C.
D.
4.如图,△ABC的顶点都在正方形网格的格点上,则cos∠BAC的值为(
)
A.
B.
C.
D.
5.如图,在菱形ABCD中,DE⊥AB,cosA=,则cos∠DBE的值是( )
A.
B.
C.
D.
6.如图,一块矩形木板ABCD斜靠在墙边,(,点A、B、C、D、O在同一平面内),已知,,.则点A到OC的距离等于(
)
A.
B.
C.
D.
7.在中,,若,则等于(
)
A.
B.1
C.
D.
8.小华和妈妈到大足北山游玩,身高1.5米的小华站在坡度为的山坡上的点观看风景,恰好看到对面的多宝塔,测得眼睛看到塔顶的仰角为,接着小华又向下走了米,刚好到达坡底,这时看到塔顶的仰角为,则多宝塔的高度约为(
).(精确到0.1米,参考数据:)
A.51.0米
B.52.5米
C.27.3米
D.28.8米
9.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米
B.22.4米
C.27.4米
D.28.8米
10.如图,在边长为1的正方形网格中,点A,B,C,D,E均在格点上,连接AB,BC,CD,AE,线段AE的延长线交BC于点F,则tan∠AFB的值(
).
A.
B.
C.
D.
11.如图坐标系中,O(0,0),A(3,3),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=,则AC:AD的值是(
)
A.1:2
B.2:3
C.6:7
D.7:8
12.如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A.
B.
C.
D.
☆填空题
13.若∠A是锐角,且sinA=cosA,则∠A的度数是______.
14.计算:_____.
15.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为点D,如果BC=4,sin∠DBC=,那么线段AB的长是_____.
16.如图,在4×4的正方形网格中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中sin∠BAC的值是_____.
17.在中,若,,,则______
18.如图,航拍无人机从处测得一幢建筑物顶部的仰角为,测得底部的俯角为,此时航拍无人机与该建筑物的水平距离为,那么该建筑物的高度约为_____(结果保留整数,).
19.若,那么△ABC的形状是___.
20.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的F处,如果,那么tan∠DCF的值是____.
☆解答题
21.(1)计算(﹣2)3++|1﹣|0﹣4sin60°
(2)化简代数式,再从﹣2≤a≤2中选一个恰当的整数作为a的值,代入求值.
22.如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.求:(1)点B的坐标;(2)cos∠BAO的值.
23.夏季是垂钓的好季节.一天甲、乙两人到松花江的处钓鱼,突然发现在处有一人不慎落入江中呼喊救命.如图,在处测得处在的北偏东方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从处跳水游向处救人;此时乙从沿岸边往正东方向奔跑40米到达处,再从处下水游向处救人,已知处在的北偏东方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
(1)求、的长.
(2)试问甲、乙二人谁能先救到人,请通过计算说明理由.()
24.如图1,△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,过点C作CF//BD,交AB于点E,交AD于点F.
(1)求证:△AEF≌△BEC;
(2)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,如图2,求sin∠ACH的值.
25.某公园有一座古塔,古塔前有一个斜坡坡角,斜坡高米,平行于水平地面的一个平台.小华想利用所学知识测量古塔的高度她在平台的点处水平放置--平面镜,并沿着方向移动,当移动到点时,刚好在镜面中看到古塔顶端点的像,这时,测得小华眼睛与地面的距离米,米,米,米,已知请你根据题中提供的相关信息,求出古塔的高度.(参考数据:)
26.在Rt△ACB中,∠ACB=90°,点D为AB上一点.
(1)如图1,若CD⊥AB,求证:CD2=AD?DB;
(2)如图2,若AC=BC,EF⊥CD于H,EF与BC交于E,与AC交于F,且=,求的值;
(3)如图3,若AC=BC,点H在CD上,且∠AHD=45°,CH=3DH,直接写出tan∠ACH的值为
.
27.已知抛物线的顶点,经过点,与轴分别交于,两点.
(1)求该抛物线的解析式;
(2)如图1,点是抛物线上的一个动点,且在直线的下方,过点作轴的平行线与直线交于点,当取最大值时,求点的坐标;
(3)如图2,轴交轴于点,点是抛物线上,之间的一个动点,直线,与分别交于,,当点运动时.
①直接写出的值;
②直接写出的值.
参考答案
1.A2.B3.A4.C5.C6.C7.C8.B9.A10.A11.B12.B
13.45°
14.
15.2.
16..
17.4
18.328
19.等边三角形
20..
21.(1)2﹣2;(2),当a=0时,原式=2;当a=﹣1时,原式=.
22.(1);(2).
23.(1)米,米,(2)乙先到达救人地点.
24.(1)略;(2)
25.古塔的高度为米.
26.(1)略;(2);(3)
27.(1);(2)(3)①8;②4
答案第2页,总2页
(苏科版)九年级数学第二学期锐角三角函数同步达标训练
☆选择题(请在下面的四个选项中将正确的答案选在括号里)
1.如果∠a是等边三角形的一个内角,那么cosa的值等于(
).
A.
B.
C.
D.
2.如图,在中,,,,将绕点逆时针旋转得到,使得点落在上,则的值为(
)
A.
B.
C.
D.
3.的值等于(
)
A.
B.
C.
D.
4.如图,△ABC的顶点都在正方形网格的格点上,则cos∠BAC的值为(
)
A.
B.
C.
D.
5.如图,在菱形ABCD中,DE⊥AB,cosA=,则cos∠DBE的值是( )
A.
B.
C.
D.
6.如图,一块矩形木板ABCD斜靠在墙边,(,点A、B、C、D、O在同一平面内),已知,,.则点A到OC的距离等于(
)
A.
B.
C.
D.
7.在中,,若,则等于(
)
A.
B.1
C.
D.
8.小华和妈妈到大足北山游玩,身高1.5米的小华站在坡度为的山坡上的点观看风景,恰好看到对面的多宝塔,测得眼睛看到塔顶的仰角为,接着小华又向下走了米,刚好到达坡底,这时看到塔顶的仰角为,则多宝塔的高度约为(
).(精确到0.1米,参考数据:)
A.51.0米
B.52.5米
C.27.3米
D.28.8米
9.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米
B.22.4米
C.27.4米
D.28.8米
10.如图,在边长为1的正方形网格中,点A,B,C,D,E均在格点上,连接AB,BC,CD,AE,线段AE的延长线交BC于点F,则tan∠AFB的值(
).
A.
B.
C.
D.
11.如图坐标系中,O(0,0),A(3,3),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=,则AC:AD的值是(
)
A.1:2
B.2:3
C.6:7
D.7:8
12.如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A.
B.
C.
D.
☆填空题
13.若∠A是锐角,且sinA=cosA,则∠A的度数是______.
14.计算:_____.
15.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为点D,如果BC=4,sin∠DBC=,那么线段AB的长是_____.
16.如图,在4×4的正方形网格中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中sin∠BAC的值是_____.
17.在中,若,,,则______
18.如图,航拍无人机从处测得一幢建筑物顶部的仰角为,测得底部的俯角为,此时航拍无人机与该建筑物的水平距离为,那么该建筑物的高度约为_____(结果保留整数,).
19.若,那么△ABC的形状是___.
20.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的F处,如果,那么tan∠DCF的值是____.
☆解答题
21.(1)计算(﹣2)3++|1﹣|0﹣4sin60°
(2)化简代数式,再从﹣2≤a≤2中选一个恰当的整数作为a的值,代入求值.
22.如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.求:(1)点B的坐标;(2)cos∠BAO的值.
23.夏季是垂钓的好季节.一天甲、乙两人到松花江的处钓鱼,突然发现在处有一人不慎落入江中呼喊救命.如图,在处测得处在的北偏东方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从处跳水游向处救人;此时乙从沿岸边往正东方向奔跑40米到达处,再从处下水游向处救人,已知处在的北偏东方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
(1)求、的长.
(2)试问甲、乙二人谁能先救到人,请通过计算说明理由.()
24.如图1,△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,过点C作CF//BD,交AB于点E,交AD于点F.
(1)求证:△AEF≌△BEC;
(2)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,如图2,求sin∠ACH的值.
25.某公园有一座古塔,古塔前有一个斜坡坡角,斜坡高米,平行于水平地面的一个平台.小华想利用所学知识测量古塔的高度她在平台的点处水平放置--平面镜,并沿着方向移动,当移动到点时,刚好在镜面中看到古塔顶端点的像,这时,测得小华眼睛与地面的距离米,米,米,米,已知请你根据题中提供的相关信息,求出古塔的高度.(参考数据:)
26.在Rt△ACB中,∠ACB=90°,点D为AB上一点.
(1)如图1,若CD⊥AB,求证:CD2=AD?DB;
(2)如图2,若AC=BC,EF⊥CD于H,EF与BC交于E,与AC交于F,且=,求的值;
(3)如图3,若AC=BC,点H在CD上,且∠AHD=45°,CH=3DH,直接写出tan∠ACH的值为
.
27.已知抛物线的顶点,经过点,与轴分别交于,两点.
(1)求该抛物线的解析式;
(2)如图1,点是抛物线上的一个动点,且在直线的下方,过点作轴的平行线与直线交于点,当取最大值时,求点的坐标;
(3)如图2,轴交轴于点,点是抛物线上,之间的一个动点,直线,与分别交于,,当点运动时.
①直接写出的值;
②直接写出的值.
参考答案
1.A2.B3.A4.C5.C6.C7.C8.B9.A10.A11.B12.B
13.45°
14.
15.2.
16..
17.4
18.328
19.等边三角形
20..
21.(1)2﹣2;(2),当a=0时,原式=2;当a=﹣1时,原式=.
22.(1);(2).
23.(1)米,米,(2)乙先到达救人地点.
24.(1)略;(2)
25.古塔的高度为米.
26.(1)略;(2);(3)
27.(1);(2)(3)①8;②4
答案第2页,总2页
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
