湘教版九年级数学下册2.7正多边形与圆同步测试含答案
文档属性
| 名称 | 湘教版九年级数学下册2.7正多边形与圆同步测试含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 284.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 00:00:00 | ||
图片预览



文档简介
2.7
正多边形与圆
同步测试
选择题
1.下列说法正确的是(
)
A.各边都相等的多边形是正多边形
B.一个圆有且只有一个内接正多边形
C.圆内接正四边形的边长等于半径
D.圆内接正n边形的中心角度数为
2.如图,正五边形ABCDE内接于⊙O,则∠ADE的度数是
(
)
A.60°
B.45°
C.
36°
D.
30°
3.若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于(
)
A.
B.
C.
D.
4.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是
A.?115°????B.?l05°????C.?100°????D.?95°
5.(2019·自贡)图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近(
)
A.
B.
C.
D.
6.如图,⊙O过正方形ABCD的顶点A,B,且与CD相切,若正方形ABCD的边长为2,则⊙O的半径为( )
A.1
B.
C.
D.
7.如图,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件错误的是( )
A.∠ACD=∠DAB
B.AD=DE
C.AD2=BD·CD
D.CD·AB=AC·BD
8.如图,要拧开一个边长为a=6
mm的正六边形螺帽,扳手张开的开口b至少为(
)
A.6
mm
B.12
mm
C.6
mm
D.4
mm
如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是(
).
A.60°
B.45°
C.30°
D.22.5°
如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则的值为(
)
A.
B.
C.
D.
二、填空题
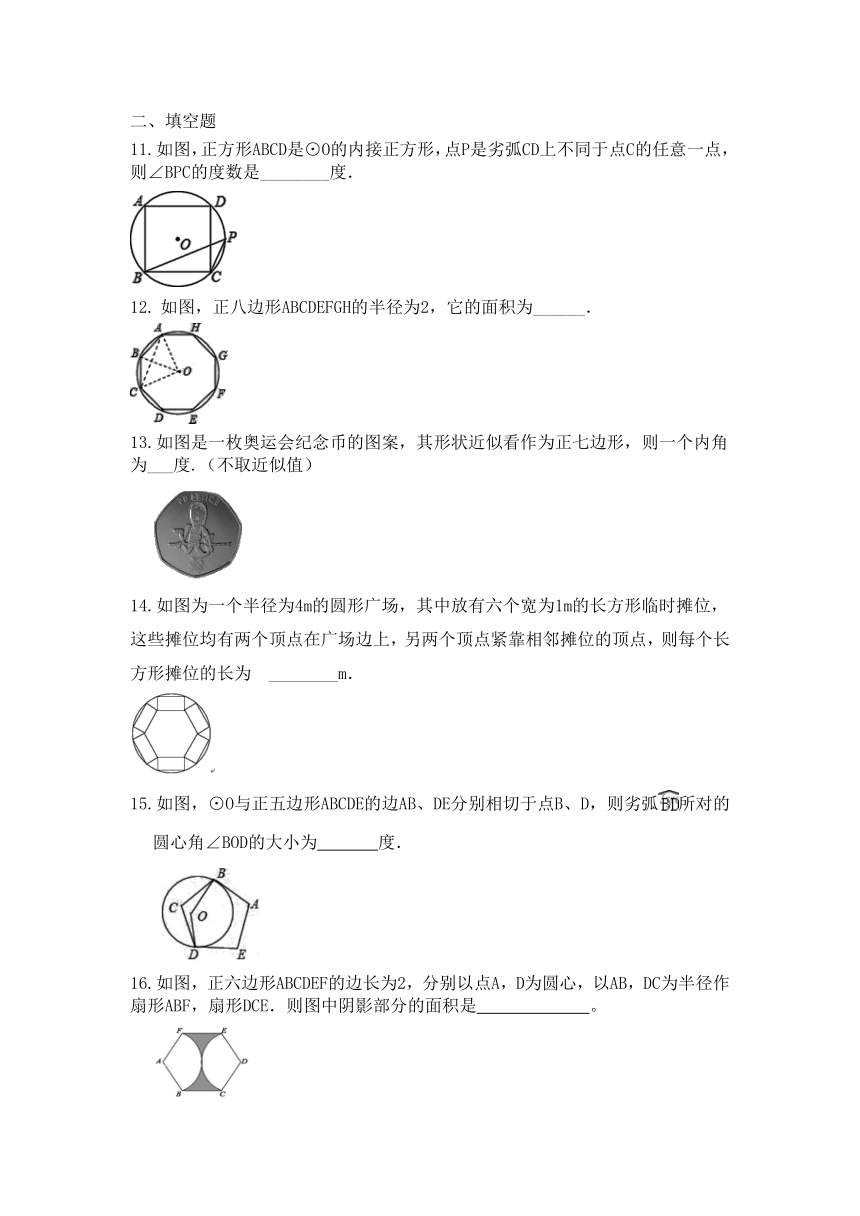
11.如图,正方形ABCD是⊙O的内接正方形,点P是劣弧CD上不同于点C的任意一点,则∠BPC的度数是________度.
如图,正八边形ABCDEFGH的半径为2,它的面积为______.
13.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为___度.(不取近似值)
14.如图为一个半径为4m的圆形广场,其中放有六个宽为1m的长方形临时摊位,这些摊位均有两个顶点在广场边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为?________m.
15.如图,⊙O与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角∠BOD的大小为
度.
16.如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF,扇形DCE.则图中阴影部分的面积是
。
三、综合题
17.如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD?DC=PA?BC.
18.如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
19.(2019浙江省杭州市)如图,已知锐角三角形ABC内接于⊙O,OD⊥BC于点D.连接0A.
(1)若∠BAC=60°,
①求证:OD=OA.
②当OA=1时,求△ABC面积的最大值.
(2)点E在线段0A上.OE=OD.连接DE,设∠ABC=m∠OED.∠ACB=n∠OED(m,n是正数).
若∠ABC<∠ACB.求证:m-n+2=0
20.如图,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连结AE交⊙O于点F,连结BF并延长交CD于点G.
(1)求证:△ABE≌△BCG;
(2)若∠AEB=55°,OA=3,求劣弧BF的长.(结果保留π)
2.7
正多边形与圆同步测试答案
选择题
1.D
2.C
3.A
4.B
5.C
6.D
7.D
8.C
9.C
10.B
二、填空题
11.45
12.
13.
14.
15.144
16.
三、综合题
17.证明:如图,连接AC,连接BD.
∵DP∥AC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB.
∴△PAD∽△DCB.
得PA:DC=AD:BC,
即AD?DC=PA?BC.
18.(1)∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
AB=BC
角ABM=角C
BM=CN
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC=(5-2)×180÷5=108°.
即∠APN的度数为108°.
19.解:(1)①连接OB、OC,
则∠BOD=BOC=∠BAC=60°,
∴∠OBC=30°,
∴OD=OB=OA;
②∵BC长度为定值,
∴△ABC面积的最大值,要求BC边上的高最大,
当AD过点O时,AD最大,即:AD=AO+OD=,
△ABC面积的最大值=×BC×AD=×2OBsin60°×=;
(2)如图2,连接OC,
设∠OED=x,则∠ABC=mx,∠ACB=nx,
则∠BAC=180°-∠ABC-∠ACB=180°-mx-nx=∠BOC=∠DOC,
∵∠AOC=2∠ABC=2mx,∴∠AOD=∠COD+∠AOC=180°-mx-nx+2mx=180°+mx-nx,
∵OE=OD,∴∠AOD=180°-2x,即:180°+mx-nx=180°-2x,化简得:m-n+2=0.
20.解:(1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,
∴∠ABE=∠BCG=∠AFB=90°,
∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,
∴∠EBF=∠BAF,
在△ABE与△BCG中,,
∴△ABE≌△BCG(ASA);
(2)解:连接OF,
∵∠ABE=∠AFB=90°,∠AEB=55°,
∴∠BAE=90°﹣55°=35°,
∴∠BOF=2∠BAE=70°,
∵OA=3,
∴弧BF的长=.
正多边形与圆
同步测试
选择题
1.下列说法正确的是(
)
A.各边都相等的多边形是正多边形
B.一个圆有且只有一个内接正多边形
C.圆内接正四边形的边长等于半径
D.圆内接正n边形的中心角度数为
2.如图,正五边形ABCDE内接于⊙O,则∠ADE的度数是
(
)
A.60°
B.45°
C.
36°
D.
30°
3.若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于(
)
A.
B.
C.
D.
4.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是
A.?115°????B.?l05°????C.?100°????D.?95°
5.(2019·自贡)图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近(
)
A.
B.
C.
D.
6.如图,⊙O过正方形ABCD的顶点A,B,且与CD相切,若正方形ABCD的边长为2,则⊙O的半径为( )
A.1
B.
C.
D.
7.如图,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件错误的是( )
A.∠ACD=∠DAB
B.AD=DE
C.AD2=BD·CD
D.CD·AB=AC·BD
8.如图,要拧开一个边长为a=6
mm的正六边形螺帽,扳手张开的开口b至少为(
)
A.6
mm
B.12
mm
C.6
mm
D.4
mm
如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是(
).
A.60°
B.45°
C.30°
D.22.5°
如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则的值为(
)
A.
B.
C.
D.
二、填空题
11.如图,正方形ABCD是⊙O的内接正方形,点P是劣弧CD上不同于点C的任意一点,则∠BPC的度数是________度.
如图,正八边形ABCDEFGH的半径为2,它的面积为______.
13.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为___度.(不取近似值)
14.如图为一个半径为4m的圆形广场,其中放有六个宽为1m的长方形临时摊位,这些摊位均有两个顶点在广场边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为?________m.
15.如图,⊙O与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角∠BOD的大小为
度.
16.如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF,扇形DCE.则图中阴影部分的面积是
。
三、综合题
17.如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD?DC=PA?BC.
18.如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
19.(2019浙江省杭州市)如图,已知锐角三角形ABC内接于⊙O,OD⊥BC于点D.连接0A.
(1)若∠BAC=60°,
①求证:OD=OA.
②当OA=1时,求△ABC面积的最大值.
(2)点E在线段0A上.OE=OD.连接DE,设∠ABC=m∠OED.∠ACB=n∠OED(m,n是正数).
若∠ABC<∠ACB.求证:m-n+2=0
20.如图,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连结AE交⊙O于点F,连结BF并延长交CD于点G.
(1)求证:△ABE≌△BCG;
(2)若∠AEB=55°,OA=3,求劣弧BF的长.(结果保留π)
2.7
正多边形与圆同步测试答案
选择题
1.D
2.C
3.A
4.B
5.C
6.D
7.D
8.C
9.C
10.B
二、填空题
11.45
12.
13.
14.
15.144
16.
三、综合题
17.证明:如图,连接AC,连接BD.
∵DP∥AC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB.
∴△PAD∽△DCB.
得PA:DC=AD:BC,
即AD?DC=PA?BC.
18.(1)∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
AB=BC
角ABM=角C
BM=CN
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC=(5-2)×180÷5=108°.
即∠APN的度数为108°.
19.解:(1)①连接OB、OC,
则∠BOD=BOC=∠BAC=60°,
∴∠OBC=30°,
∴OD=OB=OA;
②∵BC长度为定值,
∴△ABC面积的最大值,要求BC边上的高最大,
当AD过点O时,AD最大,即:AD=AO+OD=,
△ABC面积的最大值=×BC×AD=×2OBsin60°×=;
(2)如图2,连接OC,
设∠OED=x,则∠ABC=mx,∠ACB=nx,
则∠BAC=180°-∠ABC-∠ACB=180°-mx-nx=∠BOC=∠DOC,
∵∠AOC=2∠ABC=2mx,∴∠AOD=∠COD+∠AOC=180°-mx-nx+2mx=180°+mx-nx,
∵OE=OD,∴∠AOD=180°-2x,即:180°+mx-nx=180°-2x,化简得:m-n+2=0.
20.解:(1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,
∴∠ABE=∠BCG=∠AFB=90°,
∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,
∴∠EBF=∠BAF,
在△ABE与△BCG中,,
∴△ABE≌△BCG(ASA);
(2)解:连接OF,
∵∠ABE=∠AFB=90°,∠AEB=55°,
∴∠BAE=90°﹣55°=35°,
∴∠BOF=2∠BAE=70°,
∵OA=3,
∴弧BF的长=.
