数学四年级下青岛版五四制2整理复习《多边形的面积》课件(17张ppt)
文档属性
| 名称 | 数学四年级下青岛版五四制2整理复习《多边形的面积》课件(17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 22:45:17 | ||
图片预览



文档简介
(共17张PPT)
好习惯:
1.课前准备:笔、本、作业、学具……。
2.良好的听课环境。
优品质:
1.认真听。
2.仔细做。
3.勤思考。
4.善总结。
5.活运用。
多边形的面积单元复习
青岛版四年级下册第二单元
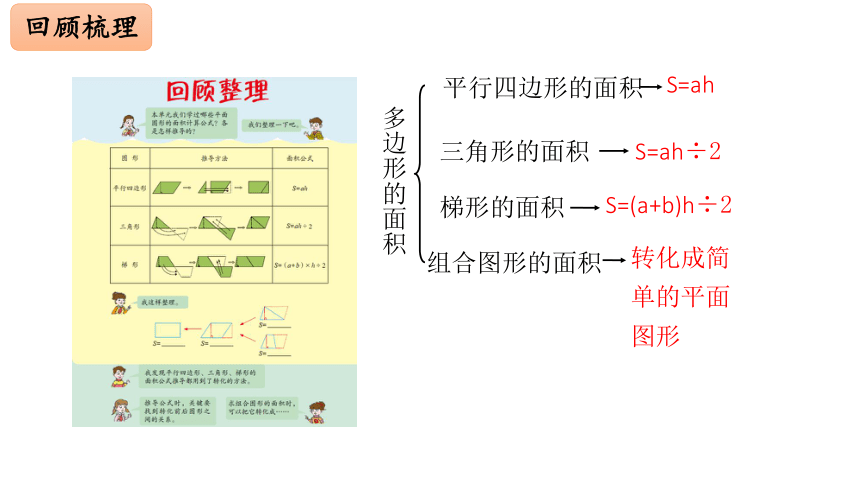
平行四边形的面积
三角形的面积
组合图形的面积
S=ah
S=ah÷2
梯形的面积
S=(a+b)h÷2
转化成简单的平面图形
多边形的面积
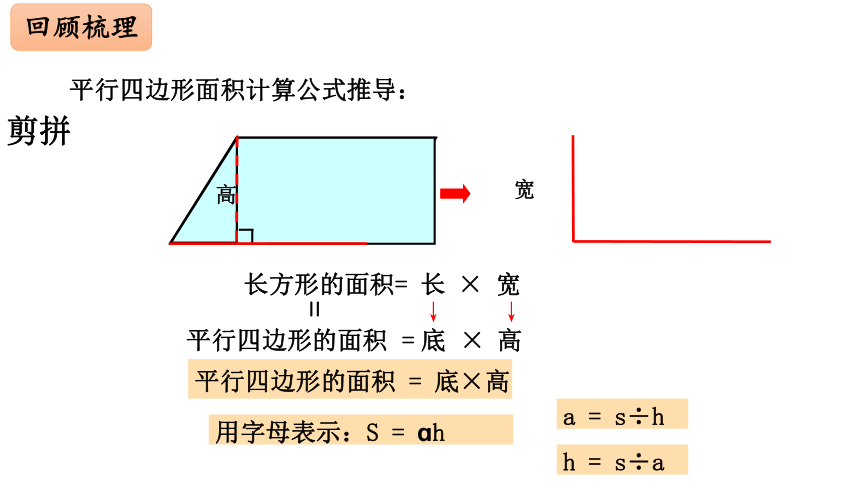
回顾梳理
平行四边形的面积
=
底×高
高
宽
用字母表示:S
=
ɑh
长方形的面积=
长
×
宽
平行四边形的面积
=
↓
↓
底
高
×
=
平行四边形面积计算公式推导:
a
=
s÷h
h
=
s÷a
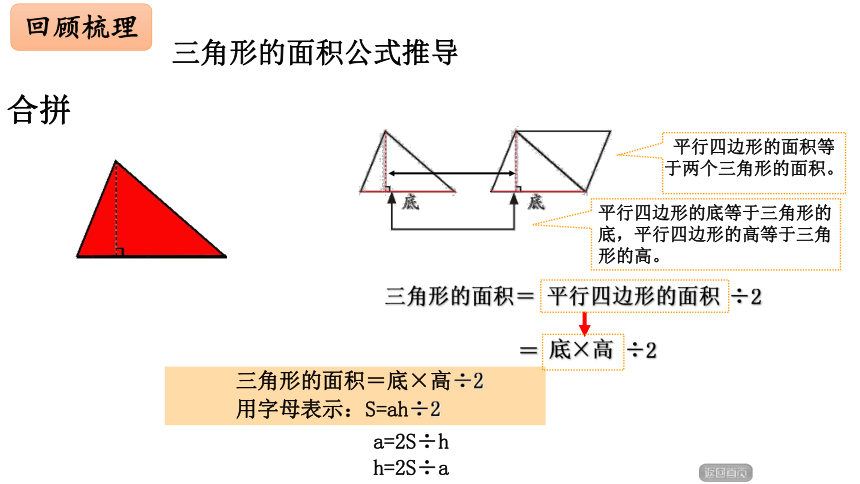
回顾梳理
剪拼
三角形的面积公式推导
回顾梳理
三角形的面积=
三角形的面积=底×高÷2
用字母表示:S=ah÷2
÷2
平行四边形的面积等于两个三角形的面积。
平行四边形的面积
÷2
底×高
=
平行四边形的底等于三角形的底,平行四边形的高等于三角形的高。
a=2S÷h
h=2S÷a
合拼
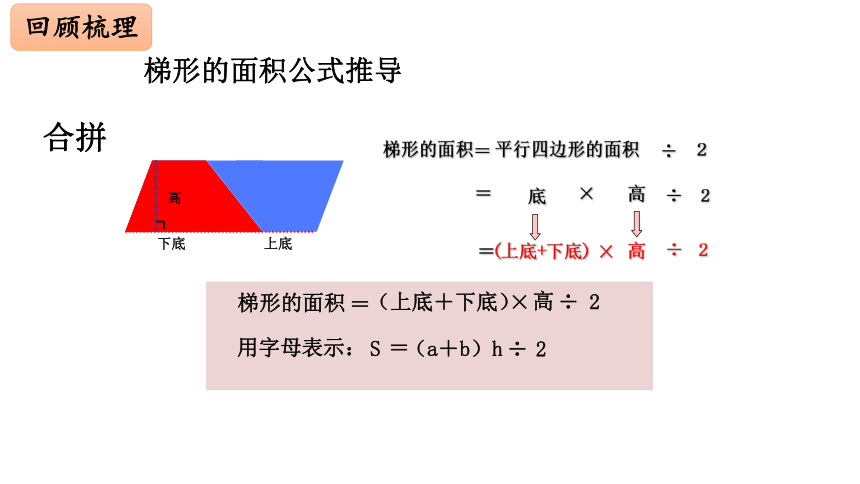
梯形的面积
÷
2
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
=
梯形的面积
=
×
高
÷
2
用字母表示:
S
(上底+下底)
=
(a+b)
h
÷
2
高
下底
上底
回顾梳理
梯形的面积公式推导
合拼
4cm
10cm
12cm
8cm
组合图形的面积
分割法:将组合图形分割成两个或两个以上的基本图形的方法。
S组合图形=S三角形+S长方形
(10-4)×(12-8)÷2=12(cm2)
8×10=80(cm2
)
12+80=92(cm2
)
4cm
10cm
12cm
8cm
添补法:通过添加辅助线,几个组合图形转化成基本图形的方法。
S组合图形
=
S大长方形-S梯形
12×10=120(cm2
)
(4+10)×(12-8)÷2=28(cm2
)
120-28=92(cm2
)
组合图形转化成几个学过的基本图形
要根据图形的特点,确定是用“割”还是用“补”的方法,“割”或“补”后的图形都应是规范图形,而且“割”或“补”的平面图形越少越好,容易计算,?“割”我们用加法算,“补”我们用减法计算。
回顾梳理
a
a
a
b
a
b
h
h
a
h
S=ah
S=ah÷2
S=(a+b)h÷2
转化
转化
转化
a
b
S=ab
图形之间的关系:
推导
推导
推导
回顾梳理
推导面积公式时都用转化了的方法
多边形的面积
平行四边形的面积
三角形的面积
梯形的面积
组合图形的面积
知识结构图
S=ah
S=ah÷2
S=(a+b)h÷2
转化成求几个简单的平面图形面积的和或差
h=S÷a
a=S÷h
h=2S÷a
a=2S÷h
h=2S÷a(a+b)
a+b=2S÷h
转化
转化
回顾梳理
习题讲解
一、求出下面平行四边形的面积。
16m
9m
∟
∟
24dm
9dm
8dm
二、下面的平行四边形中,AC的长度是多少厘米?
∟
A
B
7cm
∟
3cm
6.25
C
D
习题讲解
三、求出下面三角形的底或高。
∟
96㎡
16m
?
∟
15cm
225c㎡
?
习题讲解
四、一种流动红旗的底是28厘米,高是35厘米。如果需要做12面这样的流动红旗,至少需要多少平方厘米的红丝绸?
习题讲解
五、求X的值。
3m
20㎡
∟
7m
Xm
6dm
10dm
Xdm
40d㎡
习题讲解
六、李爷爷在自家院内用篱笆靠墙围了一块梯形菜地(如下图),已知篱笆的长是35.2米,其中一条边的长是7.2米,这块菜地的面积是多少平方米?
习题讲解
七、求出下面多边形的面积。单位(cm)
1.8
0.3
2
0.5
2
12
15
5
5
5
习题讲解
八、在(
)内填上“>、<或=”。
5公顷(
)5000平方米
28平方千米(
)280000平方米
150公顷(
)1.5平方千米
438平方米(
)4.38公顷
习题讲解
好习惯:
1.课前准备:笔、本、作业、学具……。
2.良好的听课环境。
优品质:
1.认真听。
2.仔细做。
3.勤思考。
4.善总结。
5.活运用。
多边形的面积单元复习
青岛版四年级下册第二单元
平行四边形的面积
三角形的面积
组合图形的面积
S=ah
S=ah÷2
梯形的面积
S=(a+b)h÷2
转化成简单的平面图形
多边形的面积
回顾梳理
平行四边形的面积
=
底×高
高
宽
用字母表示:S
=
ɑh
长方形的面积=
长
×
宽
平行四边形的面积
=
↓
↓
底
高
×
=
平行四边形面积计算公式推导:
a
=
s÷h
h
=
s÷a
回顾梳理
剪拼
三角形的面积公式推导
回顾梳理
三角形的面积=
三角形的面积=底×高÷2
用字母表示:S=ah÷2
÷2
平行四边形的面积等于两个三角形的面积。
平行四边形的面积
÷2
底×高
=
平行四边形的底等于三角形的底,平行四边形的高等于三角形的高。
a=2S÷h
h=2S÷a
合拼
梯形的面积
÷
2
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
=
梯形的面积
=
×
高
÷
2
用字母表示:
S
(上底+下底)
=
(a+b)
h
÷
2
高
下底
上底
回顾梳理
梯形的面积公式推导
合拼
4cm
10cm
12cm
8cm
组合图形的面积
分割法:将组合图形分割成两个或两个以上的基本图形的方法。
S组合图形=S三角形+S长方形
(10-4)×(12-8)÷2=12(cm2)
8×10=80(cm2
)
12+80=92(cm2
)
4cm
10cm
12cm
8cm
添补法:通过添加辅助线,几个组合图形转化成基本图形的方法。
S组合图形
=
S大长方形-S梯形
12×10=120(cm2
)
(4+10)×(12-8)÷2=28(cm2
)
120-28=92(cm2
)
组合图形转化成几个学过的基本图形
要根据图形的特点,确定是用“割”还是用“补”的方法,“割”或“补”后的图形都应是规范图形,而且“割”或“补”的平面图形越少越好,容易计算,?“割”我们用加法算,“补”我们用减法计算。
回顾梳理
a
a
a
b
a
b
h
h
a
h
S=ah
S=ah÷2
S=(a+b)h÷2
转化
转化
转化
a
b
S=ab
图形之间的关系:
推导
推导
推导
回顾梳理
推导面积公式时都用转化了的方法
多边形的面积
平行四边形的面积
三角形的面积
梯形的面积
组合图形的面积
知识结构图
S=ah
S=ah÷2
S=(a+b)h÷2
转化成求几个简单的平面图形面积的和或差
h=S÷a
a=S÷h
h=2S÷a
a=2S÷h
h=2S÷a(a+b)
a+b=2S÷h
转化
转化
回顾梳理
习题讲解
一、求出下面平行四边形的面积。
16m
9m
∟
∟
24dm
9dm
8dm
二、下面的平行四边形中,AC的长度是多少厘米?
∟
A
B
7cm
∟
3cm
6.25
C
D
习题讲解
三、求出下面三角形的底或高。
∟
96㎡
16m
?
∟
15cm
225c㎡
?
习题讲解
四、一种流动红旗的底是28厘米,高是35厘米。如果需要做12面这样的流动红旗,至少需要多少平方厘米的红丝绸?
习题讲解
五、求X的值。
3m
20㎡
∟
7m
Xm
6dm
10dm
Xdm
40d㎡
习题讲解
六、李爷爷在自家院内用篱笆靠墙围了一块梯形菜地(如下图),已知篱笆的长是35.2米,其中一条边的长是7.2米,这块菜地的面积是多少平方米?
习题讲解
七、求出下面多边形的面积。单位(cm)
1.8
0.3
2
0.5
2
12
15
5
5
5
习题讲解
八、在(
)内填上“>、<或=”。
5公顷(
)5000平方米
28平方千米(
)280000平方米
150公顷(
)1.5平方千米
438平方米(
)4.38公顷
习题讲解
