数学五年级下青岛版五四制4《圆柱的表面积》整理复习课件(13张ppt)
文档属性
| 名称 | 数学五年级下青岛版五四制4《圆柱的表面积》整理复习课件(13张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 689.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 16:04:36 | ||
图片预览


文档简介
(共13张PPT)
《圆柱的表面积》整理复习
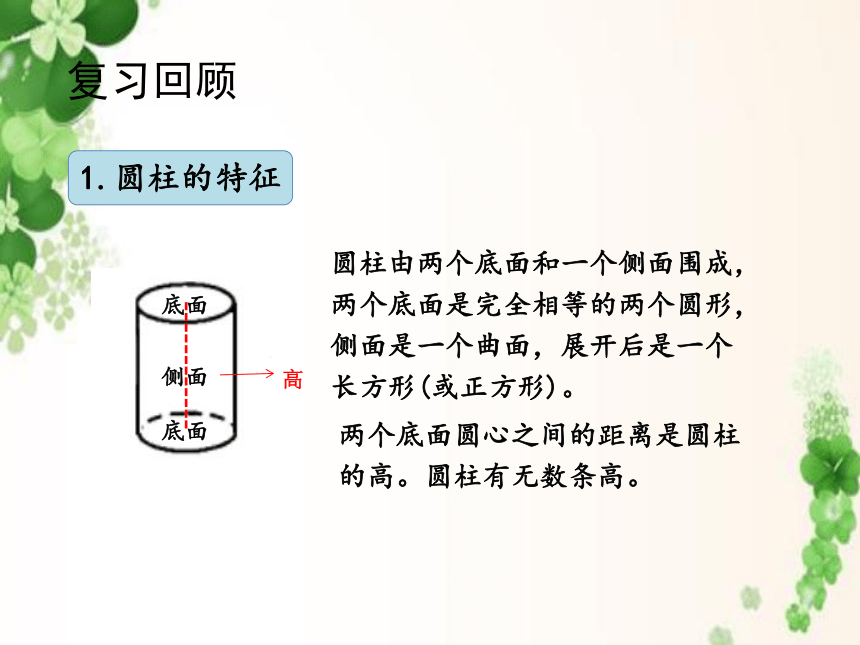
1.圆柱的特征
圆柱由两个底面和一个侧面围成,两个底面是完全相等的两个圆形,侧面是一个曲面,展开后是一个长方形(或正方形)。
底面
侧面
底面
h
两个底面圆心之间的距离是圆柱的高。圆柱有无数条高。
高
复习回顾
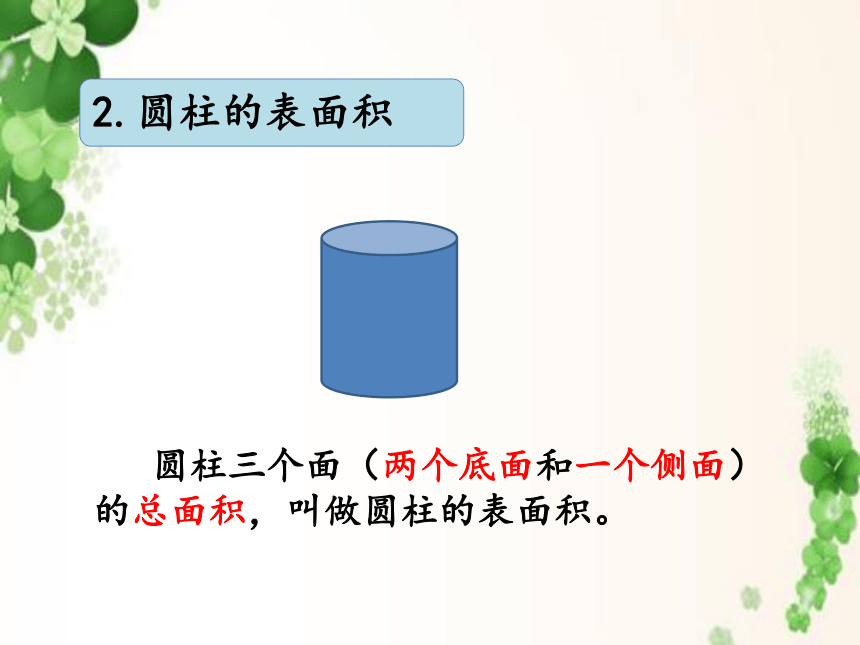
圆柱三个面(两个底面和一个侧面)的总面积,叫做圆柱的表面积。
2.圆柱的表面积
S侧
=
c
h
=
2πrh
高
底面周长
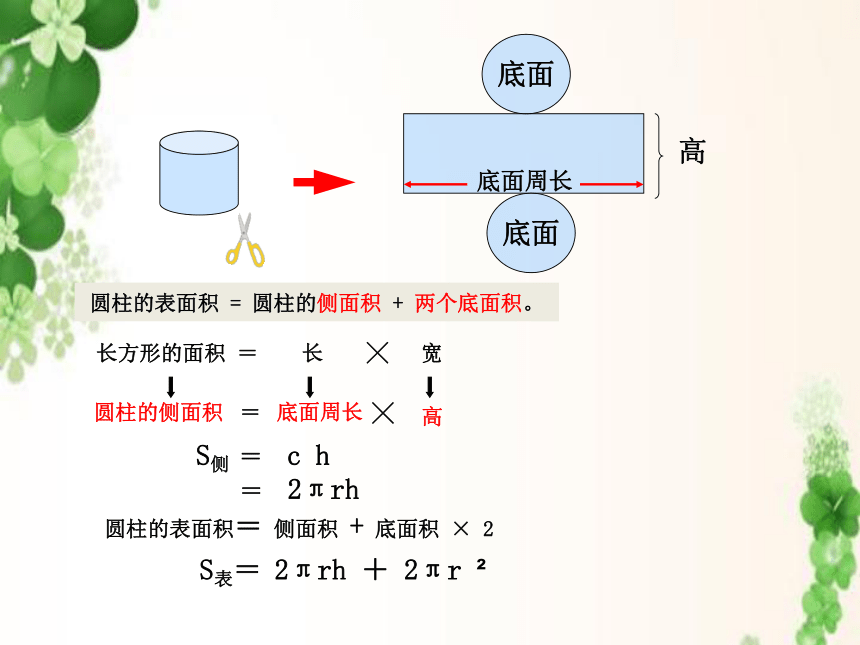
圆柱的表面积=
侧面积
+
底面积
×
2
S表=
2πrh
+
2πr
?
长方形的面积
=
长
╳
宽
圆柱的侧面积
底面周长
高
圆柱的表面积
=
圆柱的侧面积
+
两个底面积。
1.填空题。
(1)用一张边长是6厘米的正方形纸围成一个最大的圆柱形纸筒。这个纸筒的侧面积是(
)平方厘米。
(2)一个圆柱的底面积是12.56平方厘米,侧面积是62.8平方厘米,它的表面积是(
)平方厘米。
(3)一个圆柱的底面周长是6.28厘米,高是5厘米。它的侧面积是(
)平方厘米,表面积是(
)平方厘米。
36
87.92
31.4
37.68
6×6=36(平方厘米)
62.8+12.56×2=62.8+25.12=87.92(平方厘米)
6
.28×5=31.4(平方厘米)
半径:6.28÷3.14÷2=1(厘米)
表面积:31.4+3.14×1
?×2=31.4+6.28=37.68方厘米)
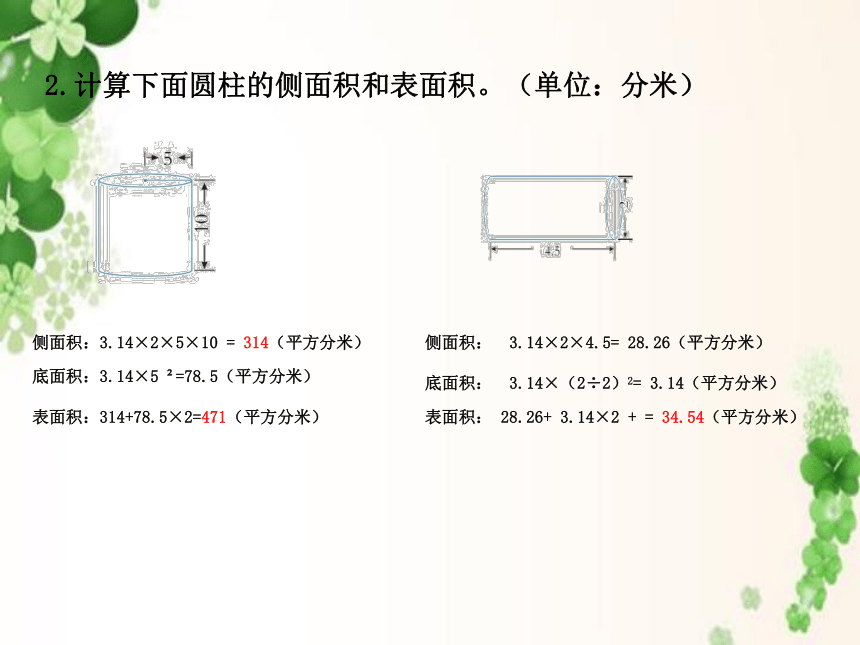
2.计算下面圆柱的侧面积和表面积。(单位:分米)
侧面积:3.14×2×5×10
=
314(平方分米)
底面积:3.14×5
?=78.5(平方分米)
表面积:314+78.5×2=471(平方分米)
侧面积:
3.14×2×4.5=
28.26(平方分米)
底面积:
3.14×(2÷2)2=
3.14(平方分米)
表面积:
28.26+
3.14×2
+
=
34.54(平方分米)
(1)做一个这样的圆柱形纸筒,至少需要多少平方分米的纸板?
底面积:
侧面积:
18.84
+
3.14×2
=25.12(平方分米)
表面积
=
侧面积
+
底面积
×
2
3.14×2×3
=18.84(平方分米)
3.14×(2÷2)?=3.14(平方分米)
答:做一个这样的圆柱形纸筒,至少需要25.12平方分米的纸板。
3.解决问题。
(2)一个鱼缸的侧面是用钢化玻璃制成的。制作这样一个鱼缸,至少需要多少平方米的钢化玻璃?
侧面积:3.14×2×3=18.84(平方米)
答:至少需要18.84平方米的钢化玻璃。
(3)一台压路机的前轮是圆柱形,轮宽2米,直径为1米。
①前轮滚动一周,压过的路面是多少平方米?
②如果每分钟滚动10周,压过的路面是多少平方米?
①侧面积:3.14×1×2=6.28(平方米)
答:压过的路面是6.28平方米。
②
6.28×10=62.8(平方米)
答:压过的路面是62.8平方米。
分析:求滚筒转一周可压路多少平方米?实际就是求圆柱的侧面积。宽是2米,也就是圆柱的高是2米。
(4)制作10个这样的手提包需要多少布料?
侧面积:3.14×20×50
=
3140(平方厘米)
表面积:2×314+3140=3768(平方厘米)
底面积:3.14×(20÷2)2=
314(平方厘米)
10个的表面积:3768×10=37680(平方厘米)
答:制作10个这样的手提包需要37680平方厘米布料。
(5)张杰在看了《极限挑战》有关垃圾分类的这一期节目后,他打算用硬纸板做5个圆柱形无盖小垃圾桶。他至少要准备多少平方米硬纸板?
侧面积:3.14×20×40
=
2512(平方厘米)
表面积:2512+314=2816(平方厘米)
底面积:3.14×(20÷2)2=
314(平方厘米)
5个的表面积:2816×5=14130(平方厘米)
=1.143(平方米)
答:他至少要准备1.143平方米硬纸板。
课堂总结
这节课我们一起复习了怎样求圆柱的侧面积和表面积,希望大家能在生活中学以致用。
完成《圆柱的表面积》复习诊断题。
课后作业
《圆柱的表面积》整理复习
1.圆柱的特征
圆柱由两个底面和一个侧面围成,两个底面是完全相等的两个圆形,侧面是一个曲面,展开后是一个长方形(或正方形)。
底面
侧面
底面
h
两个底面圆心之间的距离是圆柱的高。圆柱有无数条高。
高
复习回顾
圆柱三个面(两个底面和一个侧面)的总面积,叫做圆柱的表面积。
2.圆柱的表面积
S侧
=
c
h
=
2πrh
高
底面周长
圆柱的表面积=
侧面积
+
底面积
×
2
S表=
2πrh
+
2πr
?
长方形的面积
=
长
╳
宽
圆柱的侧面积
底面周长
高
圆柱的表面积
=
圆柱的侧面积
+
两个底面积。
1.填空题。
(1)用一张边长是6厘米的正方形纸围成一个最大的圆柱形纸筒。这个纸筒的侧面积是(
)平方厘米。
(2)一个圆柱的底面积是12.56平方厘米,侧面积是62.8平方厘米,它的表面积是(
)平方厘米。
(3)一个圆柱的底面周长是6.28厘米,高是5厘米。它的侧面积是(
)平方厘米,表面积是(
)平方厘米。
36
87.92
31.4
37.68
6×6=36(平方厘米)
62.8+12.56×2=62.8+25.12=87.92(平方厘米)
6
.28×5=31.4(平方厘米)
半径:6.28÷3.14÷2=1(厘米)
表面积:31.4+3.14×1
?×2=31.4+6.28=37.68方厘米)
2.计算下面圆柱的侧面积和表面积。(单位:分米)
侧面积:3.14×2×5×10
=
314(平方分米)
底面积:3.14×5
?=78.5(平方分米)
表面积:314+78.5×2=471(平方分米)
侧面积:
3.14×2×4.5=
28.26(平方分米)
底面积:
3.14×(2÷2)2=
3.14(平方分米)
表面积:
28.26+
3.14×2
+
=
34.54(平方分米)
(1)做一个这样的圆柱形纸筒,至少需要多少平方分米的纸板?
底面积:
侧面积:
18.84
+
3.14×2
=25.12(平方分米)
表面积
=
侧面积
+
底面积
×
2
3.14×2×3
=18.84(平方分米)
3.14×(2÷2)?=3.14(平方分米)
答:做一个这样的圆柱形纸筒,至少需要25.12平方分米的纸板。
3.解决问题。
(2)一个鱼缸的侧面是用钢化玻璃制成的。制作这样一个鱼缸,至少需要多少平方米的钢化玻璃?
侧面积:3.14×2×3=18.84(平方米)
答:至少需要18.84平方米的钢化玻璃。
(3)一台压路机的前轮是圆柱形,轮宽2米,直径为1米。
①前轮滚动一周,压过的路面是多少平方米?
②如果每分钟滚动10周,压过的路面是多少平方米?
①侧面积:3.14×1×2=6.28(平方米)
答:压过的路面是6.28平方米。
②
6.28×10=62.8(平方米)
答:压过的路面是62.8平方米。
分析:求滚筒转一周可压路多少平方米?实际就是求圆柱的侧面积。宽是2米,也就是圆柱的高是2米。
(4)制作10个这样的手提包需要多少布料?
侧面积:3.14×20×50
=
3140(平方厘米)
表面积:2×314+3140=3768(平方厘米)
底面积:3.14×(20÷2)2=
314(平方厘米)
10个的表面积:3768×10=37680(平方厘米)
答:制作10个这样的手提包需要37680平方厘米布料。
(5)张杰在看了《极限挑战》有关垃圾分类的这一期节目后,他打算用硬纸板做5个圆柱形无盖小垃圾桶。他至少要准备多少平方米硬纸板?
侧面积:3.14×20×40
=
2512(平方厘米)
表面积:2512+314=2816(平方厘米)
底面积:3.14×(20÷2)2=
314(平方厘米)
5个的表面积:2816×5=14130(平方厘米)
=1.143(平方米)
答:他至少要准备1.143平方米硬纸板。
课堂总结
这节课我们一起复习了怎样求圆柱的侧面积和表面积,希望大家能在生活中学以致用。
完成《圆柱的表面积》复习诊断题。
课后作业
