人教版数学七年级下册7.1平面直角坐标系讲义无答案
文档属性
| 名称 | 人教版数学七年级下册7.1平面直角坐标系讲义无答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 648.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 00:00:00 | ||
图片预览

文档简介
【教学标题】平面直角坐标系
【教学内容】
第一课时
有序数对
一、新课指引
在建国60周年的庆典活动中,天安门广场上出现了壮丽的背景图案,你知道它是怎样组成的吗?
二、看图答题
请你在图中标出下列座位的同学:(1,5),(2,4),(4,2),(3,3),(5,6)。
通过观察,你有什么发现?结合课本请归纳出“有序数对”的概念。
有序数对:
我们把这种有
的
个数a与b组成的数对,叫做有序数对,记作
。利用有序数对,可以很准确地表示出一个位置。
闯关训练
1.如图1所示,一方队正沿箭头所指的方向前进,
A的位置为三列四行(排),表示为(3,4),那么B
的位置是
(
)
A.(4,5)
B.(5,4)
C.(4,2)
D.(4,3)
2.如图1所示,B左侧第二个人的位置是
(
)
A.(2,5)
B.(5,2)
C.(2,2)
D.(5,5)
3.如图1所示,如果队伍向北前进,那么A(3,4)西侧第二个人的位置是
(
)
A.(4,1)
B.(1,4)
C.(1,3)
D.(3,1)
4.如图1所示,(4,3)表示的位置是
(
)
A.A
B.B
C.C
D.D
5.如图所示A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?
基础知识达标
1.海口、北京的位置用东经和北纬的度数应怎样表示成有序数对?
2.如图1,商场六楼点A的位置可表示为(6,1,2),那么五楼点B的位置可表示为
,二楼点C
的位置可表示为
。
3.如图2,该图是用黑白两种颜色的若干棋子在方格纸上摆出的两幅图案,如果用(0,0)表示A点位置,用(2,1)表示B点的位置,那么图中五枚黑棋的位置是:C
,
D
,
E
,
F
,
G
。
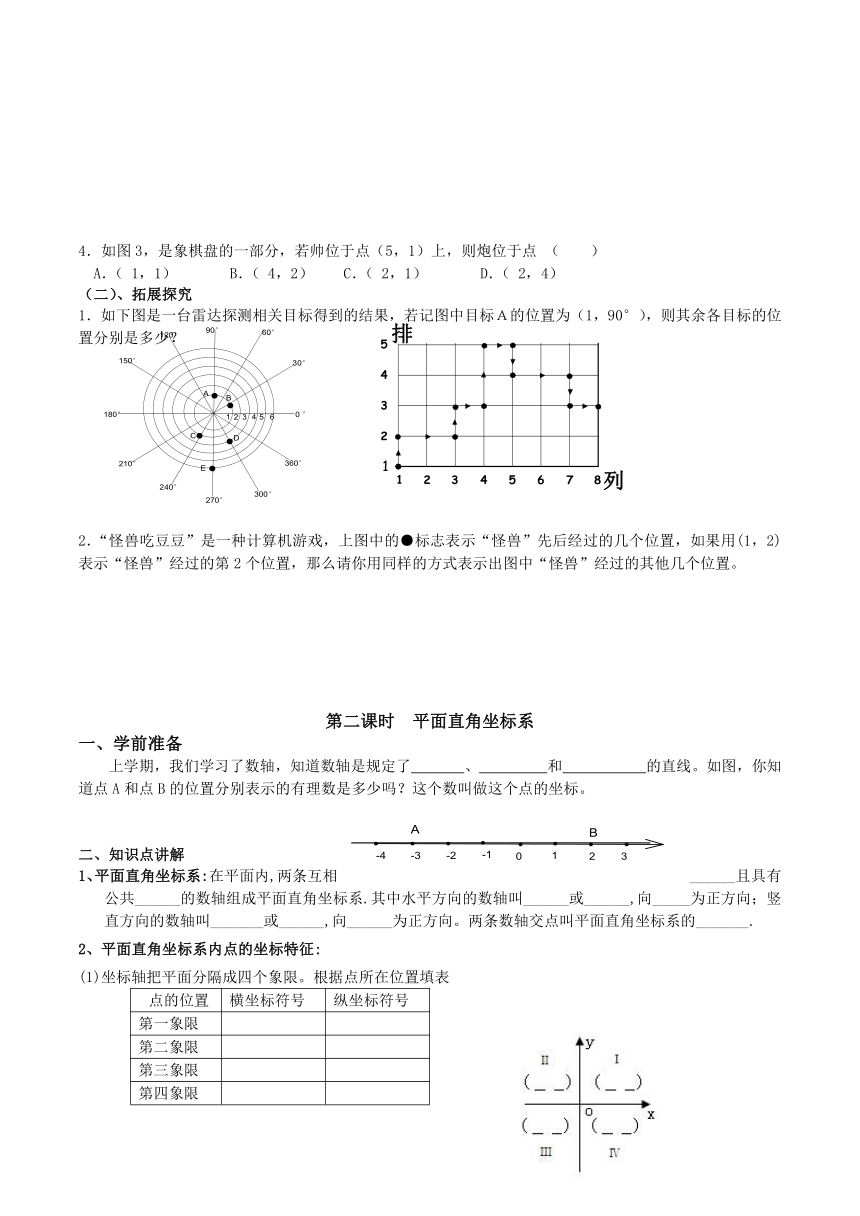
4.如图3,是象棋盘的一部分,若帅位于点(5,1)上,则炮位于点
(
)
A.(
1,1)
B.(
4,2)
C.(
2,1)
D.(
2,4)
(二)、拓展探究
1.如下图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(1,90°),则其余各目标的位置分别是多少?
2.“怪兽吃豆豆”是一种计算机游戏,上图中的●标志表示“怪兽”先后经过的几个位置,如果用(1,2)表示“怪兽”经过的第2个位置,那么请你用同样的方式表示出图中“怪兽”经过的其他几个位置。
第二课时
平面直角坐标系
一、学前准备
上学期,我们学习了数轴,知道数轴是规定了
、
和
的直线。如图,你知道点A和点B的位置分别表示的有理数是多少吗?这个数叫做这个点的坐标。
二、知识点讲解
1、平面直角坐标系:在平面内,两条互相______且具有公共______的数轴组成平面直角坐标系.其中水平方向的数轴叫______或______,向_____为正方向;竖直方向的数轴叫_______或______,向______为正方向。两条数轴交点叫平面直角坐标系的_______.
2、平面直角坐标系内点的坐标特征:
(1)坐标轴把平面分隔成四个象限。根据点所在位置填表
点的位置
横坐标符号
纵坐标符号
第一象限
第二象限
第三象限
第四象限
(2)坐标轴上的点不属于任何象限,它们的坐标特征
在x轴上的点______坐标为0;
在y轴上的点______坐标为0;
(3)P(a,b)关于x轴、y轴、原点的对称点坐标特征
点P(a,b)关于x轴对称点P1_____________
;
点
P(a,b)关于y轴对称点P2_____________
;
点P(a,b)关于原点对称点P3_____________
。
3、平行于x轴的直线上的点______坐标相同;平行于y轴的直线上的点_______坐标相同.
自我挑战:
1.如图A点坐标为(4,5),请你在坐标图中描出下列各点:B(-2,3),C(-4,-1),D(2.5,-2),E(0,4),F(3,0)。
2.写出图中的多边形ABCDEF各个顶点的坐标。
A(
,
)
B(
,
)
C(
,
)
D(
,
)E
(
,
)F(
,
)。
如:若以线段BC所在的直线为x轴,纵轴(y轴)位置不变,
则六个顶点的坐标分别为:A(__,__),B(__,__),C(___,__),
D(__,___),E(___,__),F(__,__)。
3.点A(2,7)到x轴的距离为
,到y轴的距离为
;
4.若点P(a,b)在第四象限内,则a,b的取值范围是(
)
A、a>0,b<0
B、a>0,b>0
C、a<0,b>0
D、a<0,b<0
5.如图,在平面直角坐标系中表示下面各点:
A(0,3);
B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);
G(5,0)
;H(-3,5)
(1)A点到原点O的距离是
;
(2)将点C向轴的负方向平移6个单位,
它与点
重合;
(3)连接CE,则直线CE与轴是什么关系?
(4)点F分别到、轴的距离是多少?
(5)观察点C与点E横纵坐标与位置的特点;
(6)观察点C与点H横纵坐标与位置的特点;
(7)观察点C与点D横纵坐标与位置的特点。
【过手练习】
1.点A(-2,3)到x轴的距离为
,到y轴的距离是
。
2.x轴上有A、B两点,A点坐标为(3,0),A、B之间的距离为5,则B点坐标为
。
3.若点N(a+5,a-2)在y轴上,则a=
,N点的坐标为
。
4.如果点A(x,y)在第三象限,则点B(-x,y-1)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.点P在y轴左方、x轴上方,距y轴、x轴分别为3、4个单位长度,点P的坐标是(
)
A.(3,-4)
B.(-3,4)
C.(4,-3)
D.(-4,3)
6.已知点P(x,y)在第二象限,且,则点P的坐标为(
)
A.(-2,3)
B.(2,-3)
C.(-3,2)
D.(2,3)
7.如图,点A的坐标为(-3,4)。(1)写出图中点B、C、D、E、
F、G、H的坐标,并观察点A和C,点B和D有什么关系?
(2)在图中标出(-2,4)、(5,5)、(4,-3)三点的位置。
【拓展训练】
已知点P(2,3)。(1)在坐标平面内画出点P;(2)分别求出点P关于x轴、y轴的对称点P1、P2.?(3)求三角形P1PP2的面积。
图1
图1
_
B
_
A
_
C
_
D
_
E
_
G
_
F
图(2)
图2
图3
图(1)
1
【教学内容】
第一课时
有序数对
一、新课指引
在建国60周年的庆典活动中,天安门广场上出现了壮丽的背景图案,你知道它是怎样组成的吗?
二、看图答题
请你在图中标出下列座位的同学:(1,5),(2,4),(4,2),(3,3),(5,6)。
通过观察,你有什么发现?结合课本请归纳出“有序数对”的概念。
有序数对:
我们把这种有
的
个数a与b组成的数对,叫做有序数对,记作
。利用有序数对,可以很准确地表示出一个位置。
闯关训练
1.如图1所示,一方队正沿箭头所指的方向前进,
A的位置为三列四行(排),表示为(3,4),那么B
的位置是
(
)
A.(4,5)
B.(5,4)
C.(4,2)
D.(4,3)
2.如图1所示,B左侧第二个人的位置是
(
)
A.(2,5)
B.(5,2)
C.(2,2)
D.(5,5)
3.如图1所示,如果队伍向北前进,那么A(3,4)西侧第二个人的位置是
(
)
A.(4,1)
B.(1,4)
C.(1,3)
D.(3,1)
4.如图1所示,(4,3)表示的位置是
(
)
A.A
B.B
C.C
D.D
5.如图所示A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?
基础知识达标
1.海口、北京的位置用东经和北纬的度数应怎样表示成有序数对?
2.如图1,商场六楼点A的位置可表示为(6,1,2),那么五楼点B的位置可表示为
,二楼点C
的位置可表示为
。
3.如图2,该图是用黑白两种颜色的若干棋子在方格纸上摆出的两幅图案,如果用(0,0)表示A点位置,用(2,1)表示B点的位置,那么图中五枚黑棋的位置是:C
,
D
,
E
,
F
,
G
。
4.如图3,是象棋盘的一部分,若帅位于点(5,1)上,则炮位于点
(
)
A.(
1,1)
B.(
4,2)
C.(
2,1)
D.(
2,4)
(二)、拓展探究
1.如下图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(1,90°),则其余各目标的位置分别是多少?
2.“怪兽吃豆豆”是一种计算机游戏,上图中的●标志表示“怪兽”先后经过的几个位置,如果用(1,2)表示“怪兽”经过的第2个位置,那么请你用同样的方式表示出图中“怪兽”经过的其他几个位置。
第二课时
平面直角坐标系
一、学前准备
上学期,我们学习了数轴,知道数轴是规定了
、
和
的直线。如图,你知道点A和点B的位置分别表示的有理数是多少吗?这个数叫做这个点的坐标。
二、知识点讲解
1、平面直角坐标系:在平面内,两条互相______且具有公共______的数轴组成平面直角坐标系.其中水平方向的数轴叫______或______,向_____为正方向;竖直方向的数轴叫_______或______,向______为正方向。两条数轴交点叫平面直角坐标系的_______.
2、平面直角坐标系内点的坐标特征:
(1)坐标轴把平面分隔成四个象限。根据点所在位置填表
点的位置
横坐标符号
纵坐标符号
第一象限
第二象限
第三象限
第四象限
(2)坐标轴上的点不属于任何象限,它们的坐标特征
在x轴上的点______坐标为0;
在y轴上的点______坐标为0;
(3)P(a,b)关于x轴、y轴、原点的对称点坐标特征
点P(a,b)关于x轴对称点P1_____________
;
点
P(a,b)关于y轴对称点P2_____________
;
点P(a,b)关于原点对称点P3_____________
。
3、平行于x轴的直线上的点______坐标相同;平行于y轴的直线上的点_______坐标相同.
自我挑战:
1.如图A点坐标为(4,5),请你在坐标图中描出下列各点:B(-2,3),C(-4,-1),D(2.5,-2),E(0,4),F(3,0)。
2.写出图中的多边形ABCDEF各个顶点的坐标。
A(
,
)
B(
,
)
C(
,
)
D(
,
)E
(
,
)F(
,
)。
如:若以线段BC所在的直线为x轴,纵轴(y轴)位置不变,
则六个顶点的坐标分别为:A(__,__),B(__,__),C(___,__),
D(__,___),E(___,__),F(__,__)。
3.点A(2,7)到x轴的距离为
,到y轴的距离为
;
4.若点P(a,b)在第四象限内,则a,b的取值范围是(
)
A、a>0,b<0
B、a>0,b>0
C、a<0,b>0
D、a<0,b<0
5.如图,在平面直角坐标系中表示下面各点:
A(0,3);
B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);
G(5,0)
;H(-3,5)
(1)A点到原点O的距离是
;
(2)将点C向轴的负方向平移6个单位,
它与点
重合;
(3)连接CE,则直线CE与轴是什么关系?
(4)点F分别到、轴的距离是多少?
(5)观察点C与点E横纵坐标与位置的特点;
(6)观察点C与点H横纵坐标与位置的特点;
(7)观察点C与点D横纵坐标与位置的特点。
【过手练习】
1.点A(-2,3)到x轴的距离为
,到y轴的距离是
。
2.x轴上有A、B两点,A点坐标为(3,0),A、B之间的距离为5,则B点坐标为
。
3.若点N(a+5,a-2)在y轴上,则a=
,N点的坐标为
。
4.如果点A(x,y)在第三象限,则点B(-x,y-1)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.点P在y轴左方、x轴上方,距y轴、x轴分别为3、4个单位长度,点P的坐标是(
)
A.(3,-4)
B.(-3,4)
C.(4,-3)
D.(-4,3)
6.已知点P(x,y)在第二象限,且,则点P的坐标为(
)
A.(-2,3)
B.(2,-3)
C.(-3,2)
D.(2,3)
7.如图,点A的坐标为(-3,4)。(1)写出图中点B、C、D、E、
F、G、H的坐标,并观察点A和C,点B和D有什么关系?
(2)在图中标出(-2,4)、(5,5)、(4,-3)三点的位置。
【拓展训练】
已知点P(2,3)。(1)在坐标平面内画出点P;(2)分别求出点P关于x轴、y轴的对称点P1、P2.?(3)求三角形P1PP2的面积。
图1
图1
_
B
_
A
_
C
_
D
_
E
_
G
_
F
图(2)
图2
图3
图(1)
1
