人教版数学八年级下册第十七章 勾股定理复习巩固教案
文档属性
| 名称 | 人教版数学八年级下册第十七章 勾股定理复习巩固教案 |  | |
| 格式 | zip | ||
| 文件大小 | 323.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 12:03:17 | ||
图片预览



文档简介
勾股定理巩固教案
【教学目标】
了解勾股定理的定义、作用,能够验证勾股定理
学会勾股定理的逆定理,证明直角三角形
通过勾股定理,解直角三角形
【重点难点】
勾股定理的逆定理,证明直角三角形
通过勾股定理,解直角三角形
【教学内容】
知识要点总结
1.勾股定理:直角三角形两直角边的平方和等于斜边的平方。
即。
2.勾股定理的逆定理是判别一个三角形为直角三角形常用的方法。若三角形的三边长a,b,c满足,则这个三角形是直角三角形。
利用勾股定理的逆定理判别直角三角形的一般步骤:
①先找出最大边(如c)
②计算与,并验证是否相等。
若=,则△ABC是直角三角形。
若≠,则△ABC不是Rt△。
3.
若a、b、c均为自然数,且无1以外的整数公因式当它们满足关系式时,我们称(a、b、c)为基本勾股数组。记一记:
,,,,,,…均为基本勾股数组。
4.作长为的线段(以为例)
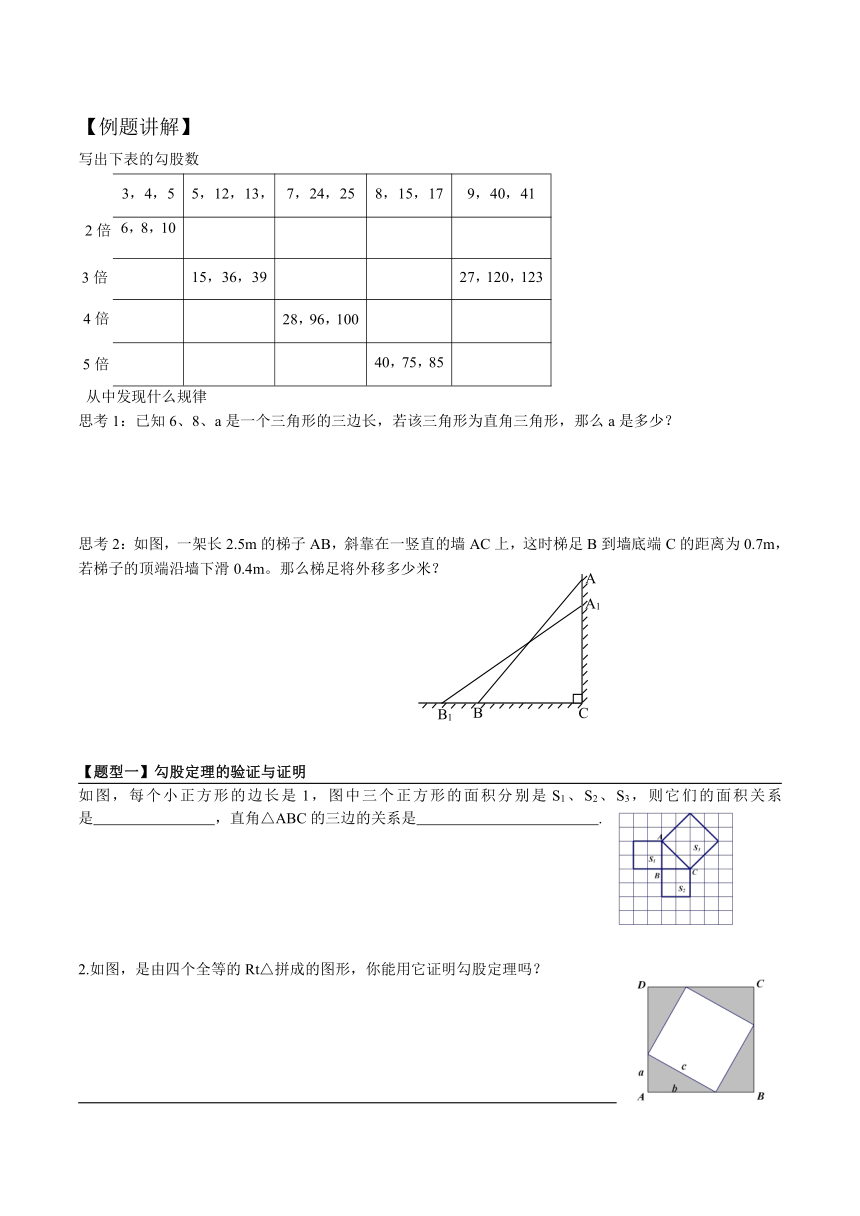
【例题讲解】
写出下表的勾股数
3,4,5
5,12,13,
7,24,25
8,15,17
9,40,41
6,8,10
15,36,39
27,120,123
28,96,100
40,75,85
从中发现什么规律
思考1:已知6、8、a是一个三角形的三边长,若该三角形为直角三角形,那么a是多少?
思考2:如图,一架长2.5m的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7m,若梯子的顶端沿墙下滑0.4m。那么梯足将外移多少米?
【题型一】勾股定理的验证与证明
如图,每个小正方形的边长是1,图中三个正方形的面积分别是S1、S2、S3,则它们的面积关系是 ,直角△ABC的三边的关系是 .
2.如图,是由四个全等的Rt△拼成的图形,你能用它证明勾股定理吗?
3.如图,已知∠A=∠B=90°且△AED≌△BCE,A、E、B在同一直线上.根据此图证明勾股定理.
【题型二】以勾股定理为基础的有趣结论
1.如图,直线l上有三个正方形a、b、c若a和c的面积分别为5和11,则b的面积为多少?
【题型三】利用勾股定理求边长和进行论证
1.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为(
)
A.3
B.4
C.5
D.
2.在Rt△ABC中,∠C=90°,∠B=45°,c=10,则a的长为(
)
A.5
B.
C.
D.
3.等边三角形的边长为2,则该三角形的面积为(
)
A.
B.
C.
D.3
4.若等腰三角形的腰长为10,底边长为12,则底边上的高为(
)
A.6
B.7
C.8
D.9
5.若一个三角形的三边长为3、4、x,则使此三角形是直角三角形的x的值是(
)
A.5
B.
6
C.
D.5或
6.将直角三角形的三边扩大相同的倍数后,得到的三角形是(
)
A
直角三角形
B
锐角三角形
C
钝角三角形
D
不能确定
7.如图是一张直角三角形的纸片,两直角边AC=6
cm、BC=8
cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4
cm
B.5
cm
C.6
cm
D.10
cm
8.
将一个有45度角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30度角,如图,则三角板的最大边的长为( )
A.
3cm
B.
6cm
C.
3cm
D.
6cm
9.
如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5
B.4.2
C.5.8
D.7
【题型四】勾股定理在非直角三角形中的应用
1.若△ABC中,,高AD=12,则BC的长为(
)
A、14
B、4
C、14或4
D、以上都不对
2.已知:如图,在△ABC中,AB=15,BC=14,AC=13.求△ABC的面积.
【题型五】利用勾股定理求不规则图形的面积
1.如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.
求四边形ABCD的面积和AD,BC的长。
.四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26.求四边形ABCD的面积.
【题型六】勾股定理与方程(组)
2.已知Rt△ABC中,∠C=90°,a+b=14,c=10,则Rt△ABC的面积是(
)
A.24
B.36
C.48
D.60
3.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A.56
B.48
C.40
D.32
4.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为(
)cm2.
A.
6
B.
8
C.
10
D.
12
【解答题】
1.已知,如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=1.5,BD=2.5,求AC的长.
2.如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得树顶端A的仰角为30°,已知侧角仪高DC=1.4m,BC=30米,请帮助小明计算出树高AB.(
【题型七】利用勾股定理求最值
1.如图,长方体的长为15,宽为10,高为20,点离点的距离为5,一只蚂蚁如果要沿着长方体的表面从点爬到点,需要爬行的最短距离是( )
A.
B.25
C.
D.
2.
如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
【题型八】勾股定理逆定理及其应用
1.分别以下列四组为一个三角形的三边的长:①6、8、10;②5、12、13;③8、15、17;
④7、8、9,其中能构成直角三角形的有(
).
A.4组
B.3组
C.2组
D.1组
2.满足下列条件的三角形中,不是直角三角形的是(
)
A.三个内角比为1∶2∶1
B.三边之比为1∶2∶
C.三边之比为∶2∶
D.
三个内角比为1∶2∶3
3.已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为(
)
A.
B.
C.
D.以上都不对
4.三角形的三边
a、b、c满足关系:(a十b)2=c2
+2ab,则这个三角形是(
)
A.直角三角形
B、锐角三角形
C.钝角三角形
D条件不足,不能确定
5.若△ABC的三边a、b、c满足a2+b2+c2十338=10a+24b+26c,则△ABC的面积是( )
A.338 B.24 C.26 D.30
【题型九】勾股定理及逆定理与实际问题
1.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要
(
).
A.17m
B.18m
C.25m
D.26m
2.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是(
).
A.h≤17cm
B.h≥8cm
C.15cm≤h≤16cm
D.7cm≤h≤16cm
3.如图1,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5m,梯子滑动后停在DE的位置上,如图2,测得BD长为0.5m,求梯子顶端A下落了多少米.
考点直击
考点一:已知两边求第三边
1.直角三角形中,以直角边为边长的两个正方形的面积为7,8,则以斜边为边长的正方形的面积为_________.
2、已知直角三角形的两边长为3、2,则另一条边长是________________.
3、在数轴上作出表示的点.
4、一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
考点二:求线段的长
1.把一根长为10㎝的铁丝弯成一个直角三角形的两条直角边,如果要使三角形的面积是9㎝2,那么还要准备一根长为____的铁丝才能把三角形做好.
2.如图,将一个边长分别为4、8的长方形纸片ABCD折
叠,使C点与A点重合,则EB的长是(
).
A.3
B.4
C.
D.5
3.如图,铁路上A,B两点相距25km,C,D为两村庄,
DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
考点三、判别一个三角形是否是直角三角形(勾股定理逆定理的应用)
1.若△ABC的三个外角的度数之比为3:4:5,最大边AB与最小边BC的关系是_________.
2.若一个三角形的周长12cm,一边长为3cm,其他两边之差为cm,则这个三角形
是______________________.
3.将直角三角形的三边扩大相同的倍数后,得到的三角形是
(
).
A.直角三角形
B.锐角三角形
C.钝角三角形
D.不是直角三角形
4.下列命题中是假命题的是(
).
A.△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形.
B.△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形.
C.△ABC中,若∠A∶∠B∶∠C=3∶4∶5则△ABC是直角三角形.
D.△ABC中,若a∶b∶c=5∶4∶3则△ABC是直角三角形.
5.在△ABC中,,那么△ABC是(?
).
????
A.等腰三角形?????
B.钝角三角形?????
C.直角三角形????
D.等腰直角三角形
6.如图,四边形ABCD中,F为DC的中点,E为BC上一点,
且.你能说明∠AFE是直角吗?
考点四、开放型试题
1.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_______.
2、图示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,和2′,…,依次类推,若正方形7的边长为1cm,则正方形1的边长为__________cm.
五、课后练习
1、小杨从学校出发向南走150米,接着向东走了360米到九龙山商场,学校与九龙山商场的距离是
米.
2、如图:带阴影部分的半圆的面积是多少?(取3)
3、已知直角三角形两直角边长分别为5和12,
求斜边上的高.
4、
如图∠B=90?,AB=16cm,BC=12cm,AD=21cm,CD=29cm
求四边形ABCD的面积.
5、在加工如图的垫模时,请根据图中的尺寸,求垫模中AB间的尺寸.
a
b
c
1
1
1
1
1
x
y
1
2
0
2倍
3倍
4倍
5倍
A
A1
B1
B
C
5
20
15
10
C
A
B
A
D
E
B
C
6
8
1
【教学目标】
了解勾股定理的定义、作用,能够验证勾股定理
学会勾股定理的逆定理,证明直角三角形
通过勾股定理,解直角三角形
【重点难点】
勾股定理的逆定理,证明直角三角形
通过勾股定理,解直角三角形
【教学内容】
知识要点总结
1.勾股定理:直角三角形两直角边的平方和等于斜边的平方。
即。
2.勾股定理的逆定理是判别一个三角形为直角三角形常用的方法。若三角形的三边长a,b,c满足,则这个三角形是直角三角形。
利用勾股定理的逆定理判别直角三角形的一般步骤:
①先找出最大边(如c)
②计算与,并验证是否相等。
若=,则△ABC是直角三角形。
若≠,则△ABC不是Rt△。
3.
若a、b、c均为自然数,且无1以外的整数公因式当它们满足关系式时,我们称(a、b、c)为基本勾股数组。记一记:
,,,,,,…均为基本勾股数组。
4.作长为的线段(以为例)
【例题讲解】
写出下表的勾股数
3,4,5
5,12,13,
7,24,25
8,15,17
9,40,41
6,8,10
15,36,39
27,120,123
28,96,100
40,75,85
从中发现什么规律
思考1:已知6、8、a是一个三角形的三边长,若该三角形为直角三角形,那么a是多少?
思考2:如图,一架长2.5m的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7m,若梯子的顶端沿墙下滑0.4m。那么梯足将外移多少米?
【题型一】勾股定理的验证与证明
如图,每个小正方形的边长是1,图中三个正方形的面积分别是S1、S2、S3,则它们的面积关系是 ,直角△ABC的三边的关系是 .
2.如图,是由四个全等的Rt△拼成的图形,你能用它证明勾股定理吗?
3.如图,已知∠A=∠B=90°且△AED≌△BCE,A、E、B在同一直线上.根据此图证明勾股定理.
【题型二】以勾股定理为基础的有趣结论
1.如图,直线l上有三个正方形a、b、c若a和c的面积分别为5和11,则b的面积为多少?
【题型三】利用勾股定理求边长和进行论证
1.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为(
)
A.3
B.4
C.5
D.
2.在Rt△ABC中,∠C=90°,∠B=45°,c=10,则a的长为(
)
A.5
B.
C.
D.
3.等边三角形的边长为2,则该三角形的面积为(
)
A.
B.
C.
D.3
4.若等腰三角形的腰长为10,底边长为12,则底边上的高为(
)
A.6
B.7
C.8
D.9
5.若一个三角形的三边长为3、4、x,则使此三角形是直角三角形的x的值是(
)
A.5
B.
6
C.
D.5或
6.将直角三角形的三边扩大相同的倍数后,得到的三角形是(
)
A
直角三角形
B
锐角三角形
C
钝角三角形
D
不能确定
7.如图是一张直角三角形的纸片,两直角边AC=6
cm、BC=8
cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4
cm
B.5
cm
C.6
cm
D.10
cm
8.
将一个有45度角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30度角,如图,则三角板的最大边的长为( )
A.
3cm
B.
6cm
C.
3cm
D.
6cm
9.
如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5
B.4.2
C.5.8
D.7
【题型四】勾股定理在非直角三角形中的应用
1.若△ABC中,,高AD=12,则BC的长为(
)
A、14
B、4
C、14或4
D、以上都不对
2.已知:如图,在△ABC中,AB=15,BC=14,AC=13.求△ABC的面积.
【题型五】利用勾股定理求不规则图形的面积
1.如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.
求四边形ABCD的面积和AD,BC的长。
.四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26.求四边形ABCD的面积.
【题型六】勾股定理与方程(组)
2.已知Rt△ABC中,∠C=90°,a+b=14,c=10,则Rt△ABC的面积是(
)
A.24
B.36
C.48
D.60
3.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A.56
B.48
C.40
D.32
4.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为(
)cm2.
A.
6
B.
8
C.
10
D.
12
【解答题】
1.已知,如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=1.5,BD=2.5,求AC的长.
2.如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得树顶端A的仰角为30°,已知侧角仪高DC=1.4m,BC=30米,请帮助小明计算出树高AB.(
【题型七】利用勾股定理求最值
1.如图,长方体的长为15,宽为10,高为20,点离点的距离为5,一只蚂蚁如果要沿着长方体的表面从点爬到点,需要爬行的最短距离是( )
A.
B.25
C.
D.
2.
如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
【题型八】勾股定理逆定理及其应用
1.分别以下列四组为一个三角形的三边的长:①6、8、10;②5、12、13;③8、15、17;
④7、8、9,其中能构成直角三角形的有(
).
A.4组
B.3组
C.2组
D.1组
2.满足下列条件的三角形中,不是直角三角形的是(
)
A.三个内角比为1∶2∶1
B.三边之比为1∶2∶
C.三边之比为∶2∶
D.
三个内角比为1∶2∶3
3.已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为(
)
A.
B.
C.
D.以上都不对
4.三角形的三边
a、b、c满足关系:(a十b)2=c2
+2ab,则这个三角形是(
)
A.直角三角形
B、锐角三角形
C.钝角三角形
D条件不足,不能确定
5.若△ABC的三边a、b、c满足a2+b2+c2十338=10a+24b+26c,则△ABC的面积是( )
A.338 B.24 C.26 D.30
【题型九】勾股定理及逆定理与实际问题
1.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要
(
).
A.17m
B.18m
C.25m
D.26m
2.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是(
).
A.h≤17cm
B.h≥8cm
C.15cm≤h≤16cm
D.7cm≤h≤16cm
3.如图1,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5m,梯子滑动后停在DE的位置上,如图2,测得BD长为0.5m,求梯子顶端A下落了多少米.
考点直击
考点一:已知两边求第三边
1.直角三角形中,以直角边为边长的两个正方形的面积为7,8,则以斜边为边长的正方形的面积为_________.
2、已知直角三角形的两边长为3、2,则另一条边长是________________.
3、在数轴上作出表示的点.
4、一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
考点二:求线段的长
1.把一根长为10㎝的铁丝弯成一个直角三角形的两条直角边,如果要使三角形的面积是9㎝2,那么还要准备一根长为____的铁丝才能把三角形做好.
2.如图,将一个边长分别为4、8的长方形纸片ABCD折
叠,使C点与A点重合,则EB的长是(
).
A.3
B.4
C.
D.5
3.如图,铁路上A,B两点相距25km,C,D为两村庄,
DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
考点三、判别一个三角形是否是直角三角形(勾股定理逆定理的应用)
1.若△ABC的三个外角的度数之比为3:4:5,最大边AB与最小边BC的关系是_________.
2.若一个三角形的周长12cm,一边长为3cm,其他两边之差为cm,则这个三角形
是______________________.
3.将直角三角形的三边扩大相同的倍数后,得到的三角形是
(
).
A.直角三角形
B.锐角三角形
C.钝角三角形
D.不是直角三角形
4.下列命题中是假命题的是(
).
A.△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形.
B.△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形.
C.△ABC中,若∠A∶∠B∶∠C=3∶4∶5则△ABC是直角三角形.
D.△ABC中,若a∶b∶c=5∶4∶3则△ABC是直角三角形.
5.在△ABC中,,那么△ABC是(?
).
????
A.等腰三角形?????
B.钝角三角形?????
C.直角三角形????
D.等腰直角三角形
6.如图,四边形ABCD中,F为DC的中点,E为BC上一点,
且.你能说明∠AFE是直角吗?
考点四、开放型试题
1.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_______.
2、图示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,和2′,…,依次类推,若正方形7的边长为1cm,则正方形1的边长为__________cm.
五、课后练习
1、小杨从学校出发向南走150米,接着向东走了360米到九龙山商场,学校与九龙山商场的距离是
米.
2、如图:带阴影部分的半圆的面积是多少?(取3)
3、已知直角三角形两直角边长分别为5和12,
求斜边上的高.
4、
如图∠B=90?,AB=16cm,BC=12cm,AD=21cm,CD=29cm
求四边形ABCD的面积.
5、在加工如图的垫模时,请根据图中的尺寸,求垫模中AB间的尺寸.
a
b
c
1
1
1
1
1
x
y
1
2
0
2倍
3倍
4倍
5倍
A
A1
B1
B
C
5
20
15
10
C
A
B
A
D
E
B
C
6
8
1
