湘教版七年级数学下册课件:4.5垂线第2课时垂线段与点到直线的距离(共21张PPT)
文档属性
| 名称 | 湘教版七年级数学下册课件:4.5垂线第2课时垂线段与点到直线的距离(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
4.5
垂线
第2课时
垂线段与点到直线的距离
湘教版
七年级下册
1.理解垂线的画法;
2.
知道垂线段和点到直线的距离的概念,并会应用解决问题.
(重点、难点)
学习目标
思考:在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
情境引入
思考:在平面内,通过一点能不能画一条直线与已知直线垂直?如果可能,能够画几条?
把l
所在的纸片在P点折叠过来,使射线PB与PA重合,折痕是直线PM,如图,由于∠1=∠2,且∠1+∠2=______,所以∠1=∠2=_________,因此PM是过点P且垂直l的直线.
A
B
P
l
A
B
P
l
1
2
M
(1)如图,设P点在直线l上.
180°
90°
推进新课
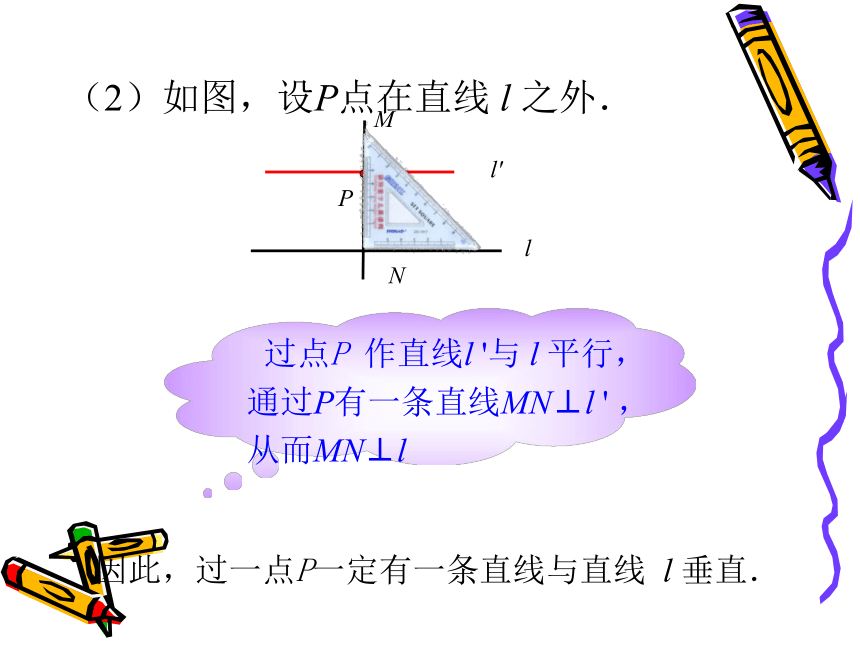
(2)如图,设P点在直线
l
之外.
过点P
作直线l
'与
l
平行,通过P有一条直线MN⊥l
'
,从而MN⊥l
l
M
N
l'
P
因此,过一点P一定有一条直线与直线
l
垂直.
(1)
讨论:平面内过一点P能够有两条或两条以上的直线与直线
l
垂直吗?
在平面内,通过一点有一条且只有一条直线与已知直线垂直.
(2)
如果直线PC与PD都与l垂直,那么PC与PD的位置关系合怎样?
有且只能有一条
会重合
P
C
D
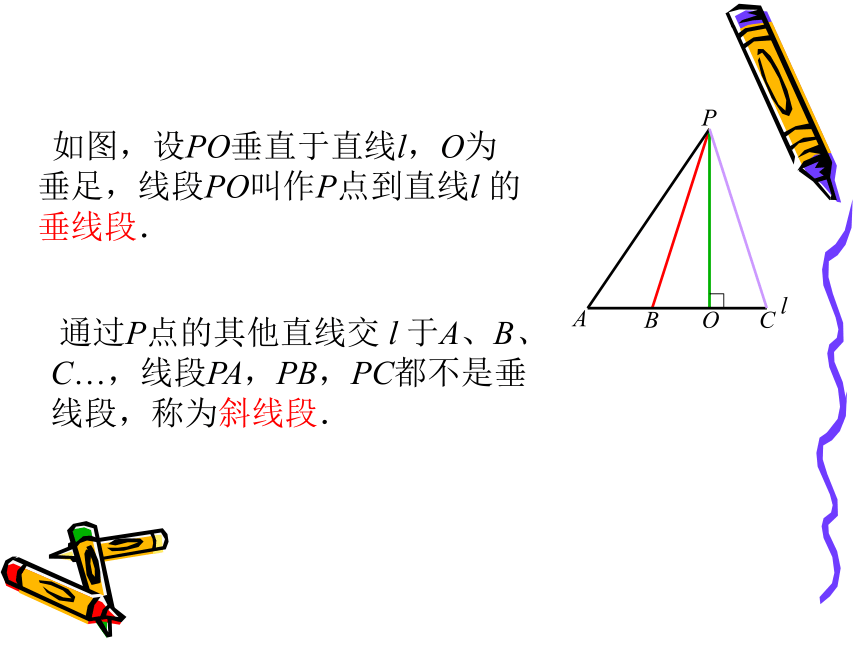
如图,设PO垂直于直线l,O为垂足,线段PO叫作P点到直线l
的垂线段.
P
B
l
O
A
C
通过P点的其他直线交
l
于A、B、
C…,线段PA,PB,PC都不是垂线段,称为斜线段.
(1)
如图,设P是直线l
外的一点,其细线一根,一端用图钉固定在P点,将细线拉直使它与l
垂直,在垂足O处作一标志,然后拉紧细线左右旋转至PA,PB等位置,比较PO,PA,PB的长度,你能从中猜出什么结论?
根据操作,我们不难猜想,所有这些线段中,垂线段PO最短.
p
O
这个猜想对吗?为什么?
(2)
用小纸片剪一个和三角形POB一样的三角形盖在三角形POB上,将纸片沿直线l翻折过来,得到三角形P'OB,
P
P'
B
O
l
或者简单地说成:
直线外一点与直线上各点连结的所有线段中,垂线段最短
这个猜想对吗?为什么?
如图,因为∠POB=∠P'OB=90?,所以POP'成一直线段,于是PO+P'O垂线段最短.
在图中,垂线段PO的长度点到直线
l
的距离.
练习:如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
C
∟
垂线段最短
N
1.如图所示,某工厂要在河岸
l
上建一个水泵房引水到C处,问建在哪个位置上才最节省水管?为什么?
l
C
由C点向l作垂线,CP,垂足为P,所以建在P点上最节省水管.
P
垂线段最短
如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为D,AB=5,BC=12,AC=13.
求:(1)点A到BC的距离;
(2)点B到直线AC的距离.
A
D
C
B
解:(1)因为∠ABC=90°,
所以AB⊥BC,B为垂足.
所以线段AB即为点A到直线BC的垂线段.
因为AB=5,
所以点A到直线BC的距离为5.
(2)因为BD⊥AC,垂足为D,
所以线段BD的长度即为点B到直线AC的距离.
1.过点P
向线段AB
所在直线引垂线,正确的是(
)
A
B
C
D
C
当堂练习
2.如图,
AC⊥BC,
∠C=90°
,线段AC、BC、CD中最短
的是
(
)
A.
AC
B.
BC
C.
CD
D.
不能确定
D
A
B
C
C
3.
P
是直线
AB
外一点,过点
P
作
PO⊥AB
,垂足为
O
,若
C
为直线
AB
上任意一点,则线段
PC
与线段
PO
的大小关系是(
)
A.
PC
>
PO
B.
PC
<
PO
C.
PC
≥
PO
D.
PC
≤
PO
C
4.下列说法正确的是(
)
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
A
B
C
D
D
5.一辆汽车在直线形的公路AB上由A向B行驶,C、D
是分别位于公路AB两侧的加油站.
(1)设汽车行驶到公路AB上点M的位置时,距离加油站C最近;行驶到点N的位置时,距离加油站D最近,请在图中分别画出点M、N的位置;
A
B
C
D
M
N
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离C、D两加油站都越来越近?在哪一段路上距离加油站D越来越近,而离加油站C却越来越远?
(2)在公路
AB
的
AM
段距离
C、D
两加油站都越来越近,在
MN
段距离加油站
D
越来越近,而加油站
C
却越来越远.
A
B
C
D
M
N
学有所思,感悟收获
谈谈你的收获
能说出你这节课的收获和体验
让大家与你分享吗?
谢谢,请提出宝贵意见!
4.5
垂线
第2课时
垂线段与点到直线的距离
湘教版
七年级下册
1.理解垂线的画法;
2.
知道垂线段和点到直线的距离的概念,并会应用解决问题.
(重点、难点)
学习目标
思考:在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
情境引入
思考:在平面内,通过一点能不能画一条直线与已知直线垂直?如果可能,能够画几条?
把l
所在的纸片在P点折叠过来,使射线PB与PA重合,折痕是直线PM,如图,由于∠1=∠2,且∠1+∠2=______,所以∠1=∠2=_________,因此PM是过点P且垂直l的直线.
A
B
P
l
A
B
P
l
1
2
M
(1)如图,设P点在直线l上.
180°
90°
推进新课
(2)如图,设P点在直线
l
之外.
过点P
作直线l
'与
l
平行,通过P有一条直线MN⊥l
'
,从而MN⊥l
l
M
N
l'
P
因此,过一点P一定有一条直线与直线
l
垂直.
(1)
讨论:平面内过一点P能够有两条或两条以上的直线与直线
l
垂直吗?
在平面内,通过一点有一条且只有一条直线与已知直线垂直.
(2)
如果直线PC与PD都与l垂直,那么PC与PD的位置关系合怎样?
有且只能有一条
会重合
P
C
D
如图,设PO垂直于直线l,O为垂足,线段PO叫作P点到直线l
的垂线段.
P
B
l
O
A
C
通过P点的其他直线交
l
于A、B、
C…,线段PA,PB,PC都不是垂线段,称为斜线段.
(1)
如图,设P是直线l
外的一点,其细线一根,一端用图钉固定在P点,将细线拉直使它与l
垂直,在垂足O处作一标志,然后拉紧细线左右旋转至PA,PB等位置,比较PO,PA,PB的长度,你能从中猜出什么结论?
根据操作,我们不难猜想,所有这些线段中,垂线段PO最短.
p
O
这个猜想对吗?为什么?
(2)
用小纸片剪一个和三角形POB一样的三角形盖在三角形POB上,将纸片沿直线l翻折过来,得到三角形P'OB,
P
P'
B
O
l
或者简单地说成:
直线外一点与直线上各点连结的所有线段中,垂线段最短
这个猜想对吗?为什么?
如图,因为∠POB=∠P'OB=90?,所以POP'成一直线段,于是PO+P'O
在图中,垂线段PO的长度点到直线
l
的距离.
练习:如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
C
∟
垂线段最短
N
1.如图所示,某工厂要在河岸
l
上建一个水泵房引水到C处,问建在哪个位置上才最节省水管?为什么?
l
C
由C点向l作垂线,CP,垂足为P,所以建在P点上最节省水管.
P
垂线段最短
如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为D,AB=5,BC=12,AC=13.
求:(1)点A到BC的距离;
(2)点B到直线AC的距离.
A
D
C
B
解:(1)因为∠ABC=90°,
所以AB⊥BC,B为垂足.
所以线段AB即为点A到直线BC的垂线段.
因为AB=5,
所以点A到直线BC的距离为5.
(2)因为BD⊥AC,垂足为D,
所以线段BD的长度即为点B到直线AC的距离.
1.过点P
向线段AB
所在直线引垂线,正确的是(
)
A
B
C
D
C
当堂练习
2.如图,
AC⊥BC,
∠C=90°
,线段AC、BC、CD中最短
的是
(
)
A.
AC
B.
BC
C.
CD
D.
不能确定
D
A
B
C
C
3.
P
是直线
AB
外一点,过点
P
作
PO⊥AB
,垂足为
O
,若
C
为直线
AB
上任意一点,则线段
PC
与线段
PO
的大小关系是(
)
A.
PC
>
PO
B.
PC
<
PO
C.
PC
≥
PO
D.
PC
≤
PO
C
4.下列说法正确的是(
)
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
A
B
C
D
D
5.一辆汽车在直线形的公路AB上由A向B行驶,C、D
是分别位于公路AB两侧的加油站.
(1)设汽车行驶到公路AB上点M的位置时,距离加油站C最近;行驶到点N的位置时,距离加油站D最近,请在图中分别画出点M、N的位置;
A
B
C
D
M
N
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离C、D两加油站都越来越近?在哪一段路上距离加油站D越来越近,而离加油站C却越来越远?
(2)在公路
AB
的
AM
段距离
C、D
两加油站都越来越近,在
MN
段距离加油站
D
越来越近,而加油站
C
却越来越远.
A
B
C
D
M
N
学有所思,感悟收获
谈谈你的收获
能说出你这节课的收获和体验
让大家与你分享吗?
谢谢,请提出宝贵意见!
