北师大版八年级下册数学 6.3 三角形的中位线 同步测试卷含答案
文档属性
| 名称 | 北师大版八年级下册数学 6.3 三角形的中位线 同步测试卷含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 236.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 00:00:00 | ||
图片预览

文档简介
6.3
三角形的中位线
同步测试卷
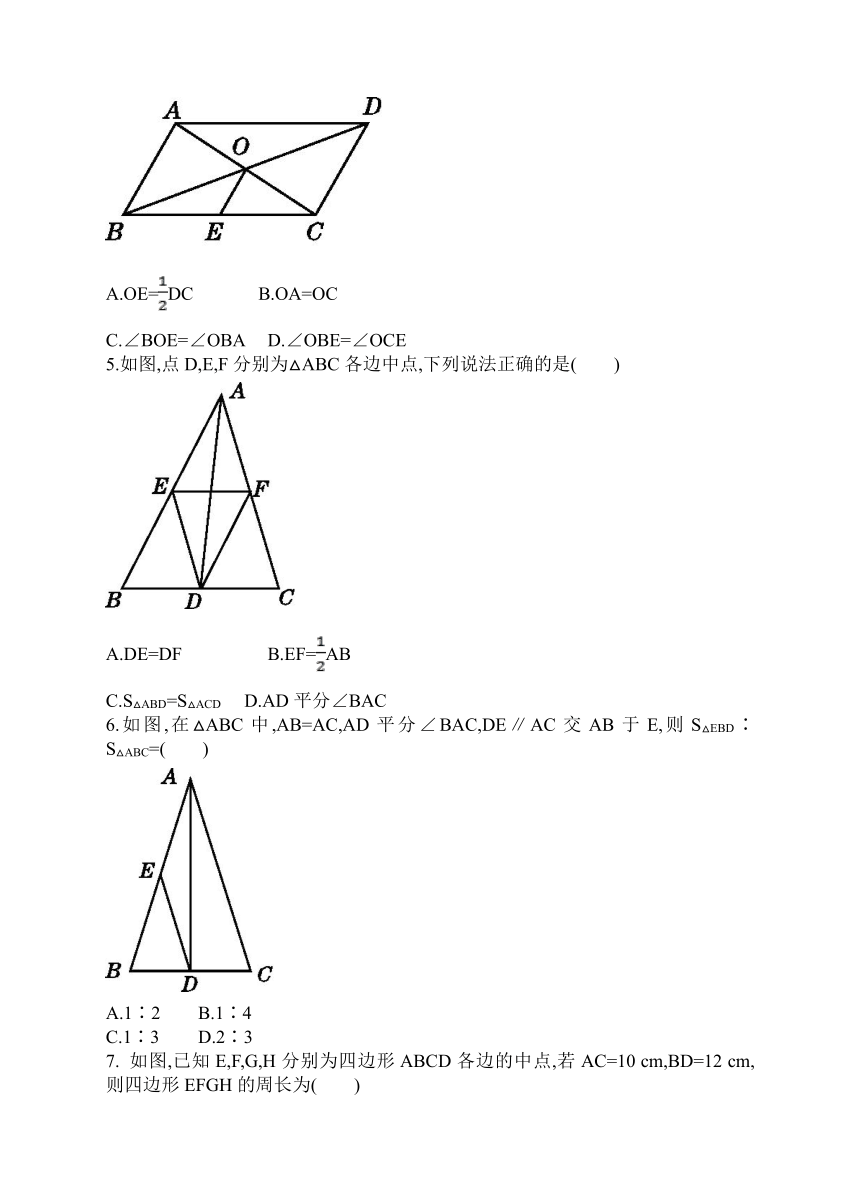
1.如图,在△ABC中,D,E分别是AB,AC的中点,若DE=10,则BC等于( )
A.12
B.16
C.20
D.24
2.如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为( )
A.6
B.5
C.4
D.3
3.如图,在△ABC中,点D,E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A.8
B.10
C.12
D.14
4.如图,已知四边形ABCD是平行四边形,对角线AC,BD交于点O,E是BC的中点,连接OE,以下说法错误的是( )
A.OE=DC
B.OA=OC
C.∠BOE=∠OBA
D.∠OBE=∠OCE
5.如图,点D,E,F分别为△ABC各边中点,下列说法正确的是( )
A.DE=DF
B.EF=AB
C.S△ABD=S△ACD
D.AD平分∠BAC
6.如图,在△ABC中,AB=AC,AD平分∠BAC,DE∥AC交AB于E,则S△EBD∶S△ABC=( )
A.1∶2
B.1∶4
C.1∶3
D.2∶3
7.
如图,已知E,F,G,H分别为四边形ABCD各边的中点,若AC=10
cm,BD=12
cm,则四边形EFGH的周长为( )
A.10
cm
B.11
cm
C.12
cm
D.22
cm
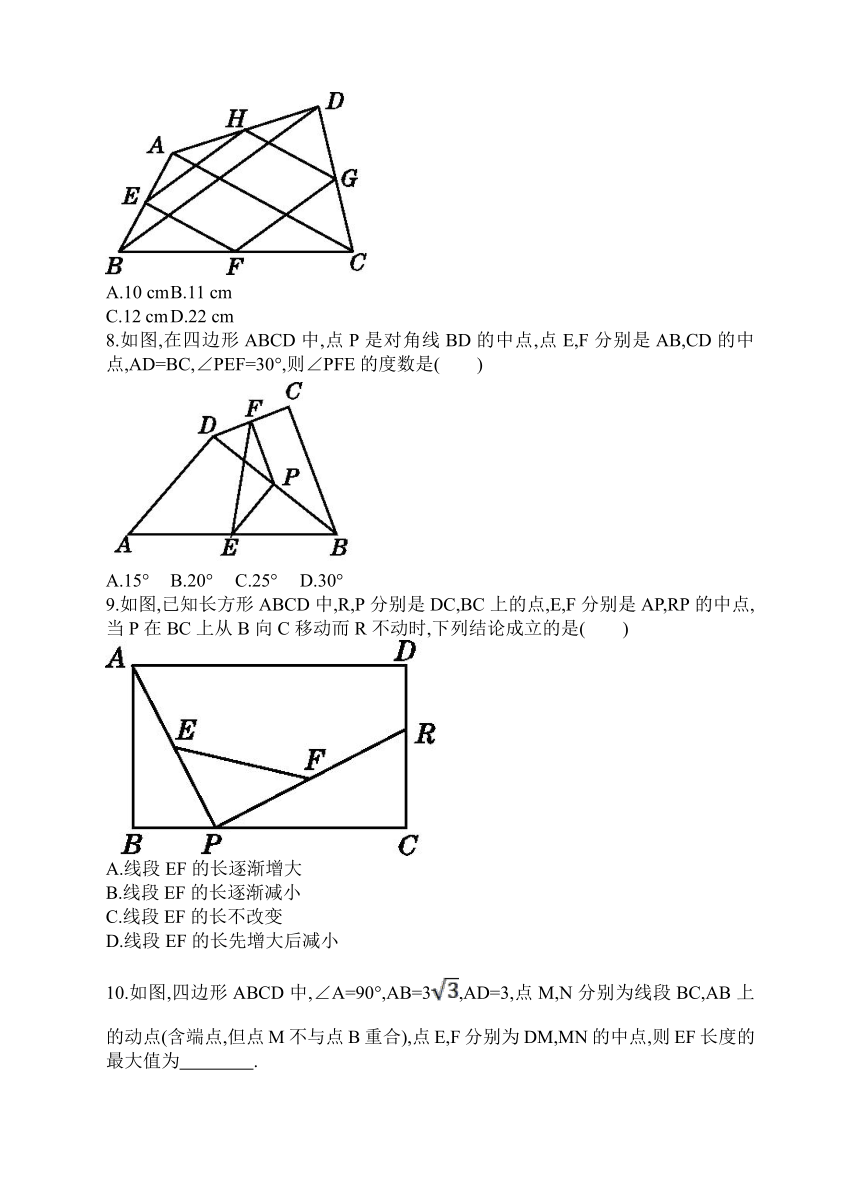
8.如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )
A.15°
B.20°
C.25°
D.30°
9.如图,已知长方形ABCD中,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当P在BC上从B向C移动而R不动时,下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不改变
D.线段EF的长先增大后减小
10.如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .?
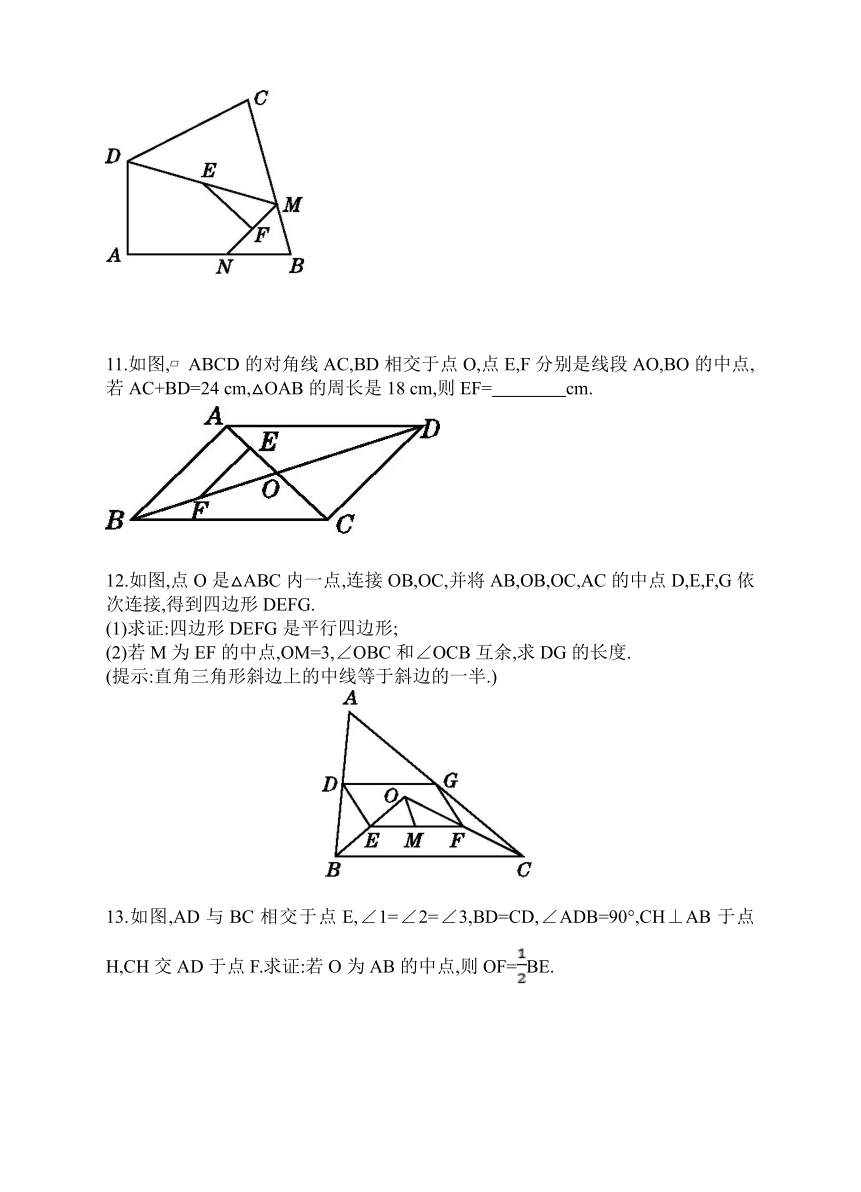
11.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24
cm,△OAB的周长是18
cm,则EF= cm.?
12.如图,点O是△ABC内一点,连接OB,OC,并将AB,OB,OC,AC的中点D,E,F,G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
(提示:直角三角形斜边上的中线等于斜边的一半.)
13.如图,AD与BC相交于点E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于点H,CH交AD于点F.求证:若O为AB的中点,则OF=BE.
14.如图,四边形ABCD中,AB=CD,G,H分别是BC,AD的中点,BA,CD的延长线分别交GH的延长线于点E,F.求证:∠AEH=∠F.
15.已知:如图,在?ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.
参考答案
1.【答案】C
解:因为D,E分别是AB,AC的中点,所以DE是△ABC的中位线,因此DE=BC,故BC=2DE=20.选C.
2.【答案】D
解:连接CE.∵在Rt△ACB中,∠ACB=90°,AC=8,AB=10,∴BC=6.
又∵DE垂直平分AC交AB于点E,
∴AE=CE.∴∠A=∠ACE.
又∵∠A+∠B=90°,∠ACE+∠BCE=90°,
∴∠B=∠BCE.∴CE=BE.
∴AE=BE.
∴DE是△ACB的中位线,
∴DE=BC=3.
故选D.
3.【答案】C
4.【答案】D
解:由平行四边形的性质和三角形中位线定理得出选项A,B,C正确;由OB≠OC,得出∠OBE≠∠OCE,故选项D错误.
5.
【答案】C
6.
【答案】B
7.
【答案】D
8.【答案】D
9.【答案】C
解:连接AR.因为E,F分别是AP,RP的中点,所以EF为△APR的中位线,所以EF=AR,为定值.所以线段EF的长不改变.故选C.
10.【答案】3
解:连接DN.∵E,F分别为DM,MN的中点,∴EF=DN,∴DN最大时,EF最大,∵N与B重合时DN最大,此时DN=DB==6,∴EF长度的最大值为3.
11.【答案】3
解:∵AC+BD=24
cm,∴OA+OB=12
cm,又∵△OAB的周长是18
cm,∴OA+OB+AB=18
cm,∴AB=6
cm.又∵点E,F分别是线段AO,BO的中点,∴EF=AB=3
cm.此题易错之处在于忽视运用整体思想求OA,OB的长度和,从而导致求不出中位线长.
12.分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,DG∥BC且DG=BC,从而得到DG=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)先判断出∠BOC=90°,再利用直角三角形斜边上的中线等于斜边的一半,求出EF即可.
(1)证明:∵D,G分别是AB,AC的中点,∴DG?BC.
∵E,F分别是OB,OC的中点,
∴EF?BC.
∴DG?EF.
∴四边形DEFG是平行四边形.
(2)解:∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°.
∴∠BOC=90°.
∵M为EF的中点,OM=3,
∴EF=2OM=6.
∵四边形DEFG是平行四边形,
∴DG=EF=6.
13.证明:∵BD=CD,∴∠1=∠BCD.
∵∠1=∠2,∴∠BCD=∠2.
∴CD∥AB,∴∠CDA=∠3.
又∵∠BCD=∠2=∠3,∴∠CDA=∠BCD,BE=AE,∴DE=CE.
又∵∠BED=∠AEC,
∴△BDE≌△ACE.
∴∠1=∠4,∠BDE=∠ACE=90°.
∴∠ACH=90°-∠BCH.
又∵CH⊥AB,∴∠2=90°-∠BCH,
∴∠ACH=∠2=∠1=∠4,
∴AF=CF.
又∵∠AEC=90°-∠4,∠ECF=90°-∠ACH,
∴∠AEC=∠ECF,
∴CF=EF,∴EF=AF.
又∵O为AB的中点,∴OF为△ABE的中位线,∴OF=BE.
方法总结:证明线段倍分关系的方法:由于三角形的中位线等于三角形第三边长的一半,因此当需要证明某一线段是另一线段的一半或两倍,且题中出现中点时,常考虑三角形中位线定理.
14.证明:如图,连接AC,取AC的中点M,连接HM,GM.
∵H是AD的中点,M是AC的中点,
∴HM∥CD,HM=CD.
∴∠MHG=∠F.
同理,GM∥AB,GM=AB.
∴∠MGH=∠AEH.
又∵AB=CD,∴GM=HM.
∴∠MGH=∠MHG.
∴∠AEH=∠F.
解:当几个中点不是一个三角形的各边中点时,可设法再取一个中点,使它与已知中点能构成三角形的中位线.此题中H,G分别是四边形ABCD两条对边的中点,这时需连接对角线,将四边形转化为两个三角形,再取对角线中点,与已知中点相连,就会产生三角形的中位线,问题便迎刃而解.
15.证明:如图,
取BE的中点H,连接FH,CH.
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线.
∴FH∥AB且FH=AB.
在?ABCD中,AB∥DC,AB=DC.
又∵点E是DC的中点,
∴EC=DC=AB,
∴FH=EC.
又∵AB∥DC,FH∥AB,∴FH∥EC,
∴四边形EFHC是平行四边形.
∴GF=GC.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
三角形的中位线
同步测试卷
1.如图,在△ABC中,D,E分别是AB,AC的中点,若DE=10,则BC等于( )
A.12
B.16
C.20
D.24
2.如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为( )
A.6
B.5
C.4
D.3
3.如图,在△ABC中,点D,E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A.8
B.10
C.12
D.14
4.如图,已知四边形ABCD是平行四边形,对角线AC,BD交于点O,E是BC的中点,连接OE,以下说法错误的是( )
A.OE=DC
B.OA=OC
C.∠BOE=∠OBA
D.∠OBE=∠OCE
5.如图,点D,E,F分别为△ABC各边中点,下列说法正确的是( )
A.DE=DF
B.EF=AB
C.S△ABD=S△ACD
D.AD平分∠BAC
6.如图,在△ABC中,AB=AC,AD平分∠BAC,DE∥AC交AB于E,则S△EBD∶S△ABC=( )
A.1∶2
B.1∶4
C.1∶3
D.2∶3
7.
如图,已知E,F,G,H分别为四边形ABCD各边的中点,若AC=10
cm,BD=12
cm,则四边形EFGH的周长为( )
A.10
cm
B.11
cm
C.12
cm
D.22
cm
8.如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )
A.15°
B.20°
C.25°
D.30°
9.如图,已知长方形ABCD中,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当P在BC上从B向C移动而R不动时,下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不改变
D.线段EF的长先增大后减小
10.如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .?
11.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24
cm,△OAB的周长是18
cm,则EF= cm.?
12.如图,点O是△ABC内一点,连接OB,OC,并将AB,OB,OC,AC的中点D,E,F,G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
(提示:直角三角形斜边上的中线等于斜边的一半.)
13.如图,AD与BC相交于点E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于点H,CH交AD于点F.求证:若O为AB的中点,则OF=BE.
14.如图,四边形ABCD中,AB=CD,G,H分别是BC,AD的中点,BA,CD的延长线分别交GH的延长线于点E,F.求证:∠AEH=∠F.
15.已知:如图,在?ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.
参考答案
1.【答案】C
解:因为D,E分别是AB,AC的中点,所以DE是△ABC的中位线,因此DE=BC,故BC=2DE=20.选C.
2.【答案】D
解:连接CE.∵在Rt△ACB中,∠ACB=90°,AC=8,AB=10,∴BC=6.
又∵DE垂直平分AC交AB于点E,
∴AE=CE.∴∠A=∠ACE.
又∵∠A+∠B=90°,∠ACE+∠BCE=90°,
∴∠B=∠BCE.∴CE=BE.
∴AE=BE.
∴DE是△ACB的中位线,
∴DE=BC=3.
故选D.
3.【答案】C
4.【答案】D
解:由平行四边形的性质和三角形中位线定理得出选项A,B,C正确;由OB≠OC,得出∠OBE≠∠OCE,故选项D错误.
5.
【答案】C
6.
【答案】B
7.
【答案】D
8.【答案】D
9.【答案】C
解:连接AR.因为E,F分别是AP,RP的中点,所以EF为△APR的中位线,所以EF=AR,为定值.所以线段EF的长不改变.故选C.
10.【答案】3
解:连接DN.∵E,F分别为DM,MN的中点,∴EF=DN,∴DN最大时,EF最大,∵N与B重合时DN最大,此时DN=DB==6,∴EF长度的最大值为3.
11.【答案】3
解:∵AC+BD=24
cm,∴OA+OB=12
cm,又∵△OAB的周长是18
cm,∴OA+OB+AB=18
cm,∴AB=6
cm.又∵点E,F分别是线段AO,BO的中点,∴EF=AB=3
cm.此题易错之处在于忽视运用整体思想求OA,OB的长度和,从而导致求不出中位线长.
12.分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,DG∥BC且DG=BC,从而得到DG=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)先判断出∠BOC=90°,再利用直角三角形斜边上的中线等于斜边的一半,求出EF即可.
(1)证明:∵D,G分别是AB,AC的中点,∴DG?BC.
∵E,F分别是OB,OC的中点,
∴EF?BC.
∴DG?EF.
∴四边形DEFG是平行四边形.
(2)解:∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°.
∴∠BOC=90°.
∵M为EF的中点,OM=3,
∴EF=2OM=6.
∵四边形DEFG是平行四边形,
∴DG=EF=6.
13.证明:∵BD=CD,∴∠1=∠BCD.
∵∠1=∠2,∴∠BCD=∠2.
∴CD∥AB,∴∠CDA=∠3.
又∵∠BCD=∠2=∠3,∴∠CDA=∠BCD,BE=AE,∴DE=CE.
又∵∠BED=∠AEC,
∴△BDE≌△ACE.
∴∠1=∠4,∠BDE=∠ACE=90°.
∴∠ACH=90°-∠BCH.
又∵CH⊥AB,∴∠2=90°-∠BCH,
∴∠ACH=∠2=∠1=∠4,
∴AF=CF.
又∵∠AEC=90°-∠4,∠ECF=90°-∠ACH,
∴∠AEC=∠ECF,
∴CF=EF,∴EF=AF.
又∵O为AB的中点,∴OF为△ABE的中位线,∴OF=BE.
方法总结:证明线段倍分关系的方法:由于三角形的中位线等于三角形第三边长的一半,因此当需要证明某一线段是另一线段的一半或两倍,且题中出现中点时,常考虑三角形中位线定理.
14.证明:如图,连接AC,取AC的中点M,连接HM,GM.
∵H是AD的中点,M是AC的中点,
∴HM∥CD,HM=CD.
∴∠MHG=∠F.
同理,GM∥AB,GM=AB.
∴∠MGH=∠AEH.
又∵AB=CD,∴GM=HM.
∴∠MGH=∠MHG.
∴∠AEH=∠F.
解:当几个中点不是一个三角形的各边中点时,可设法再取一个中点,使它与已知中点能构成三角形的中位线.此题中H,G分别是四边形ABCD两条对边的中点,这时需连接对角线,将四边形转化为两个三角形,再取对角线中点,与已知中点相连,就会产生三角形的中位线,问题便迎刃而解.
15.证明:如图,
取BE的中点H,连接FH,CH.
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线.
∴FH∥AB且FH=AB.
在?ABCD中,AB∥DC,AB=DC.
又∵点E是DC的中点,
∴EC=DC=AB,
∴FH=EC.
又∵AB∥DC,FH∥AB,∴FH∥EC,
∴四边形EFHC是平行四边形.
∴GF=GC.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
