北师大版数学七年级下册 4.3.1“边边边”判定 教案
文档属性
| 名称 | 北师大版数学七年级下册 4.3.1“边边边”判定 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 00:00:00 | ||
图片预览


文档简介
4.3.1
探索三角形全等的条件(1)边边边公理教学设计
●教学目标
(一)知识与技能
1.掌握三角形全等的“边边边”条件,了解三角形的稳定性.
2.
在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.
(二)过程与方法
经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
(三)情感与价值观要求
1.使学生在自主探索三角形全等的过程中,经历画图、观察、比较、推理、交流等环节,从而获得正确的学习方式和良好的情感体验.
2.让学生体验数学来源于生活,服务于生活的辩证思想.
●教学重点:
三角形全等的条件.
●教学难点:
三角形全等的条件.
●教学方法:
讨论、引导教学法.
●教学过程
一.巧设现实情景,引入新课
[师]前面我们研究了全等三角形.现在我们来回忆一下:(出示投影片)
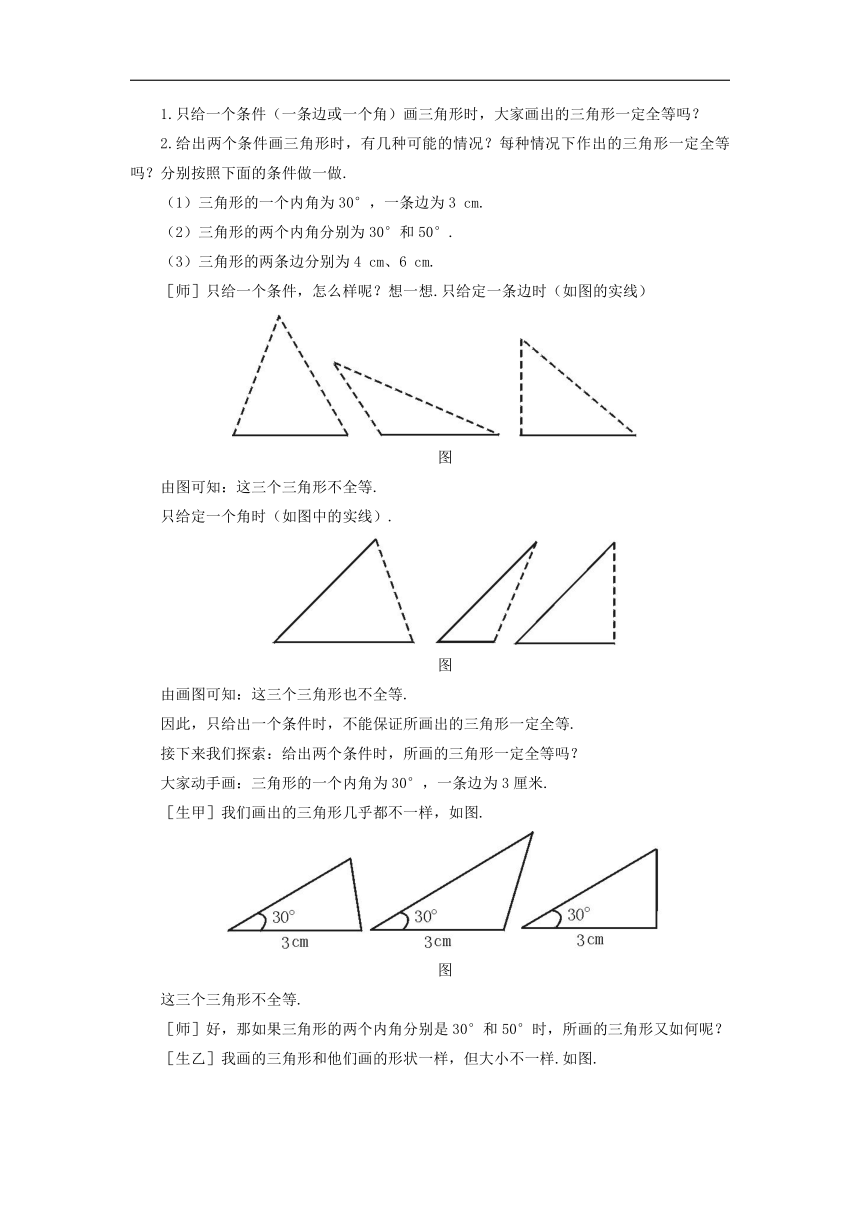
如图
图
已知:△ABC≌△DEF,找出其中相等的边与角.
[生]图中相等的边是:AB=DE、BC=EF、AC=DF.
相等的角是:∠A=∠D、∠B=∠E、∠C=∠F.
[师]很好.我这里有一个三角形纸片,你能画一个三角形与它全等吗?如何画?
[师]你们要画一个三角形与我的三角形全等。需要几个与边或角的大小有关的条件?只知道一个条件行吗?两个条件呢?三个条件呢?我们这节课就来探索三角形全等的条件.
二.讲授新课
[师]下面我们来做一做(出示投影片)
1.只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
2.给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做.
(1)三角形的一个内角为30°,一条边为3
cm.
(2)三角形的两个内角分别为30°和50°.
(3)三角形的两条边分别为4
cm、6
cm.
[师]只给一个条件,怎么样呢?想一想.只给定一条边时(如图的实线)
图
由图可知:这三个三角形不全等.
只给定一个角时(如图中的实线).
图
由画图可知:这三个三角形也不全等.
因此,只给出一个条件时,不能保证所画出的三角形一定全等.
接下来我们探索:给出两个条件时,所画的三角形一定全等吗?
大家动手画:三角形的一个内角为30°,一条边为3厘米.
[生甲]我们画出的三角形几乎都不一样,如图.
图
这三个三角形不全等.
[师]好,那如果三角形的两个内角分别是30°和50°时,所画的三角形又如何呢?
[生乙]我画的三角形和他们画的形状一样,但大小不一样.如图.
图
这两个三角形不能重合,即不全等.
[师]很好.如果给定三角形的两边分别为4
cm、6
cm,那么所画出的三角形全等吗?
[生丙]也不全等.如图5-103.
图
[师]很好,我们通过画图、观察、比较知道,只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等.
那给出三个条件时,又怎样呢?大家来议一议(出示投影片).
如果给出三个条件画三角形,你能说出有哪几种可能的情况?
[生丁]有四种可能.即:三条边,三个角,两边一角和两角一边.
[师]对,下面我们来逐一探索(出示投影片)
做一做:
已知一个三角形的三条边分别为4
cm、5
cm和7
cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
那给出三角形的三条边又如何呢?
[生乙]已知一个三角形的三条边分别是4
cm,5
cm和7
cm,我能画出这个三角形.与同伴们进行比较可知:这样的所有三角形都是全等的.
[生丙]我画的三角形也和别人画的全等.由此可知:已知三角形的三边,则画出的所有三角形都全等.
[师]好,由此我们知道:已知三角形的三条边画三角形,则画出的所有三角形全等(电脑演示重合过程).这样就得到了三角形全等的条件:
三边对应相等的两个三角形全等.
简写为:“边边边”或“SSS”
如图.
图
△ABC≌△DEF.
下面我们来做一个实验(出示投影片)
取三根长度适当的木条,用钉子钉成一个三角形的框架,你所得到的框架的形状固定吗?用四根木条钉成的框架的形状固定吗?
[师]做实验时,可用细纸条代替木条.实验后分组讨论.
[生]用三根木条钉成的三角形框架是固定的,用四根木条钉成的框架,它的形状是可以改变的.
[师]很好,看屏幕(演示图).
图
图(1)是用三根木条钉成的三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性.三角形的稳定性在生产和生活中是很有用的.如:房屋的人字梁具有三角形的结构,它就坚固和稳定.
图(2)的形状是可以改变的,它不具有稳定性.
大家想一想,如何才能使图(2)的框架不能活动?
[生]在相对的顶点上钉一根木条,使它变为两个三角形框架即可.
[师]对,在生活中经常会看到采用三角形的结构去建筑.就是用到了它的稳定性.同学们能举出一些生活中应用三角形的稳定性的例子吗?
[生]能.如:大桥钢架、索道支架、输电线支架等等.
[师]很好,下面我们来做一练习以熟悉掌握本节内容.
三.课堂练习
例题1、如图甲,当
AB=CD,BC=DA时,图中的△ABC与△CDA是否全等?并说明理由。
变式:如图乙,当
AB=CD,BC=DA时,你能说明AB与CD、AD与BC的位置关系吗?为什么?
图甲
图乙
2.已知:如图1,AC、BD相交于点O,且AB=DC,AC=DB,那么∠A=∠D吗?为什么?
图1
四.课时小结
本节课我们重点探索了三角形全等的条件,还了解了三角形的稳定性.
三角形全等的条件:
三边对应相等的两个三角形全等.
如图.
图
△ABC≌△DEF.
五、课本习题3.6
3
●板书设计
4.3.1
探索三角形全等的条件
一、三角形全等的条件:
三边对应相等的两个三角形全等.“SSS”
二、三角形的稳定性.
三、课堂练习
四、课时小结
五、课后作业
探索三角形全等的条件(1)边边边公理教学设计
●教学目标
(一)知识与技能
1.掌握三角形全等的“边边边”条件,了解三角形的稳定性.
2.
在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.
(二)过程与方法
经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
(三)情感与价值观要求
1.使学生在自主探索三角形全等的过程中,经历画图、观察、比较、推理、交流等环节,从而获得正确的学习方式和良好的情感体验.
2.让学生体验数学来源于生活,服务于生活的辩证思想.
●教学重点:
三角形全等的条件.
●教学难点:
三角形全等的条件.
●教学方法:
讨论、引导教学法.
●教学过程
一.巧设现实情景,引入新课
[师]前面我们研究了全等三角形.现在我们来回忆一下:(出示投影片)
如图
图
已知:△ABC≌△DEF,找出其中相等的边与角.
[生]图中相等的边是:AB=DE、BC=EF、AC=DF.
相等的角是:∠A=∠D、∠B=∠E、∠C=∠F.
[师]很好.我这里有一个三角形纸片,你能画一个三角形与它全等吗?如何画?
[师]你们要画一个三角形与我的三角形全等。需要几个与边或角的大小有关的条件?只知道一个条件行吗?两个条件呢?三个条件呢?我们这节课就来探索三角形全等的条件.
二.讲授新课
[师]下面我们来做一做(出示投影片)
1.只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
2.给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做.
(1)三角形的一个内角为30°,一条边为3
cm.
(2)三角形的两个内角分别为30°和50°.
(3)三角形的两条边分别为4
cm、6
cm.
[师]只给一个条件,怎么样呢?想一想.只给定一条边时(如图的实线)
图
由图可知:这三个三角形不全等.
只给定一个角时(如图中的实线).
图
由画图可知:这三个三角形也不全等.
因此,只给出一个条件时,不能保证所画出的三角形一定全等.
接下来我们探索:给出两个条件时,所画的三角形一定全等吗?
大家动手画:三角形的一个内角为30°,一条边为3厘米.
[生甲]我们画出的三角形几乎都不一样,如图.
图
这三个三角形不全等.
[师]好,那如果三角形的两个内角分别是30°和50°时,所画的三角形又如何呢?
[生乙]我画的三角形和他们画的形状一样,但大小不一样.如图.
图
这两个三角形不能重合,即不全等.
[师]很好.如果给定三角形的两边分别为4
cm、6
cm,那么所画出的三角形全等吗?
[生丙]也不全等.如图5-103.
图
[师]很好,我们通过画图、观察、比较知道,只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等.
那给出三个条件时,又怎样呢?大家来议一议(出示投影片).
如果给出三个条件画三角形,你能说出有哪几种可能的情况?
[生丁]有四种可能.即:三条边,三个角,两边一角和两角一边.
[师]对,下面我们来逐一探索(出示投影片)
做一做:
已知一个三角形的三条边分别为4
cm、5
cm和7
cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
那给出三角形的三条边又如何呢?
[生乙]已知一个三角形的三条边分别是4
cm,5
cm和7
cm,我能画出这个三角形.与同伴们进行比较可知:这样的所有三角形都是全等的.
[生丙]我画的三角形也和别人画的全等.由此可知:已知三角形的三边,则画出的所有三角形都全等.
[师]好,由此我们知道:已知三角形的三条边画三角形,则画出的所有三角形全等(电脑演示重合过程).这样就得到了三角形全等的条件:
三边对应相等的两个三角形全等.
简写为:“边边边”或“SSS”
如图.
图
△ABC≌△DEF.
下面我们来做一个实验(出示投影片)
取三根长度适当的木条,用钉子钉成一个三角形的框架,你所得到的框架的形状固定吗?用四根木条钉成的框架的形状固定吗?
[师]做实验时,可用细纸条代替木条.实验后分组讨论.
[生]用三根木条钉成的三角形框架是固定的,用四根木条钉成的框架,它的形状是可以改变的.
[师]很好,看屏幕(演示图).
图
图(1)是用三根木条钉成的三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性.三角形的稳定性在生产和生活中是很有用的.如:房屋的人字梁具有三角形的结构,它就坚固和稳定.
图(2)的形状是可以改变的,它不具有稳定性.
大家想一想,如何才能使图(2)的框架不能活动?
[生]在相对的顶点上钉一根木条,使它变为两个三角形框架即可.
[师]对,在生活中经常会看到采用三角形的结构去建筑.就是用到了它的稳定性.同学们能举出一些生活中应用三角形的稳定性的例子吗?
[生]能.如:大桥钢架、索道支架、输电线支架等等.
[师]很好,下面我们来做一练习以熟悉掌握本节内容.
三.课堂练习
例题1、如图甲,当
AB=CD,BC=DA时,图中的△ABC与△CDA是否全等?并说明理由。
变式:如图乙,当
AB=CD,BC=DA时,你能说明AB与CD、AD与BC的位置关系吗?为什么?
图甲
图乙
2.已知:如图1,AC、BD相交于点O,且AB=DC,AC=DB,那么∠A=∠D吗?为什么?
图1
四.课时小结
本节课我们重点探索了三角形全等的条件,还了解了三角形的稳定性.
三角形全等的条件:
三边对应相等的两个三角形全等.
如图.
图
△ABC≌△DEF.
五、课本习题3.6
3
●板书设计
4.3.1
探索三角形全等的条件
一、三角形全等的条件:
三边对应相等的两个三角形全等.“SSS”
二、三角形的稳定性.
三、课堂练习
四、课时小结
五、课后作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
