华东师大版数学八年级下册:19.2.2菱形的判定课件(19张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册:19.2.2菱形的判定课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 13:55:26 | ||
图片预览



文档简介
(共19张PPT)
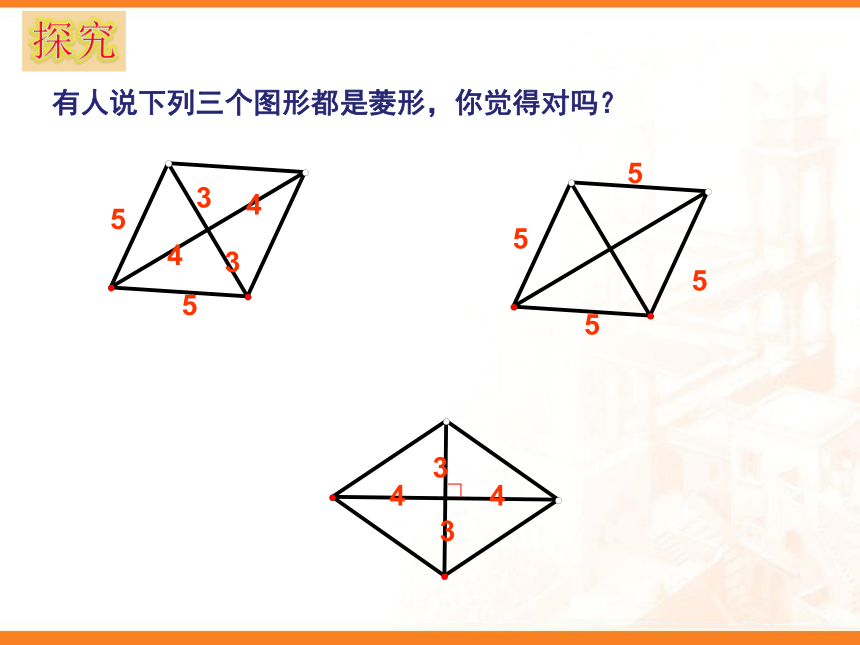
探究菱形的判定
边
边
角
对角线
对角线
菱形的性质
每条对角线平分一组对角
定义:有一组邻边相等的平行四边形是菱形
学习目标
1、掌握菱形的判定定理及证明方法。
2、学会运用菱形的判定解决一些问题;进一步发展合情推理能力
3、感受探索菱形判定的过程,培养主动探索、研究的习惯。
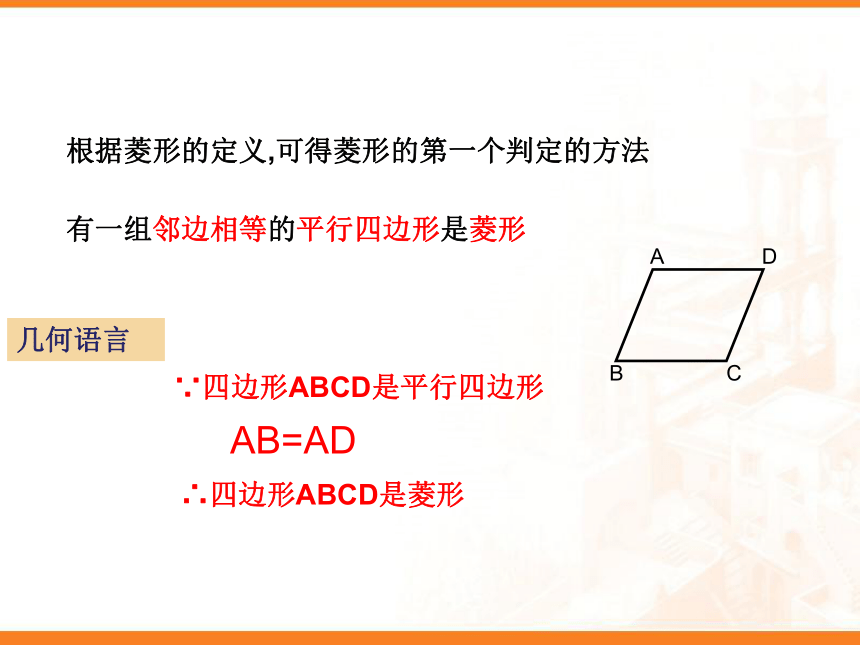
有人说下列三个图形都是菱形,你觉得对吗?
根据菱形的定义,可得菱形的第一个判定的方法
AB=AD
∵四边形ABCD是平行四边形
∴四边形ABCD是菱形
几何语言
有一组邻边相等的平行四边形是菱形
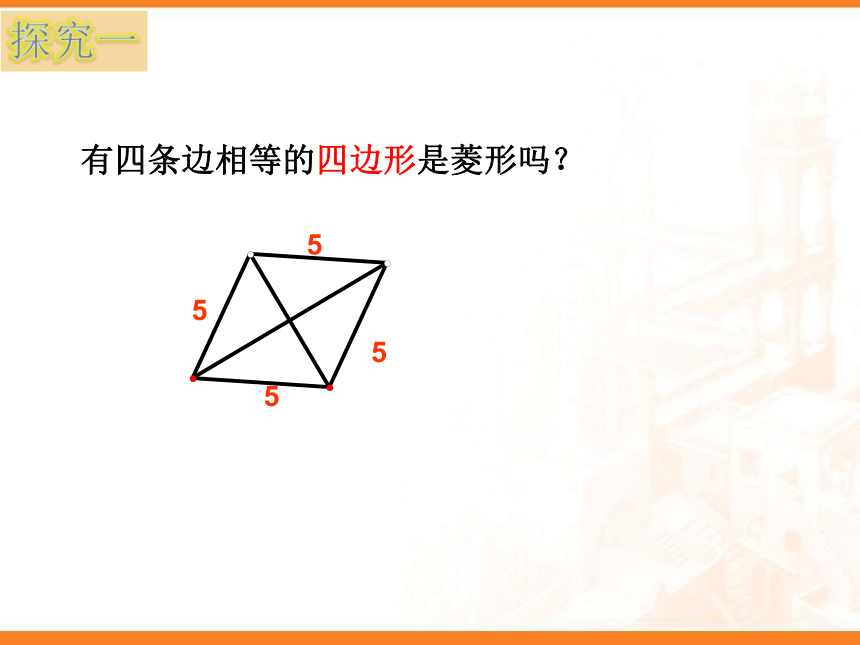
有四条边相等的四边形是菱形吗?
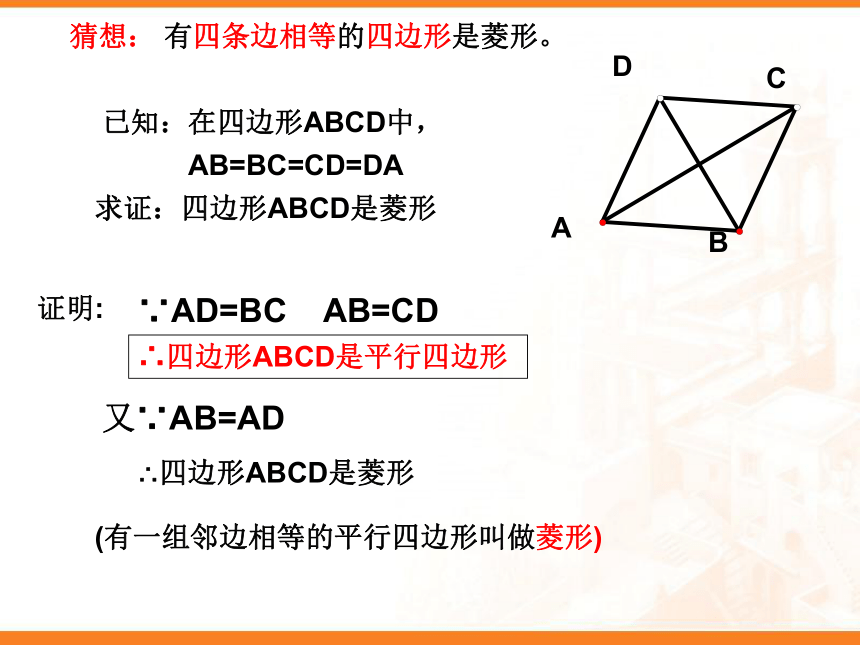
猜想:
有四条边相等的四边形是菱形。
∴四边形ABCD是平行四边形
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC
AB=CD
又∵AB=AD
A
B
C
D
有二条边相等的四边形是菱形吗?
有三条边相等的四边形是菱形吗?
猜想:对角线互相垂直的平行四边形是菱形.
已知:在平行四边形ABCD中,AC⊥BD
.
求证:平行四边形ABCD是菱形.
证明:
∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BA=BC,
∴
平行四边形ABCD是菱形.(有一组邻边相等的平行四边形是菱形)
定理:对角线互相垂直的平行四边形是菱形.
有人说下列三个图形都是菱形,对吗?
有一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四条边都相等的四边形是菱形
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
∵
四边形ABCD是平行四边形
AC⊥BD
∴
四边形ABCD是菱形
∵
四边形ABCD是平行四边形
AB=AD
∴
四边形ABCD是菱形
四边都相等的四边形是菱形
∵AB=BC=CD=DA
∴
四边形ABCD是菱形
1.如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是(
)
A.AC⊥BD
B.AB=AC
C.∠ABC=90°
D.AC=BD
2.如图,在?ABCD中,AC平分∠DAB,AB=2,则?ABCD的周长为(
)
A.4
B.6
C.8
D.12
?3.如图,小明在作线段AB的垂直平分线时,是这样操作的:
分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,
相交于点C,D,则直线CD即为所求,连接AC,BC,BD,AD,
根据他的作图方法可知,四边形ADBC一定是
形.
A
C
菱
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
4、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若AC⊥BD,则□ABCD是_____形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
菱
矩
菱
菱
学
以
致
用
如图,□ABCD对角线AC的垂直平分线与边AD、BC分别交于E,F.
求证:四边形AFCE是菱形;
1、本节课我们学习了什么?
2、在学习知识的过程中,你体会或者应用到
了哪些思想方法?
有一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四条边都相等的四边形是菱形
—寄语
严格性之于数学家,犹如道德之于人.
条理清晰,因果相应,言必有据.
是初学证明者谨记和遵循的原则.
谢谢
开动脑筋找方案
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
有人说下列三个图形都是菱形,你觉得对吗?
探究菱形的判定
边
边
角
对角线
对角线
菱形的性质
每条对角线平分一组对角
定义:有一组邻边相等的平行四边形是菱形
学习目标
1、掌握菱形的判定定理及证明方法。
2、学会运用菱形的判定解决一些问题;进一步发展合情推理能力
3、感受探索菱形判定的过程,培养主动探索、研究的习惯。
有人说下列三个图形都是菱形,你觉得对吗?
根据菱形的定义,可得菱形的第一个判定的方法
AB=AD
∵四边形ABCD是平行四边形
∴四边形ABCD是菱形
几何语言
有一组邻边相等的平行四边形是菱形
有四条边相等的四边形是菱形吗?
猜想:
有四条边相等的四边形是菱形。
∴四边形ABCD是平行四边形
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC
AB=CD
又∵AB=AD
A
B
C
D
有二条边相等的四边形是菱形吗?
有三条边相等的四边形是菱形吗?
猜想:对角线互相垂直的平行四边形是菱形.
已知:在平行四边形ABCD中,AC⊥BD
.
求证:平行四边形ABCD是菱形.
证明:
∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BA=BC,
∴
平行四边形ABCD是菱形.(有一组邻边相等的平行四边形是菱形)
定理:对角线互相垂直的平行四边形是菱形.
有人说下列三个图形都是菱形,对吗?
有一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四条边都相等的四边形是菱形
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
∵
四边形ABCD是平行四边形
AC⊥BD
∴
四边形ABCD是菱形
∵
四边形ABCD是平行四边形
AB=AD
∴
四边形ABCD是菱形
四边都相等的四边形是菱形
∵AB=BC=CD=DA
∴
四边形ABCD是菱形
1.如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是(
)
A.AC⊥BD
B.AB=AC
C.∠ABC=90°
D.AC=BD
2.如图,在?ABCD中,AC平分∠DAB,AB=2,则?ABCD的周长为(
)
A.4
B.6
C.8
D.12
?3.如图,小明在作线段AB的垂直平分线时,是这样操作的:
分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,
相交于点C,D,则直线CD即为所求,连接AC,BC,BD,AD,
根据他的作图方法可知,四边形ADBC一定是
形.
A
C
菱
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
4、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若AC⊥BD,则□ABCD是_____形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
菱
矩
菱
菱
学
以
致
用
如图,□ABCD对角线AC的垂直平分线与边AD、BC分别交于E,F.
求证:四边形AFCE是菱形;
1、本节课我们学习了什么?
2、在学习知识的过程中,你体会或者应用到
了哪些思想方法?
有一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四条边都相等的四边形是菱形
—寄语
严格性之于数学家,犹如道德之于人.
条理清晰,因果相应,言必有据.
是初学证明者谨记和遵循的原则.
谢谢
开动脑筋找方案
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
有人说下列三个图形都是菱形,你觉得对吗?
