青岛版七年级数学下册13.3.1《圆》课件(共20张PPT)
文档属性
| 名称 | 青岛版七年级数学下册13.3.1《圆》课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
导入新课
这些车轮都是什么形状呢
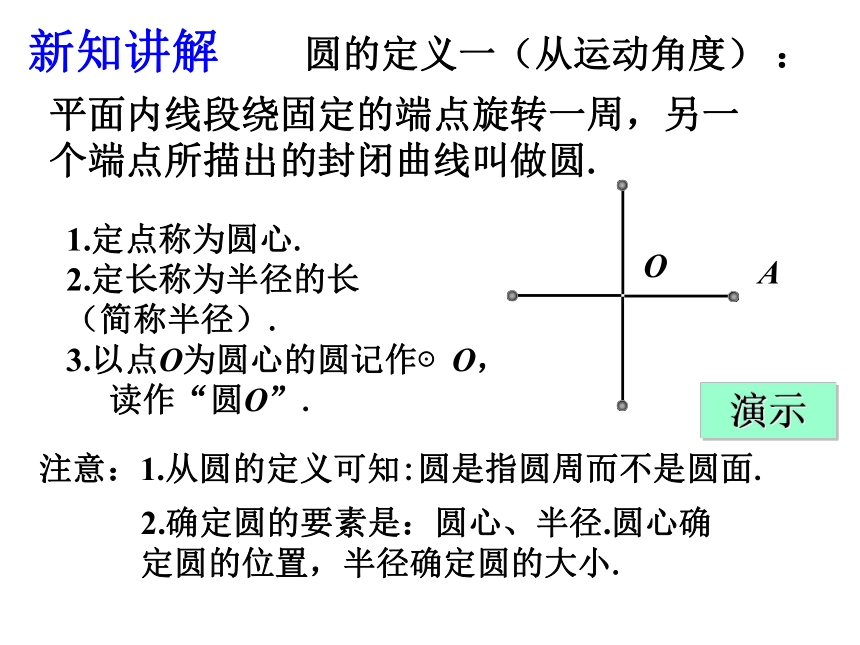
平面内线段绕固定的端点旋转一周,另一个端点所描出的封闭曲线叫做圆.
注意:1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是:圆心、半径.圆心确定圆的位置,半径确定圆的大小.
1.定点称为圆心.
2.定长称为半径的长
(简称半径).
3.以点O为圆心的圆记作⊙O,读作“圆O”.
圆的定义一(从运动角度)
:
演示
O
A
新知讲解
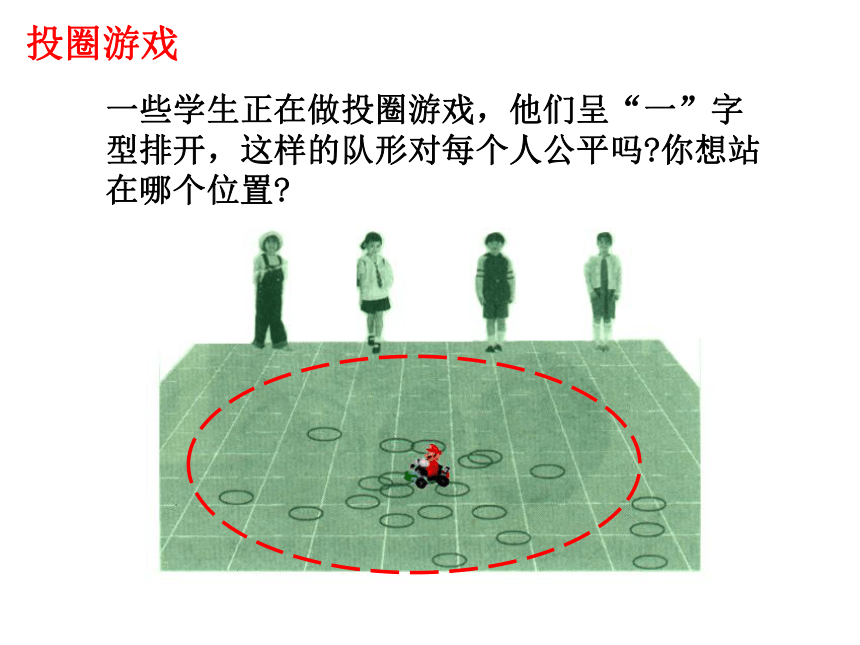
投圈游戏
一些学生正在做投圈游戏,他们呈“一”字型排开,这样的队形对每个人公平吗?你想站在哪个位置?
如图所示,
⊙O是一个半径为r的圆.在圆内、圆外、圆
上分别取一点,点到圆心的距离为d,请用r与d的大小
来刻画它们的位置特征.
点与圆位置关系有三种:
点在圆外、点在圆上、点在圆内
点在圆外,即d
>
r;
点在圆上,即d
=
r;
点在圆外,即d
<
r.
.O
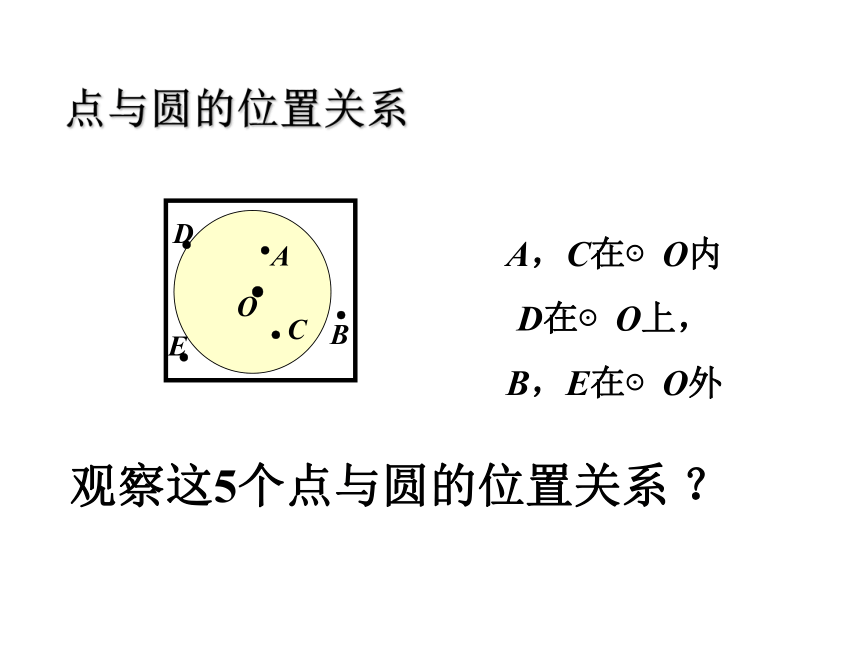
点与圆的位置关系
观察这5个点与圆的位置关系
?
A,C在⊙O内
D在⊙O上,
B,E在⊙O外
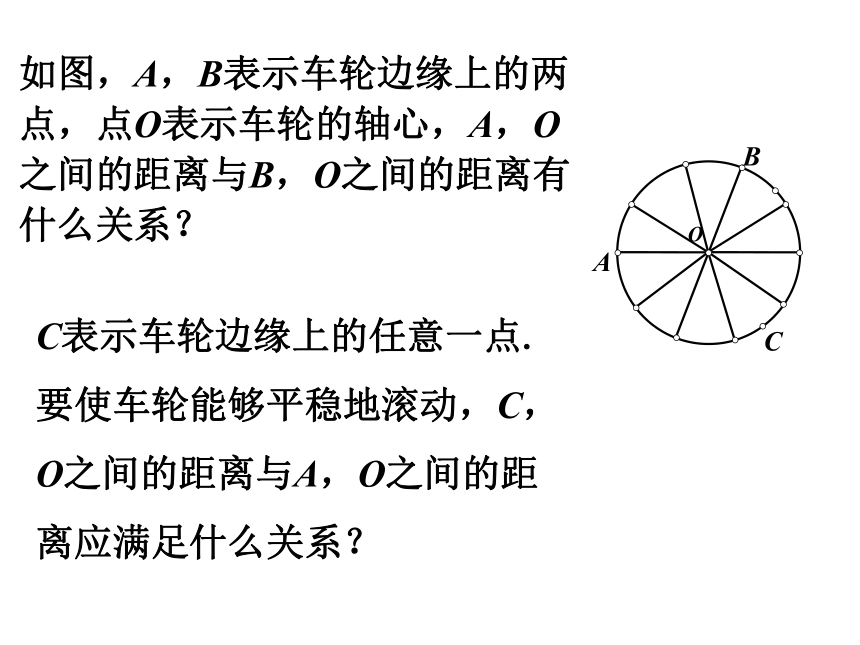
如图,A,B表示车轮边缘上的两点,点O表示车轮的轴心,A,O之间的距离与B,O之间的距离有什么关系?
C表示车轮边缘上的任意一点.
要使车轮能够平稳地滚动,C,
O之间的距离与A,O之间的距
离应满足什么关系?
圆是到定点的距离等于定长的点的集合.
圆的内部可以看作是到圆心的距离小于半径的点的集合.
圆的外部可以看作是到圆心的距离大于半径的点的集合.
圆的定义二(从集合角度)
:
车轮边缘上任意两点到轴心的距离都相等,
任意一点到轴心的距离是一个定值.
认识弧、弦、直径这些与圆有关的概念
1.弦:
2.弧:
如图,
(劣弧)、
(优弧)
如图,
弦AB,弦CD
如图,直径CD
圆上任意两点间的部分叫做圆弧,简称弧.
连接圆上任意两点的线段叫做弦.
直径:经过圆心的弦叫做直径.
半圆:圆的任意一条直径的两个端点分圆
成两条弧,每条弧叫做半圆.
认识与圆有关的概念
4.同心圆:圆心相同,半径不同的圆叫做同心圆.
3.等圆:能够重合的两个圆叫做等圆.
同心圆
等圆
确定一个圆的要素
圆心与半径
两张图片中的圆各有什么特征
圆心相同,半径不同
半径相同,圆心不同
例1
两个同心圆之间的部分叫做圆环.如果圆环中大圆的半径为r,小圆的半径为
,求圆环的面积.
解:圆环的面积等于大圆面积与小圆面积的差,所以圆环的面积为
例2
(1)用长度分别为1米和2米的两根绳子围成两个同心圆,这两个圆半径之差是多少?
(2)把地球的赤道近似地看做一个圆.如果环绕地球赤道有一个圆,它的周长比赤道的周长多1米,这两个同心圆半径之差是多少?想想看,两圆之间能伸进你的拳头吗?
解:(1)1米长的绳子围成的圆的半径为
米,2米长的绳子围成的圆的半径为
米.所以,两个同心圆的半径之差为
(米)
(2)设地球的半径为r,因为赤道与环绕赤道的圆是两个同心圆,所以这两个圆半径之差为
(米)
一个成年人的拳头高约8厘米,所以两圆之间能伸进一个人的拳头。
1、判断正误:
(1)
弦是直径(
)
(2)半圆是弧(
)
(3)
过圆心的线段是直径
(
)
(4)过圆心的直线是直径
(
)
(5)
半圆是最长的弧(
)
(6)
直径是最长的弦(
)
(7)
圆心相同,半径不等的两个圆是同心圆
(
)
(8)
半径相等的两个圆是等圆
(
)
错
对
对
错
错
对
错
习题巩固
对
2、已知⊙O的面积为16π,判断点P与⊙O的位置关系.
(1)若PO=4.5,则点P在
;
(2)若PO
=
3,则点P在
;
(3)若PO
=
(
),则点P在圆上.
⊙O外
⊙O内
4
3、已知AB
=3cm,作图说明满足下列要求的图形:
(4)
到点A和点B的距离都小于2cm的所有点组成的图形.
(3)
到点A和B的距离都等于2cm的所有点组成的图形.
(1)
到点A的距离等于2cm的所有点组成的图形.
(2)
到点B的距离等于2cm的所有点组成的图形.
B
A
定义一:
在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆.
固定的端点O叫做圆心,线段OA叫做半径.
1、从运动和集合的观点理解圆的定义:
定义二:圆是到定点的距离等于定长的点的集合.
3、证明几个点在同一个圆上的方法.
要证明几个点在同一个圆上,只要证明这几个点与一个定点的距离相等.
2、点与圆的位置关系:
课堂小结
导入新课
这些车轮都是什么形状呢
平面内线段绕固定的端点旋转一周,另一个端点所描出的封闭曲线叫做圆.
注意:1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是:圆心、半径.圆心确定圆的位置,半径确定圆的大小.
1.定点称为圆心.
2.定长称为半径的长
(简称半径).
3.以点O为圆心的圆记作⊙O,读作“圆O”.
圆的定义一(从运动角度)
:
演示
O
A
新知讲解
投圈游戏
一些学生正在做投圈游戏,他们呈“一”字型排开,这样的队形对每个人公平吗?你想站在哪个位置?
如图所示,
⊙O是一个半径为r的圆.在圆内、圆外、圆
上分别取一点,点到圆心的距离为d,请用r与d的大小
来刻画它们的位置特征.
点与圆位置关系有三种:
点在圆外、点在圆上、点在圆内
点在圆外,即d
>
r;
点在圆上,即d
=
r;
点在圆外,即d
<
r.
.O
点与圆的位置关系
观察这5个点与圆的位置关系
?
A,C在⊙O内
D在⊙O上,
B,E在⊙O外
如图,A,B表示车轮边缘上的两点,点O表示车轮的轴心,A,O之间的距离与B,O之间的距离有什么关系?
C表示车轮边缘上的任意一点.
要使车轮能够平稳地滚动,C,
O之间的距离与A,O之间的距
离应满足什么关系?
圆是到定点的距离等于定长的点的集合.
圆的内部可以看作是到圆心的距离小于半径的点的集合.
圆的外部可以看作是到圆心的距离大于半径的点的集合.
圆的定义二(从集合角度)
:
车轮边缘上任意两点到轴心的距离都相等,
任意一点到轴心的距离是一个定值.
认识弧、弦、直径这些与圆有关的概念
1.弦:
2.弧:
如图,
(劣弧)、
(优弧)
如图,
弦AB,弦CD
如图,直径CD
圆上任意两点间的部分叫做圆弧,简称弧.
连接圆上任意两点的线段叫做弦.
直径:经过圆心的弦叫做直径.
半圆:圆的任意一条直径的两个端点分圆
成两条弧,每条弧叫做半圆.
认识与圆有关的概念
4.同心圆:圆心相同,半径不同的圆叫做同心圆.
3.等圆:能够重合的两个圆叫做等圆.
同心圆
等圆
确定一个圆的要素
圆心与半径
两张图片中的圆各有什么特征
圆心相同,半径不同
半径相同,圆心不同
例1
两个同心圆之间的部分叫做圆环.如果圆环中大圆的半径为r,小圆的半径为
,求圆环的面积.
解:圆环的面积等于大圆面积与小圆面积的差,所以圆环的面积为
例2
(1)用长度分别为1米和2米的两根绳子围成两个同心圆,这两个圆半径之差是多少?
(2)把地球的赤道近似地看做一个圆.如果环绕地球赤道有一个圆,它的周长比赤道的周长多1米,这两个同心圆半径之差是多少?想想看,两圆之间能伸进你的拳头吗?
解:(1)1米长的绳子围成的圆的半径为
米,2米长的绳子围成的圆的半径为
米.所以,两个同心圆的半径之差为
(米)
(2)设地球的半径为r,因为赤道与环绕赤道的圆是两个同心圆,所以这两个圆半径之差为
(米)
一个成年人的拳头高约8厘米,所以两圆之间能伸进一个人的拳头。
1、判断正误:
(1)
弦是直径(
)
(2)半圆是弧(
)
(3)
过圆心的线段是直径
(
)
(4)过圆心的直线是直径
(
)
(5)
半圆是最长的弧(
)
(6)
直径是最长的弦(
)
(7)
圆心相同,半径不等的两个圆是同心圆
(
)
(8)
半径相等的两个圆是等圆
(
)
错
对
对
错
错
对
错
习题巩固
对
2、已知⊙O的面积为16π,判断点P与⊙O的位置关系.
(1)若PO=4.5,则点P在
;
(2)若PO
=
3,则点P在
;
(3)若PO
=
(
),则点P在圆上.
⊙O外
⊙O内
4
3、已知AB
=3cm,作图说明满足下列要求的图形:
(4)
到点A和点B的距离都小于2cm的所有点组成的图形.
(3)
到点A和B的距离都等于2cm的所有点组成的图形.
(1)
到点A的距离等于2cm的所有点组成的图形.
(2)
到点B的距离等于2cm的所有点组成的图形.
B
A
定义一:
在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆.
固定的端点O叫做圆心,线段OA叫做半径.
1、从运动和集合的观点理解圆的定义:
定义二:圆是到定点的距离等于定长的点的集合.
3、证明几个点在同一个圆上的方法.
要证明几个点在同一个圆上,只要证明这几个点与一个定点的距离相等.
2、点与圆的位置关系:
课堂小结
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
