人教版数学 八年级下册 19.1.1 变量与函数学案
文档属性
| 名称 | 人教版数学 八年级下册 19.1.1 变量与函数学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 00:00:00 | ||
图片预览




文档简介
变量与函数
一、目标认知
学习目标:
1.函数是刻画现实世界中变化规律的非常重要数学模型,对函数概念体会的深入程度是学好函数知识
的关键,在学习过程中一定要紧紧地结合实例体会引入函数概念的意义,紧紧地结合实例体会了解
常量、变量,理解函数的概念,体会“变化与对应”的思想,了解函数的三种表示方法(列表法、解
析式法和图象法)。认真不浮躁地落实基本知识和基本技能。
2.
数学建模思想的体会理解,从分析探索实际问题中的数量关系和变化规律出发,经历体会“找出常
量和变量,建立并表示函数模型,讨论函数模型,解决实际问题”的每个过程细节,提高运用所学
知识分析解决问题的意识。
重点:
函数定义、解析式、自变量取值范围、函数的表示方法
难点:
运用函数定义辨析是否存在函数关系,分析具体材料背景写出函数解析式及自变量取值范围
二、知识要点梳理
知识点一:通过实例体会变量、常量、函数的概念
1、汽车以60千米/时的速度匀速行驶,行驶里程为S千米,行驶时间为t小时,请完成下表:
t/时
1
2
3
4
5
S/千米
60
120
240
300
思考:在上述变化过程中,有两个变量S、t,一个常量速度60,两个变量之间是否有这样的关系:“当其中一个变量取定一个值时,另一个变量就有唯一确定的值与之相对应?”
答案肯定:通过填表可以验证,当这里的两个变量中的任一个变量取定一个可以取的值时,另一个变量都有唯一确定的值与之相对应。
2、每张电影票售价为10元,早场售出150张,日场售出205张,晚场售出310张,三场电影的票房收入各是多少?请完成下表,
时段
早场
日场
晚场
售出票数(张)
150
205
310
收入金额(元)
1500
2050
3100
思考:在上述变化过程中,有两个变量:售出票数和收入金额,一个常量:单价10,两个变量之间是否有这样的关系:“当其中一个变量取定一个值时,另一个变量就有唯一确定的值与之相对应?”
答案肯定:通过填表可以验证,当这里两个变量中的任一个变量随便取定一个可以取的值时,另一个变量都有唯一确定的值与之相对应。
3、在一根弹簧下端悬挂重物,弹簧原长10cm,若每1kg重物使得弹簧伸长0.5cm,请根据不同的重量m,填写对应的弹簧长度L
重量m/kg
1
2
5
8
10
弹簧长度L/cm
10.5
11
12.5
14
15
思考:在上述变化过程中,有两个变量重量和弹簧长度,一些常量弹簧原长、单位重量伸长的数值,两个变量之间是否有这样的关系:“当其中一个变量取定一个值时,另一个变量就有唯一确定的值与之相对应?”
答案肯定:通过填表可以验证,当这里两个变量中的任一个变量随便取定一个可以取的值时,另一个变量都有唯一确定的值与之相对应。
两者之间的关系为:
4、要画一个面积为S的圆,圆的半径r应取多少(保留两位小数)?请完成下表:
圆的面积(S)
10
20
50
100
300
圆的半径(r)
1.78
2.52
3.99
5.64
9.77
思考:在上述变化过程中,有两个变量S、r,一个常量圆周率,两个变量之间是否有这样的关系:“当其中一个变量取定一个值时,另一个变量就有唯一确定的值与之相对应?”
答案肯定:通过填表可以验证,当这里两个变量中的任一个变量随便取定一个可以取的值时,另一个变量都有唯一确定的值与之相对应!
两者之间的关系为:
5、用10m长的绳子围成长方形,根据长方形一边的长度,观察长方形的另一边的长度和面积如何变化。请思考完成下表:
长方形的一边长x/m
2.5
3
3.5
4
4.5
2
1.5
1
0.5
长方形的另一边长y/m
2.5
2
1.5
1
0.5
3
3.5
4
4.5
长方形的面积S/m2
6.25
6
5.25
4
2.25
6
5.25
4
2.25
思考:在上述变化过程中,有三个变量长方形的一边长、另一边长、面积,一个常量长方形的周长10,其中每两个变量之间是否都有这样的关系:“当其中一个变量取定一个值时,另一个变量就有唯一确定的值与之相对应?”
答案不一定:通过填表可以验证,每两个变量之间的关系可分两种情况:(1)一边长与另一边长之间,其中任一个变量取定一个可以取的值时,另一个变量都有唯一确定的值与之相对应。两者之间的关系式为:y=5-x;(2)一边长与面积或另一边长与面积之间,其中当前一个变量随便取定一个可以取的值时,后一个变量都有唯一确定的值与之相对应。两者之间的关系式分别为:S=x(5-x),S=y(5-y);但反过来不满足该规律,例如当面积为5.25m时,长方形的一边长可以为:3.5或1.5,不唯一。
知识点二:函数的定义
在我们身边的各种变化中,有各种变化的量和不变化的量,在两个变量之间有一种不是一定存在的关系,但是非常普遍存在的关系就是:“当其中一个变量随便取定一个值时,另一个变量都有唯一确定的值与之相对应!”也就是说普遍的两个变量之间都存在相互对应的关系!
函数定义:
一般地,在一个变化过程中.
如果有两个变量
x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说
x是自变量(independent
variale),y是x的函数(function),如果当x=a时y=b,那么b叫做当自变量为a时的函数值。
对于函数的意义,应从以下几个方面去理解:
(1)函数不是数,而是两个变量之间一种对应的关系;
(2)对于变量x允许取的每一个值,集合在一起组成了x的取值范围。
(3)判断两个变量之间是否有函数关系不仅要看它们之间是否有关系式,还要看对于x允许取的每一个
值,y是否都有唯一确定的值与它相对应。
(4)两个函数是同一函数至少具备两个条件:①函数关系式相同(或变形后相同);②自变量x的取值
范围相同。否则,就不是相同的函数。而其中函数关系式相同与否比较容易注意到,自变量x的取
值范围有时容易忽视,这点应注意。
知识点三:自变量取值范围的确定
使函数有意义的自变量的取值的全体实数叫自变量的取值范围。自变量的取值范围的确定方法:
首先,要考虑自变量的取值必须使解析式有意义。
⑴
当解析式是整式时,自变量的取值范围是全体实数;
⑵
当解析式是分式时,自变量的取值范围是使分母不为零的实数;
⑶
当解析式是二次根式时,自变量的取值范围是使被开方数不小于零的实数;
⑷
当解析式中含有零指数幂或负整数指数幂时,自变量的取值应使相应的底数不为零。
其次,当解析式表示实际问题时,自变量的取值必须使实际问题有意义。
知识点四:函数值
对于自变量在取值范围内的一个确定的值,比如当时,函数有唯一确定的对应值,这个对应值叫做的函数值,简称函数值。
注意:对于每个确定的自变量值,函数值是唯一的,但反过来,可以不唯一,即一个函数值对应的自变量可以是多个。比如:中,当函数值为4时,自变量的值为。
知识点五:函数的几种表达方式:
变量间的单值对应关系有多种表示方法,常见的有以下三种:
(1)解析式法:用来表示函数关系的等式叫做函数关系式,也称函数的解析式。
注:函数关系式是等式;等式右边的代数式中的变量是自变量,等式左边的一个字母表示自变量的函数;没有特殊说明,自变量x的取值范围是使解析式有意义的所有实数。
(2)列表法:函数关系用一个表格表达出来的方法,例如:前面的五个实例均是用列表法表示的函数;
(3)图像法:用图象表达两个变量之间的关系。
注:有些问题可三种方法兼用,如S=60t,但有些问题只能用某一种方法,如每天的气温变化,只能用图象记录(自动测温仪)。
知识点六:函数的图象
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象。
注:函数的解析式是一个二元方程,这个方程的解分别是这个函数图象上点的横坐标、纵坐标;函数图象的画法:列表、描点、连线。
三、规律方法指导
1.学习函数时,要注意区分常量与变量,函数与函数值等概念,例如:,是随的变化而变化的量,变量是变量的函数,2是常量;函数值是自变量所对应的某个具体数值,一个函数可能有许多不同的函数值,例如当时,函数的函数值等于;当时,函数的函数值等于。
2.函数的图象以几何形式直观地表示变量间的单值对应关系,是研究函数的重要工具。学习函数的图
象不仅要了解它的一般意义和作法,更重要的是了解其中包含的数形结合地研究问题的思想,学习
如何使用这种工具讨论函数。
类型一:函数概念辨析
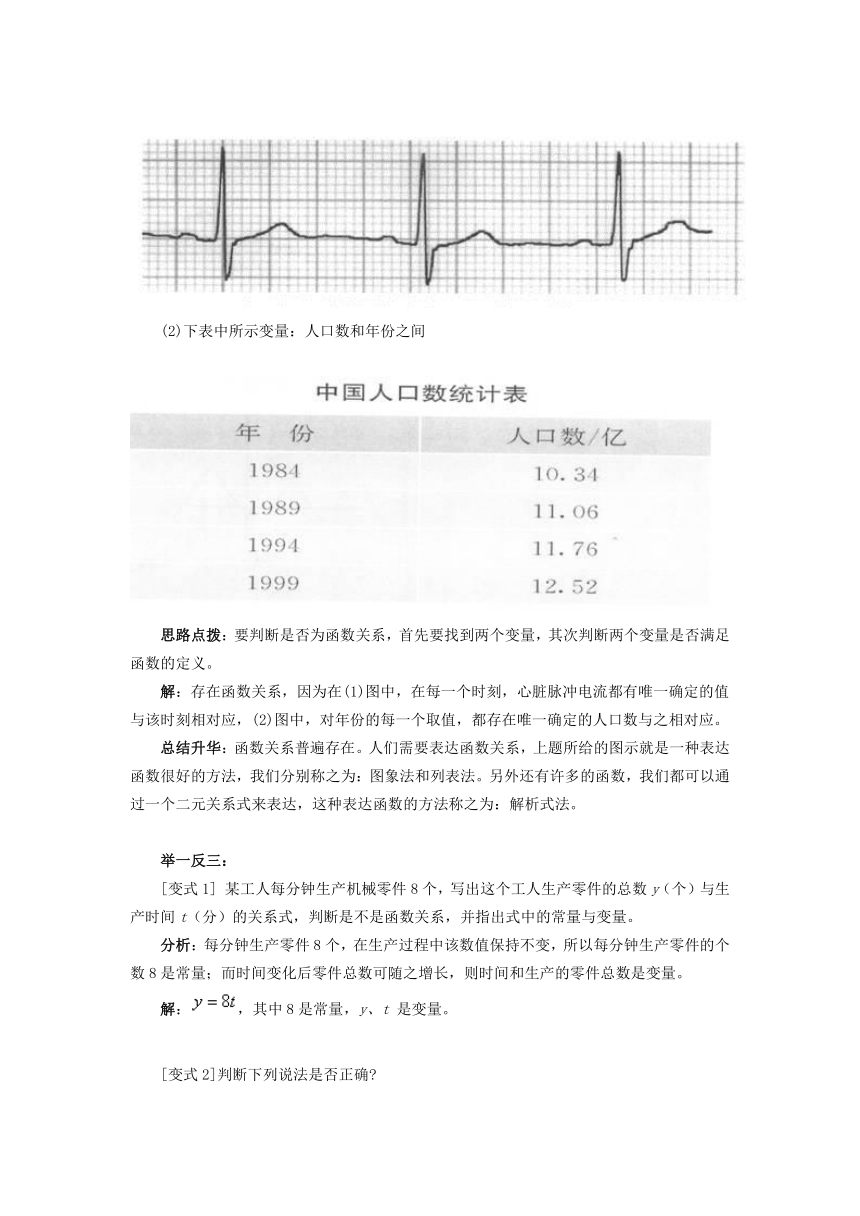
1.判断下列材料中所给的两个变量之间是否存在函数关系?
(1)心电图中的变量:心脏脉冲电流值和时间
(2)下表中所示变量:人口数和年份之间
思路点拨:要判断是否为函数关系,首先要找到两个变量,其次判断两个变量是否满足函数的定义。
解:存在函数关系,因为在(1)图中,在每一个时刻,心脏脉冲电流都有唯一确定的值与该时刻相对应,(2)图中,对年份的每一个取值,都存在唯一确定的人口数与之相对应。
总结升华:函数关系普遍存在。人们需要表达函数关系,上题所给的图示就是一种表达函数很好的方法,我们分别称之为:图象法和列表法。另外还有许多的函数,我们都可以通过一个二元关系式来表达,这种表达函数的方法称之为:解析式法。
举一反三:
[变式1]
某工人每分钟生产机械零件8个,写出这个工人生产零件的总数y(个)与生产时间t(分)的关系式,判断是不是函数关系,并指出式中的常量与变量。
分析:每分钟生产零件8个,在生产过程中该数值保持不变,所以每分钟生产零件的个数8是常量;而时间变化后零件总数可随之增长,则时间和生产的零件总数是变量。
解:,其中8是常量,y、t
是变量。
[变式2]判断下列说法是否正确?
(1)
3x+l是x的函数;
(2)函数y=x与是相同的函数
(3)若y是x的函数,则y的值肯定随x值的改变而改变;
解:(1)说法正确,通过函数定义可以验证,对x的每一个确定取值3x+l都有唯一确定的值与之相对应;
(2)说法不正确,尽管第二个函数经过化简之后解析式与第一个函数相同,但是它们自变量的取值范围是不同的;
(3)说法不正确,比如函数y=x0,随x的变化y的值恒定不变。
[变式3]判断下列关系式和图象中,其中y是否是x的函数?
(1)
(2)
(3)
(4)
(5)
解:
(1),
y是x的函数,因为根据函数定义,对每一个x的可取值都存在唯一确定的y值与之相对应。同样根据函数的定义可验证,y不是x的函数
(2)只有第二个关系式y不是x的函数,其它三个关系式y都是x的函数,理由同上;
(3)y是x的函数,理由同上;
(4)y是x的函数,理由同上;
(5)y不是x的函数,因为由图可以看出,有许多x值都与两个y值相对应。
[变式4]用长为10
cm的绳子围成一个长方形,其中长方形的一条边长是xcm,这个长方形的面积Scm2,判断填空:
这里_____是常量,_____是变量,变量间是否存在函数关系?若存在,其中_____是_____的函数,你是否能说明理由?是否能选择适当的方法表达该函数关系?
解:周长10是常量,边长x和面积s是变量,面积是边长x的函数,因为对于边长x的每一个取值,面积s都有唯一确定的值与之相对应,但反之不成立,即x不是s的函数,用解析式法表达该函数关系:s=x(5-x),其中x的取值范围是0<x<5.
思考:若在上述函数解析式后不加上自变量x的取值范围,函数解析式还能否完整表达背景材料中的函数关系呢?
注:(1)当用解析式表达函数关系时,一定要关注自变量的取值范围;
(2)确定自变量取值范围时,不仅要考虑函数解析式有意义,而且还要注意问题的实际意义;
(3)约定:在我们今后所给定的函数解析式中,若没有特别说明,都默认自变量取值范围为使解析式有意义的所有实数。
类型二:自变量的取值范围
2.求下列函数中自变量x的取值范围。
(1);(2);(3)。
思路点拨:(1)要使分式有意义,则分母,所以;(2)要使被开方数有意义,则,所以;(3)分母且,则有。
解:(1)自变量的取值范围是的实数;
(2)自变量的取值范围是;
(3)自变量的取值范围是。
总结升华:自变量的取值范围必须使整个解析式有意义。
举一反三:
[变式]求函数的自变量的取值范围。
解:要使函数有意义,则x要符合:
即:或
解方程组得自变量取值是或。
类型三:函数表示方法的理解
3.已知,(1)写成y是x的函数形式;(2)写成x是y的函数形式。
思路点拨:y是x的函数形式,就是用含的代数式去表示,x是y的函数形式就是用含的代数式表示,这便是函数的表示方法之一——解析式法,但要使函数解析式有意义。
解析:(1)由可知,又
,所以。
综上得:且。同理得:且
由,去分母有:,移项得,
整理成y是x的函数为(且)。
(2)同理,写成x是y的函数为(且)。
总结升华:函数表示方法有三种:解析式法,图象法和列表法。当用解析式法表示时,通常表示为y是x的函数,但x也可以是y的函数,只要满足函数的定义。
举一反三:
[变式1]写出下列函数关系式:
(1)等腰三角形的底角的度数y°与顶角度数x°之间的关系为______;
(2)某礼堂共有25排座位,第一排有20个座位,后面每排比前一排多1个座位,则每排座位数y与这排的
排数x的关系为_____·
解;(1)
(2)y=x+19
(0<x<26,且x为自然数)
[变式2]已知等腰三角形周长为12cm,若底边长为y
cm,一腰长为x
cm。(1)确定y与x的函数关系式;(2)确定x的取值范围;(3)画出函数图象。
分析:利用等腰三角形周长公式可以写出函数关系式,再利用两边之和大于第三边可以确定x的取值范围,根据腰长与底长的列表可以画出图象。
解:(1)因为,所以。
(2)因为有,所以,即;
又因为,所以,即,
故自变量x的取值范围是。
(3)①列表:
x
3
4
5
5.5
6
y
6
4
2
1
0
②描点,画图(如图所示):
总结升华:要注意三边组成一个三角形的条件,即符合两边之和大于第三边,避免出现的错误。画函数图象时,通常边界值有时也可以取,一般是在范围内的点用实心点,不在范围内的点用空心点。
类型四:函数值
4.设函数,已知当时,,求当时x的值。
思路点拨:利用时可以先求出a值,再把a值代入时的函数中,便可求出x的值。
解:根据题意有,则。
所以有,则。
总结升华:了解常量、变量、函数的意义,会分辨常量与变量,自变量与函数值之间的联系。
举一反三:
[变式1]
求当时,函数的函数值。
分析:自变量x的值一定时,求函数值时只要把x的值代入解析式即可。
解:当时,有。
[变式2]
已知函数,当x为何值时,函数值是正数、0、负数?
分析:已知函数解析式,可分别令函数值为正数、0、负数,即可求x的值。
解:当y为正数时,即,则;
当y为0时,即,则;
当y为负数时,即,则。
所以当时,函数值为正数,当时,函数值为0;当时,函数值为负数。
总结升华:本题的目的是巩固函数值概念,加强对函数值概念的理解。
类型五:函数的综合应用
5.
一辆汽车由A地驶向相距240千米的B地,它的平均速度为30千米/时,求汽车距B地的路程s(千米)与行驶时间t(时)之间的函数关系式,并画出这个函数图象。
思路点拨:路程=速度×时间.
解:由题意可知s=240-30t(0≤
t
≤8).
列表:
t
0
2
4
8
s
240
180
120
0
画函数图象如图所示.
总结升华:画图象前先列表,令t为某值,代入函数式后可求出相应函数值.
举一反三:
[变式1]
已知在等腰△ABC中,AB=AC,根据下列条件,求y与x的函数解析式及自变量x的取值范围.
(1)底角度数为x°,顶角度数为y°;
(2)腰长为x,底边长为y,周长为8.
解:(1)由等腰三角形的特点及内角和定理可知;
(2)由周长=2×腰长+底长可知,.
[变式2]
某公园集体门票的收费标准是:20人以内(含20人),每人25元,超过20人的部分,每人10元.
(1)写出应收门票费y(元)与进园人数x(人)(x≥20)之间的函数关系式.
(2)利用(1)中的关系式计算:某旅游团有54人去该公园观赏,购买门票花了多少钱?
分析:20人以内应收费为25×人数(元),当进园人数为x(x≥20)人时,门票费y元。则等于20人的门票费加上超过部分人数购买的门票费.
解:(1)根据题意有,
整理得(x为整数,且x≥20).
(2)根据,当x=54时,有y=10×54+300=840(元),
即54人进园购票费用为840元.
[变式3]
如下图中各图形是由若干皮球摆成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)个皮球,每个图案皮球总数是s,按照所给规律写出总数s与皮球个数n之间的关系式.
分析:通过所绘图案可得:随着每条边包含的皮球数的增多,图案的皮球总数s也在增大.且有:n=2,S=3;n=3,S=6;n=4,S=9。n每增加1时,S增加3。因此,可猜想s=3+3(n-2),
可用n=2,S=3;n=3,S=6;n=4,S=9验证关系式,结论正确。
解:关系式为.
总结升华:通过本题,可考查观察、探索、发现问题的综合能力.
