人教版八年级下册数学 18.1 平行四边形 复习课件 (共31张PPT)
文档属性
| 名称 | 人教版八年级下册数学 18.1 平行四边形 复习课件 (共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 750.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 17:50:55 | ||
图片预览

文档简介
(共31张PPT)
18.1
平行四边形
复习课
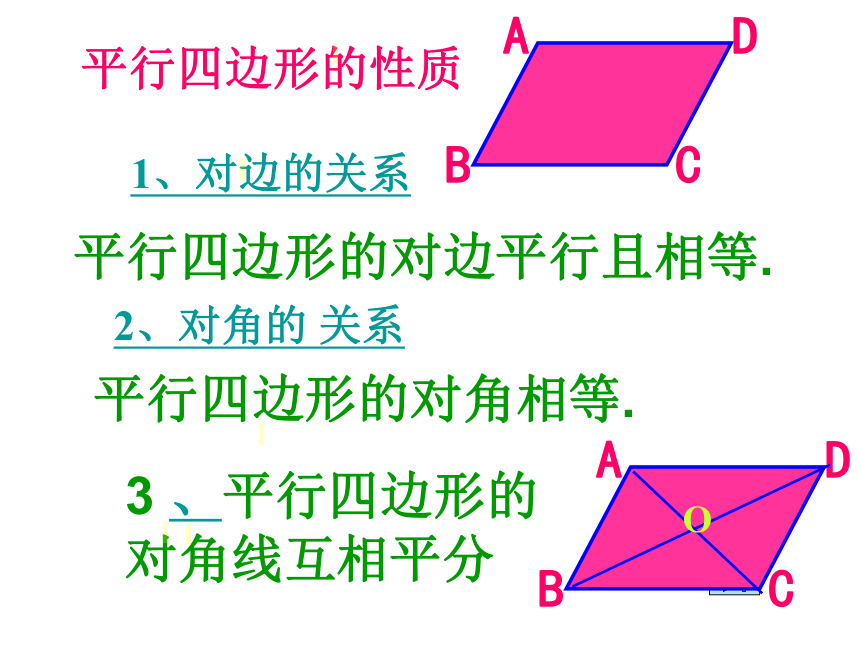
平行四边形的性质
1、对边的关系
2、对角的
关系
平行四边形的对边平行且相等.
平行四边形的对角相等.
A
A
B
C
D
A
B
C
D
O
3
、平行四边形的对角线互相平分
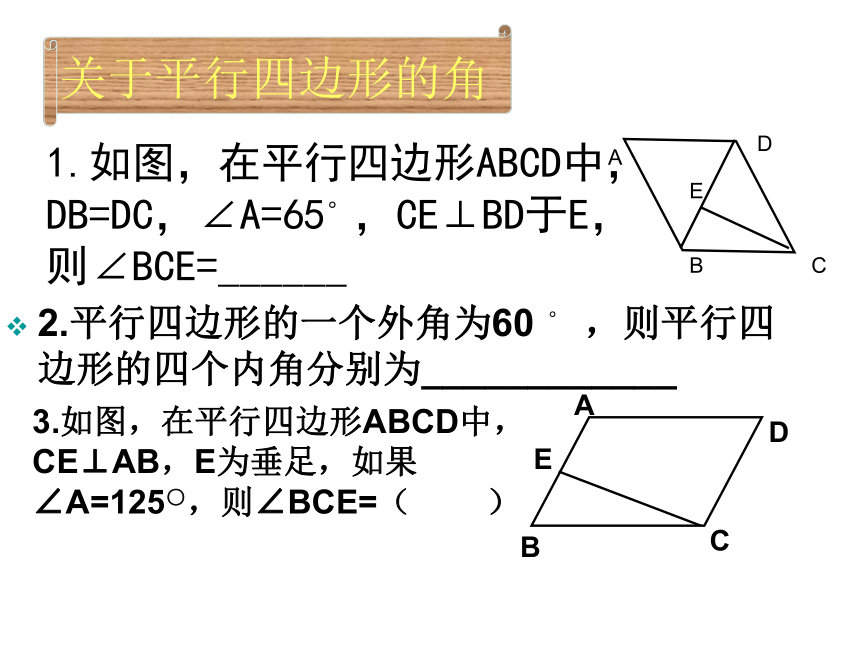
关于平行四边形的角
1.如图,在平行四边形ABCD中,DB=DC,∠A=65°,CE⊥BD于E,则∠BCE=______
A
B
C
D
E
2.平行四边形的一个外角为60
°
,则平行四边形的四个内角分别为____________
3.如图,在平行四边形ABCD中,CE⊥AB,E为垂足,如果∠A=125○,则∠BCE=(
)
A
B
C
D
E
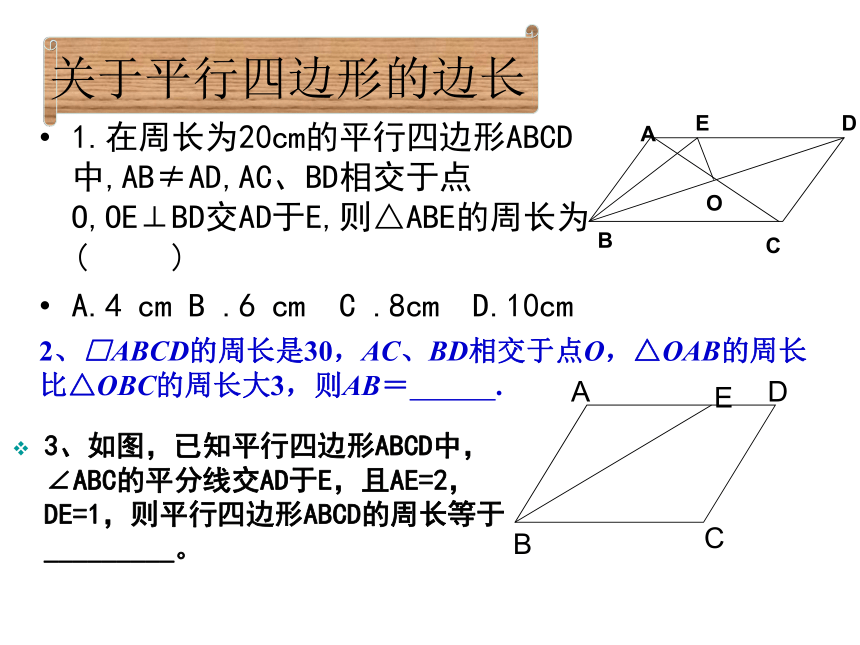
1.在周长为20cm的平行四边形ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为(
)
A.4
cm
B
.6
cm
C
.8cm
D.10cm
A
B
C
D
O
E
关于平行四边形的边长
2、□ABCD的周长是30,AC、BD相交于点O,△OAB的周长比△OBC的周长大3,则AB=
.
3、如图,已知平行四边形ABCD中,∠ABC的平分线交AD于E,且AE=2,DE=1,则平行四边形ABCD的周长等于_________。
A
B
C
D
E
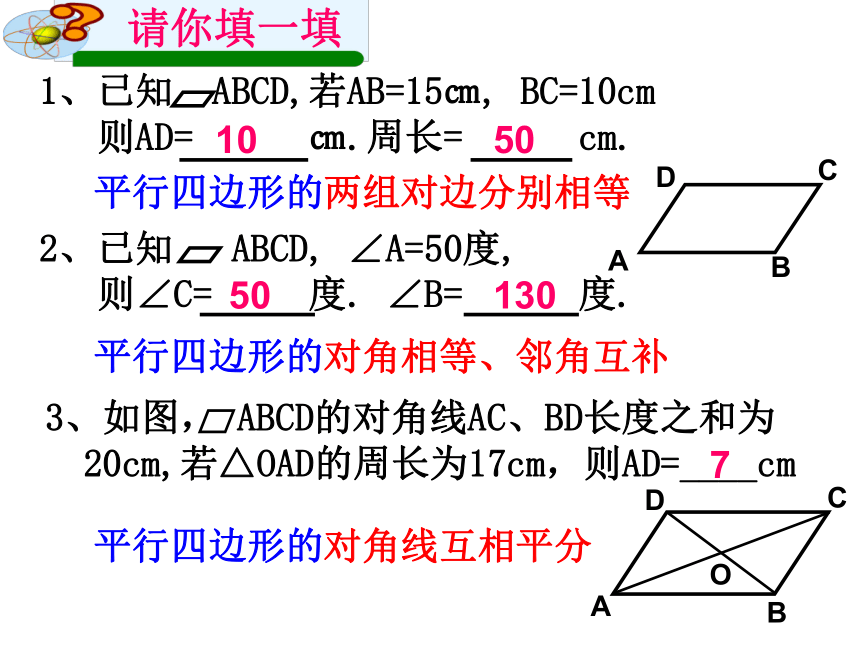
1、已知
ABCD,若AB=15㎝,
BC=10cm
则AD=
㎝.周长=
cm.
请你填一填
50
130
平行四边形的对角相等、邻角互补
10
50
平行四边形的两组对边分别相等
A
B
C
D
O
平行四边形的对角线互相平分
2、已知
ABCD,
∠A=50度,
则∠C=
度.
∠B=
度.
A
B
C
D
3、如图,
ABCD的对角线AC、BD长度之和为
20cm,若△OAD的周长为17cm,则AD=____cm
7
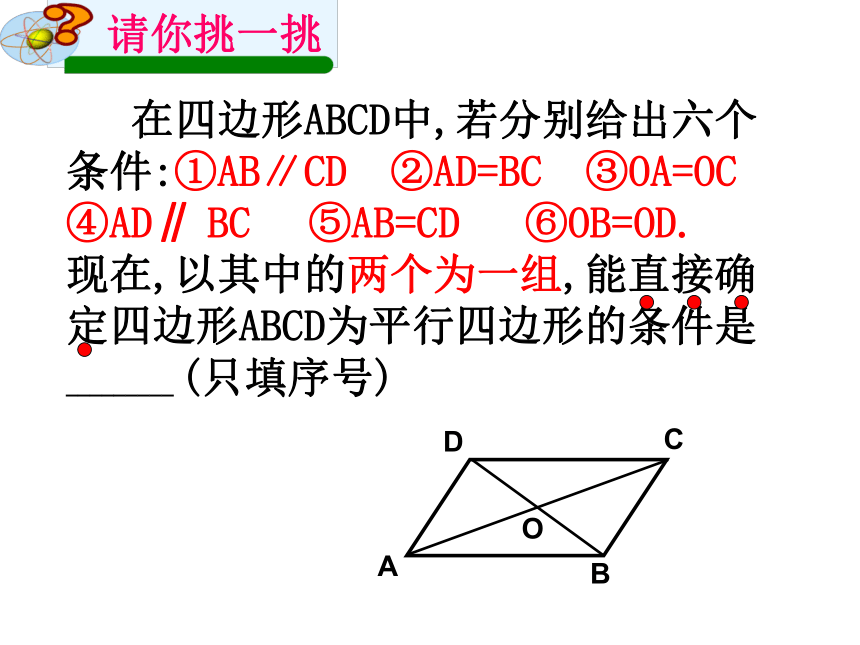
在四边形ABCD中,若分别给出六个条件:①AB∥CD
②AD=BC
③OA=OC
④AD∥
BC
⑤AB=CD
⑥OB=OD.
现在,以其中的两个为一组,能直接确定四边形ABCD为平行四边形的条件是
_________
(只填序号)
请你挑一挑
A
B
C
D
O
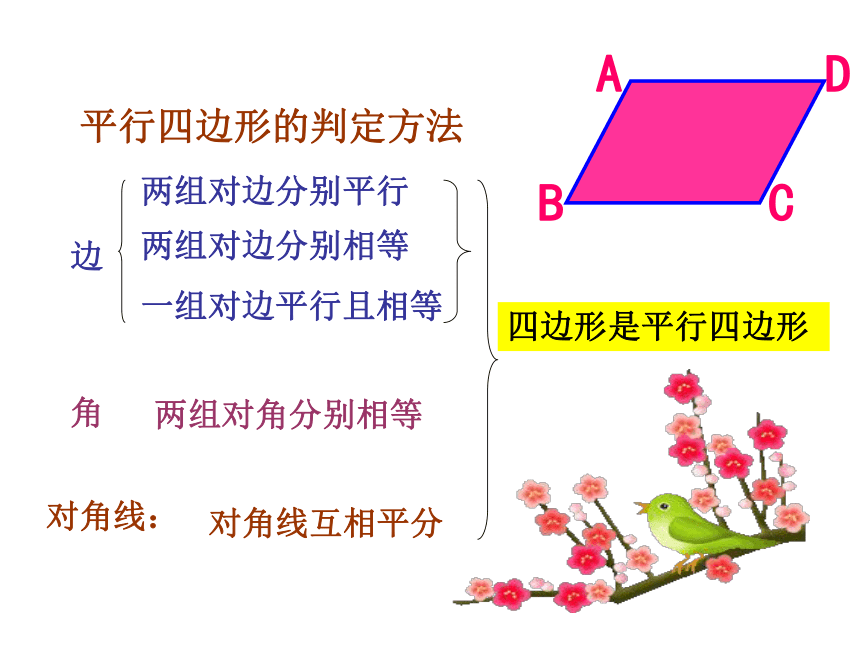
两组对边分别相等
两组对角分别相等
对角线互相平分
两组对边分别平行
平行四边形的判定方法
一组对边平行且相等
四边形是平行四边形
边
角
对角线:
A
B
C
D
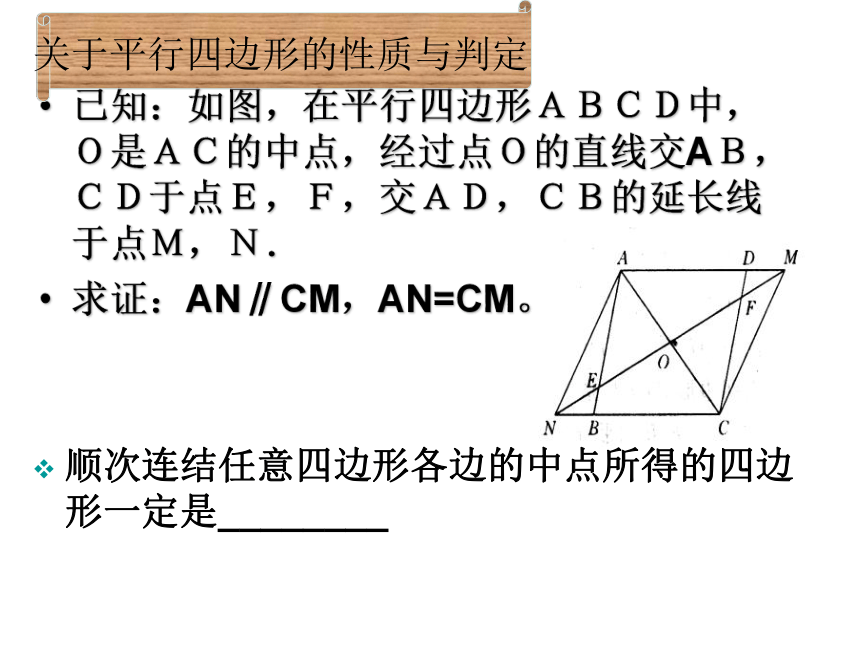
已知:如图,在平行四边形ABCD中,O是AC的中点,经过点O的直线交AB,CD于点E,F,交AD,CB的延长线于点M,N.
求证:AN∥CM,AN=CM。
关于平行四边形的性质与判定
顺次连结任意四边形各边的中点所得的四边形一定是________
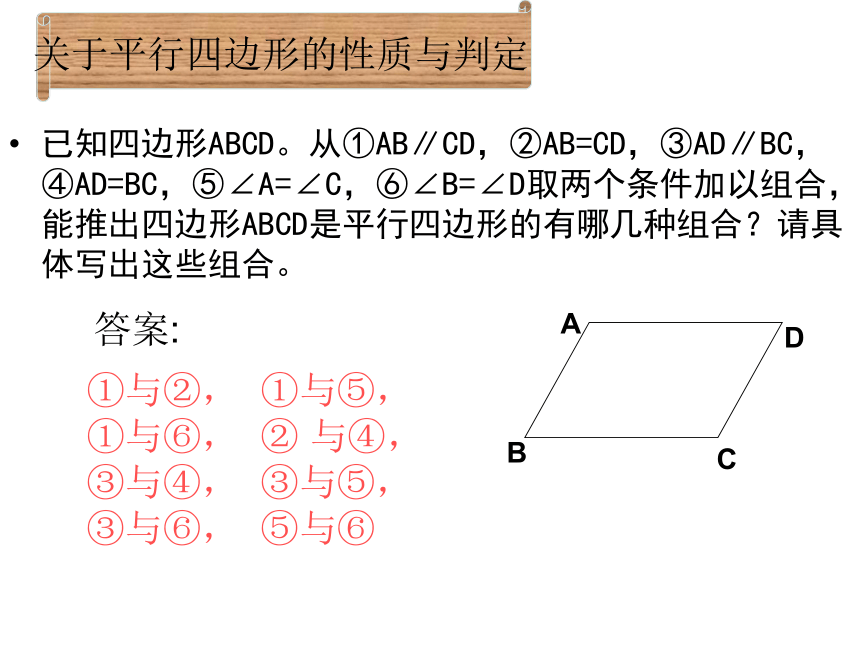
已知四边形ABCD。从①AB∥CD,②AB=CD,③AD∥BC,④AD=BC,⑤∠A=∠C,⑥∠B=∠D取两个条件加以组合,能推出四边形ABCD是平行四边形的有哪几种组合?请具体写出这些组合。
A
B
C
D
答案:
①与②,
①与⑤,
①与⑥,
②
与④,
③与④,
③与⑤,
③与⑥,
⑤与⑥
关于平行四边形的性质与判定
M
D
C
B
A
M
D
C
B
A
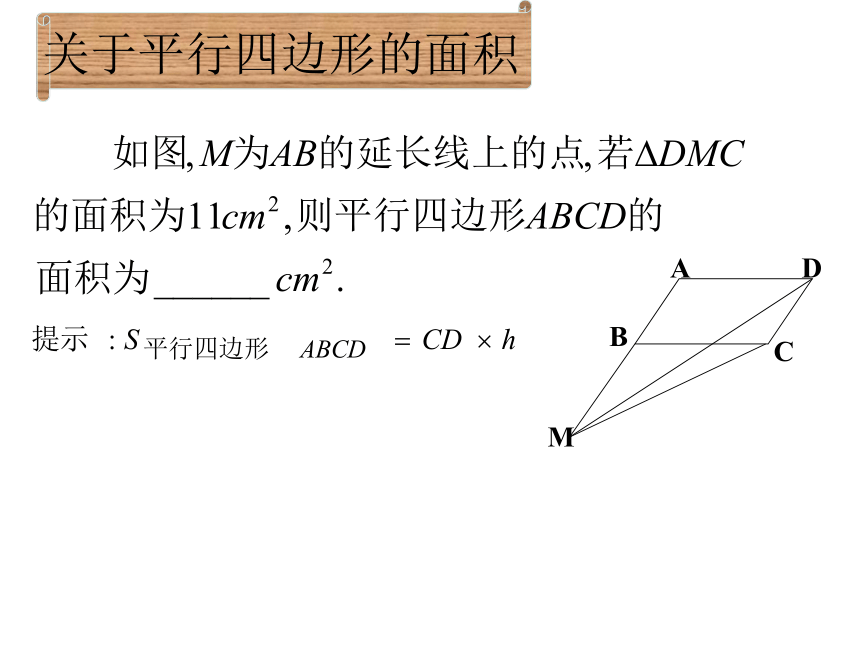
关于平行四边形的面积
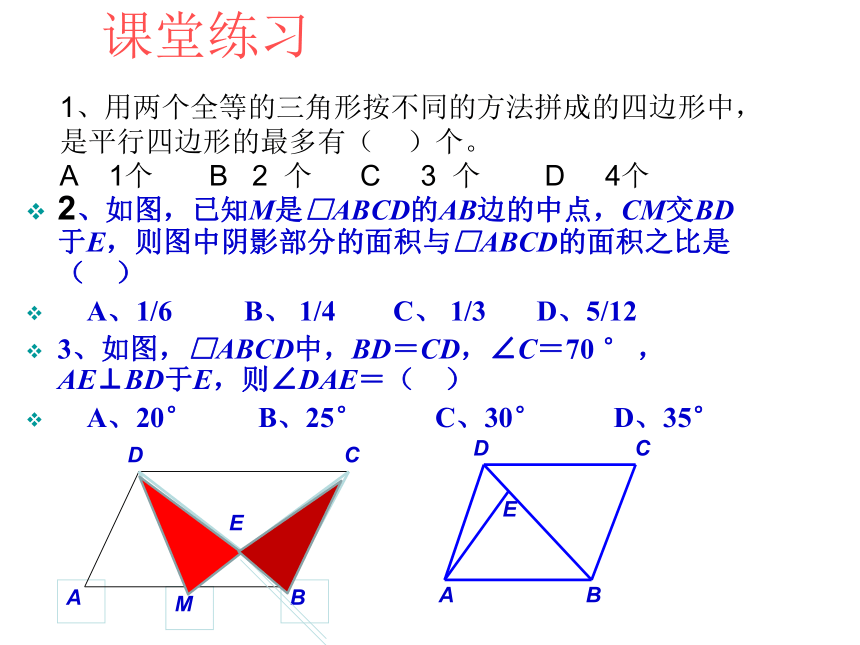
课堂练习
1、用两个全等的三角形按不同的方法拼成的四边形中,是平行四边形的最多有(
)个。
A
1个
B
2
个
C
3
个
D
4个
2、如图,已知M是□ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与□ABCD的面积之比是(
)
A、1/6
B、
1/4
C、
1/3
D、5/12
3、如图,□ABCD中,BD=CD,∠C=70
°
,AE⊥BD于E,则∠DAE=(
)
A、20°
B、25°
C、30°
D、35°
A
B
C
D
E
M
A
B
C
D
E
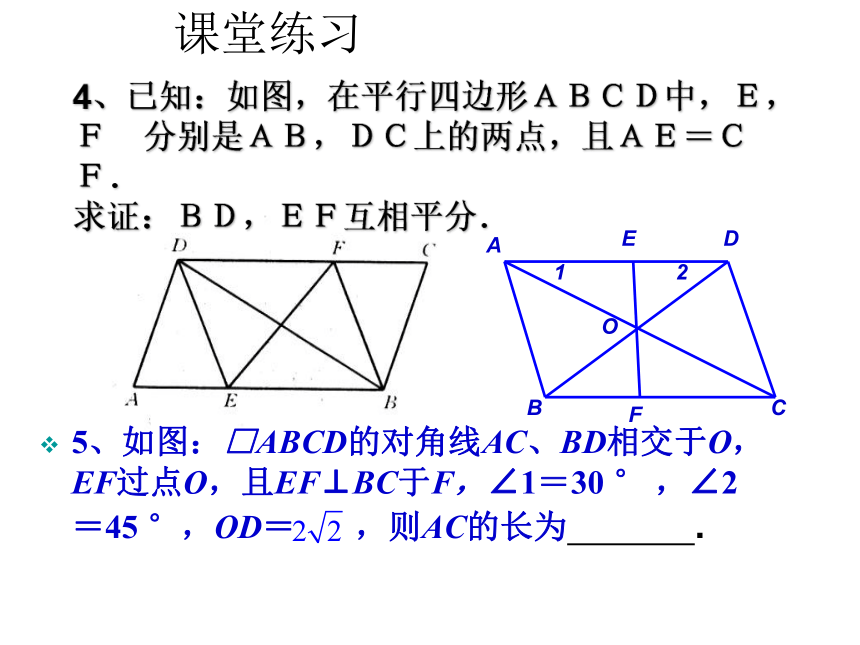
课堂练习
4、已知:如图,在平行四边形ABCD中,E,F
分别是AB,DC上的两点,且AE=CF.
求证:BD,EF互相平分.
5、如图:□ABCD的对角线AC、BD相交于O,EF过点O,且EF⊥BC于F,∠1=30
°
,∠2=45
°,OD=
,则AC的长为
.
A
B
C
D
E
F
O
1
2
课堂练习
6、在□ABCD中,AB=6,AD=8,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内的点E处,如果AE过BC的中点O,则□ABCD的面积等于(
)
A、48
B、
C、
D、
A
B
C
D
E
O
x
1
2
3
4
5
0
1
2
3
B
C
D
A
y
课堂练习
如图,平行四边形ABCD中,A、B、C三点坐标分别是A(3,3),B(1,1),C(4,1)。
(1)求点D的坐标。
(2)将平行四边形向下平移2个单位长度,则A′、B′、C′、D′各点的坐标分别是多少?
(3)在(2)的前提下,再将平行四边形向左平移1个单位,则A″、B″、C″、D″的坐标又是多少?
(4)求平行四边形ABCD的面积。
A′
B′
C′
D′
A″
B″
C″
D″
解题思维分析小结
四边形的概念是建立在三角形的基础上,是知识的扩展和深化,研究它的性质,常常是将四边形转化为若干三角形(即三角形三角形奠基法),通过三角形的性质来研究,或者是通过辅助线将四边形转化为三角形或平行四边形来讨论。至于矩形、菱形、正方形的性质是在平行四边形的基础上扩充的,它们的判定方法也是在平行四边形的基础上增加一些特定的条件,平行四边形的有关性质定理是证明两线段相等、两角相等、两直线平行或垂直的重要依据。
1、下列条件中,不能判定四边形ABCD是平行四边形的是(
)
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180
,∠B+∠C=180
∠A+∠B=180
,∠C+∠D=180
A
B
C
D
D
已知:
ABCD中,直线MN//AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。
探究应用一
☆找平行四边形
如图,在
ABCD中,E、F、G、H
分别是各边上的点,且AE=CF,BG=DH。
求证:EF与GH互相平分。
A
B
C
D
H
E
G
F
探究应用二
☆构造平行四边形
已知:AD为△ABC的角平分线,DE∥AB
,在AB上截取BF=AE。
求证:EF=BD
1
2
3
小试牛刀
如图,AD、BC垂直相交于点O,AB∥CD,BC=8,AD=6,求AB+CD的长?
小试牛刀
O
A
D
C
B
已知:如图,在平行四边形ABCD的周长为20cm,O是对角线AC和BD的交点
(1)若△ABC的周长是7cm,求OC的长
(2)若△OAB的周长比△OBC的周长短4cm,求AB的长
A
B
C
D
O
4.如图
四边形
ABCD和四边形BEDF都是平行四边形,
请你说明(1)
AE=CF的理由
E
D
A
C
B
F
O
变式:如图
已知
四边形
ABCD都是平行四边形,
AE=CF,请你说明四边形BEDF是平行四边形
E
D
A
C
B
F
知识运用
例1:已知E、F是
ABCD边AD、BC的中点,
求证:BE=DF。
例2:已知点D、E、F分别在
ABC的边BC、AB、AC上,且DE
AF,DE=AF,G在FD的延长线上,DG=DF。
求证:AG与ED互相平分。
拓展训练1
1.如图,若□ABCD与□EBCF关于
直线BC对称,∠ABE=90°,则∠F?=_____°.
4.如图(3),在□ABCD中,E、F分别为AD、BC边上的一点,若再增加一个条件
_____________,就可推得BE
=
DF.
链接中考
2、已知
ABCD,若AC=20㎝,BD=16cm,OA=___cm,OB=___cm.
8
10
3、(浙江金华中考题)国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB//EF//DC,BC//GH//AD,那么下列说法中错误的是(
)
A.红花、绿花种植面积一定相等
B.紫花、橙花种植面积一定相等
C.红花、蓝花种植面积一定相等
D.蓝花、黄花种植面积一定相等
C
DE=BF
45
或BE∥DF
或AE=CF
□ABCD的周长为32cm,
∠ABC的角平分线交边AD所在直线于点E,且AE:ED
=3:2,则AB=______________.
6cm或12cm
链接中考
A
B
C
D
E
A
B
C
D
E
3x
3x
2x
x
2x
3x
拓展提高
如图,已知AB=AC,B是AD的中点,E是AB的中点.
求证:CD=2CE.
E
D
C
B
A
F
通过这节课的复习,
你又增加了哪些收获?
能与大家一起分享吗?
丰
收
园
x
y
O
1
2
3
-1
-2
7
2
1
3
-1
-2
-3
-3
4
如图,Rt△OAB的两条直角边在坐标轴上,已知点A(0,2),点B(3,0),则以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标为_________________。
A
B
O
-4
初露锋芒
(3,2)
(3,-2)
(-3,2)
x
y
O
1
2
3
-1
-2
2
1
3
-1
-2
-3
-3
4
在上题中,再作一条直线L,解析式为y=-2x+2,设点M为直线L上一点,过点M作AB的平行线,交y轴于点N,是否存在这样的点M,使得以M、N、A、B为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由。
A
B
O
L
-4
大显身手
x
y
O
1
2
3
-1
-2
2
1
3
-1
-2
-3
-3
4
A
B
O
-4
6
5
4
-4
M
N
N
M
y=-2x+2
(3,-4)
(-3,8)
MN在AB下方
MN在AB上方
18.1
平行四边形
复习课
平行四边形的性质
1、对边的关系
2、对角的
关系
平行四边形的对边平行且相等.
平行四边形的对角相等.
A
A
B
C
D
A
B
C
D
O
3
、平行四边形的对角线互相平分
关于平行四边形的角
1.如图,在平行四边形ABCD中,DB=DC,∠A=65°,CE⊥BD于E,则∠BCE=______
A
B
C
D
E
2.平行四边形的一个外角为60
°
,则平行四边形的四个内角分别为____________
3.如图,在平行四边形ABCD中,CE⊥AB,E为垂足,如果∠A=125○,则∠BCE=(
)
A
B
C
D
E
1.在周长为20cm的平行四边形ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为(
)
A.4
cm
B
.6
cm
C
.8cm
D.10cm
A
B
C
D
O
E
关于平行四边形的边长
2、□ABCD的周长是30,AC、BD相交于点O,△OAB的周长比△OBC的周长大3,则AB=
.
3、如图,已知平行四边形ABCD中,∠ABC的平分线交AD于E,且AE=2,DE=1,则平行四边形ABCD的周长等于_________。
A
B
C
D
E
1、已知
ABCD,若AB=15㎝,
BC=10cm
则AD=
㎝.周长=
cm.
请你填一填
50
130
平行四边形的对角相等、邻角互补
10
50
平行四边形的两组对边分别相等
A
B
C
D
O
平行四边形的对角线互相平分
2、已知
ABCD,
∠A=50度,
则∠C=
度.
∠B=
度.
A
B
C
D
3、如图,
ABCD的对角线AC、BD长度之和为
20cm,若△OAD的周长为17cm,则AD=____cm
7
在四边形ABCD中,若分别给出六个条件:①AB∥CD
②AD=BC
③OA=OC
④AD∥
BC
⑤AB=CD
⑥OB=OD.
现在,以其中的两个为一组,能直接确定四边形ABCD为平行四边形的条件是
_________
(只填序号)
请你挑一挑
A
B
C
D
O
两组对边分别相等
两组对角分别相等
对角线互相平分
两组对边分别平行
平行四边形的判定方法
一组对边平行且相等
四边形是平行四边形
边
角
对角线:
A
B
C
D
已知:如图,在平行四边形ABCD中,O是AC的中点,经过点O的直线交AB,CD于点E,F,交AD,CB的延长线于点M,N.
求证:AN∥CM,AN=CM。
关于平行四边形的性质与判定
顺次连结任意四边形各边的中点所得的四边形一定是________
已知四边形ABCD。从①AB∥CD,②AB=CD,③AD∥BC,④AD=BC,⑤∠A=∠C,⑥∠B=∠D取两个条件加以组合,能推出四边形ABCD是平行四边形的有哪几种组合?请具体写出这些组合。
A
B
C
D
答案:
①与②,
①与⑤,
①与⑥,
②
与④,
③与④,
③与⑤,
③与⑥,
⑤与⑥
关于平行四边形的性质与判定
M
D
C
B
A
M
D
C
B
A
关于平行四边形的面积
课堂练习
1、用两个全等的三角形按不同的方法拼成的四边形中,是平行四边形的最多有(
)个。
A
1个
B
2
个
C
3
个
D
4个
2、如图,已知M是□ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与□ABCD的面积之比是(
)
A、1/6
B、
1/4
C、
1/3
D、5/12
3、如图,□ABCD中,BD=CD,∠C=70
°
,AE⊥BD于E,则∠DAE=(
)
A、20°
B、25°
C、30°
D、35°
A
B
C
D
E
M
A
B
C
D
E
课堂练习
4、已知:如图,在平行四边形ABCD中,E,F
分别是AB,DC上的两点,且AE=CF.
求证:BD,EF互相平分.
5、如图:□ABCD的对角线AC、BD相交于O,EF过点O,且EF⊥BC于F,∠1=30
°
,∠2=45
°,OD=
,则AC的长为
.
A
B
C
D
E
F
O
1
2
课堂练习
6、在□ABCD中,AB=6,AD=8,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内的点E处,如果AE过BC的中点O,则□ABCD的面积等于(
)
A、48
B、
C、
D、
A
B
C
D
E
O
x
1
2
3
4
5
0
1
2
3
B
C
D
A
y
课堂练习
如图,平行四边形ABCD中,A、B、C三点坐标分别是A(3,3),B(1,1),C(4,1)。
(1)求点D的坐标。
(2)将平行四边形向下平移2个单位长度,则A′、B′、C′、D′各点的坐标分别是多少?
(3)在(2)的前提下,再将平行四边形向左平移1个单位,则A″、B″、C″、D″的坐标又是多少?
(4)求平行四边形ABCD的面积。
A′
B′
C′
D′
A″
B″
C″
D″
解题思维分析小结
四边形的概念是建立在三角形的基础上,是知识的扩展和深化,研究它的性质,常常是将四边形转化为若干三角形(即三角形三角形奠基法),通过三角形的性质来研究,或者是通过辅助线将四边形转化为三角形或平行四边形来讨论。至于矩形、菱形、正方形的性质是在平行四边形的基础上扩充的,它们的判定方法也是在平行四边形的基础上增加一些特定的条件,平行四边形的有关性质定理是证明两线段相等、两角相等、两直线平行或垂直的重要依据。
1、下列条件中,不能判定四边形ABCD是平行四边形的是(
)
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180
,∠B+∠C=180
∠A+∠B=180
,∠C+∠D=180
A
B
C
D
D
已知:
ABCD中,直线MN//AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。
探究应用一
☆找平行四边形
如图,在
ABCD中,E、F、G、H
分别是各边上的点,且AE=CF,BG=DH。
求证:EF与GH互相平分。
A
B
C
D
H
E
G
F
探究应用二
☆构造平行四边形
已知:AD为△ABC的角平分线,DE∥AB
,在AB上截取BF=AE。
求证:EF=BD
1
2
3
小试牛刀
如图,AD、BC垂直相交于点O,AB∥CD,BC=8,AD=6,求AB+CD的长?
小试牛刀
O
A
D
C
B
已知:如图,在平行四边形ABCD的周长为20cm,O是对角线AC和BD的交点
(1)若△ABC的周长是7cm,求OC的长
(2)若△OAB的周长比△OBC的周长短4cm,求AB的长
A
B
C
D
O
4.如图
四边形
ABCD和四边形BEDF都是平行四边形,
请你说明(1)
AE=CF的理由
E
D
A
C
B
F
O
变式:如图
已知
四边形
ABCD都是平行四边形,
AE=CF,请你说明四边形BEDF是平行四边形
E
D
A
C
B
F
知识运用
例1:已知E、F是
ABCD边AD、BC的中点,
求证:BE=DF。
例2:已知点D、E、F分别在
ABC的边BC、AB、AC上,且DE
AF,DE=AF,G在FD的延长线上,DG=DF。
求证:AG与ED互相平分。
拓展训练1
1.如图,若□ABCD与□EBCF关于
直线BC对称,∠ABE=90°,则∠F?=_____°.
4.如图(3),在□ABCD中,E、F分别为AD、BC边上的一点,若再增加一个条件
_____________,就可推得BE
=
DF.
链接中考
2、已知
ABCD,若AC=20㎝,BD=16cm,OA=___cm,OB=___cm.
8
10
3、(浙江金华中考题)国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB//EF//DC,BC//GH//AD,那么下列说法中错误的是(
)
A.红花、绿花种植面积一定相等
B.紫花、橙花种植面积一定相等
C.红花、蓝花种植面积一定相等
D.蓝花、黄花种植面积一定相等
C
DE=BF
45
或BE∥DF
或AE=CF
□ABCD的周长为32cm,
∠ABC的角平分线交边AD所在直线于点E,且AE:ED
=3:2,则AB=______________.
6cm或12cm
链接中考
A
B
C
D
E
A
B
C
D
E
3x
3x
2x
x
2x
3x
拓展提高
如图,已知AB=AC,B是AD的中点,E是AB的中点.
求证:CD=2CE.
E
D
C
B
A
F
通过这节课的复习,
你又增加了哪些收获?
能与大家一起分享吗?
丰
收
园
x
y
O
1
2
3
-1
-2
7
2
1
3
-1
-2
-3
-3
4
如图,Rt△OAB的两条直角边在坐标轴上,已知点A(0,2),点B(3,0),则以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标为_________________。
A
B
O
-4
初露锋芒
(3,2)
(3,-2)
(-3,2)
x
y
O
1
2
3
-1
-2
2
1
3
-1
-2
-3
-3
4
在上题中,再作一条直线L,解析式为y=-2x+2,设点M为直线L上一点,过点M作AB的平行线,交y轴于点N,是否存在这样的点M,使得以M、N、A、B为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由。
A
B
O
L
-4
大显身手
x
y
O
1
2
3
-1
-2
2
1
3
-1
-2
-3
-3
4
A
B
O
-4
6
5
4
-4
M
N
N
M
y=-2x+2
(3,-4)
(-3,8)
MN在AB下方
MN在AB上方
