4.1 、势能的变化与机械功课件:22张PPT
文档属性
| 名称 | 4.1 、势能的变化与机械功课件:22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-30 04:56:40 | ||
图片预览







文档简介
(共22张PPT)
有关弹力的知识
压缩的弹簧
有关弹力的知识
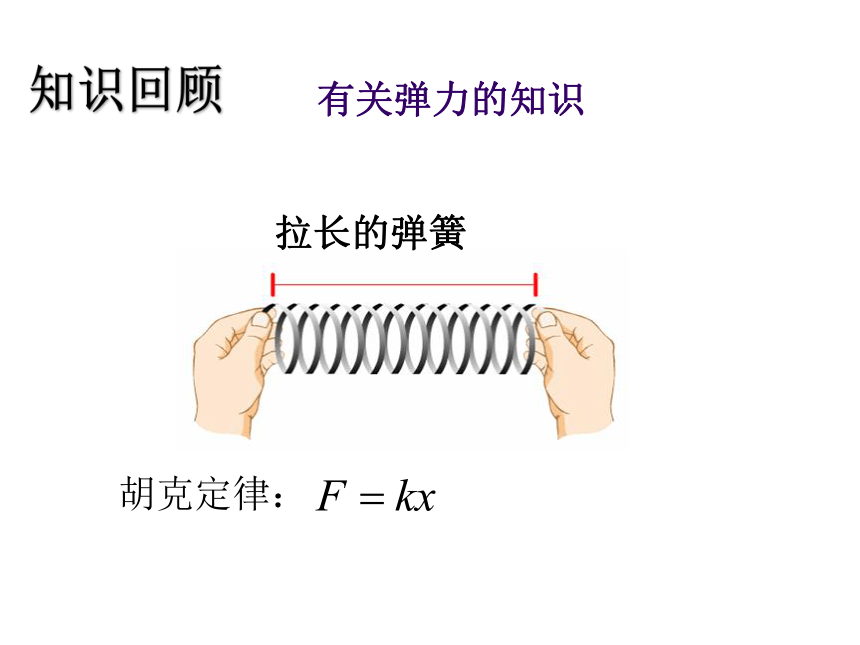
拉长的弹簧
胡克定律:
发生弹性形变的物体的各部分之间,由于有弹力的相互作用而具有的势能叫弹性势能(elastic
potential
energe)
。
本节课我们主要探究弹簧被拉长时的弹性势能的表达式。
重力势能
与高度h有关,且成正比
弹性势能
伸长量l
是正比关系吗
功
弹力与重力的变化规律不一样,弹性势能与重力势能的表达式很可能也不一样。
弹性势能的表达式可能与哪几个物理量有关?
结论:与弹簧的伸长量l
有关
与弹簧的劲度系数k有关
对与同一根弹簧,伸长量l越长,
伸长量l相同,劲度系数k越大,
弹性势能也越大
弹性势能也越大
对于弹力,情况要比重力做功复杂,这是因为当弹簧被拉伸时,弹簧的拉力的大小会随着拉伸距离的增大而增大.也就是说:
弹力做功应该是一个变力做功的问题.
怎样计算拉力所做的功?
把整个运动过程分成很多小段,每个小段中物体的速度的变化比较小,可以用小段中任意一时刻的速度和这一小段时间间隔相乘得到这一小段位移的近似值,然后把各小段位移的近似值相加.当各小段分得非常小的时候,得到的就是匀变速直线运动的位移表达式了.
联想
计算匀加速直线运动位移时曾经用过的方法:
怎样计算这个求和式?
联想
计算匀加速直线运动位移时曾经
用过的方法
怎样计算拉力所做的功?
方法
拉力在全过程中所做的功是
在各小段上,拉力做的功分别是
怎样计算拉力所做的功?
拉力做功的计算方法
方法
拉力所做的功
其中,k是弹簧的劲度系数,
l是弹簧的伸长量或压缩量
弹性势能的表达式
根据我们刚才的推论,当弹簧处于原长、弹性势能值为0时,这个弹簧被拉长L时弹力做的功就等于弹簧被拉长L时弹簧弹性势能的值,所以有
体会功是能量转化的量度.
一、弹性势能
定义:发生弹性形变的物体各部分之间,由于弹力的相互作用而具有的势能.
二、重力势能的表达式:
弹性势能的表达式:
5.5探究弹性势能的表达式
1.在水平面上竖直放置一轻弹簧,有一物体在它的正上方自由落下,在物体压缩弹簧速度减为零时(
)
A.物体的重力势能最大
B.物体的动能最大
C.弹簧的弹性势能最大
D.物体的弹性势能最小
对弹性势能的理解
对弹性势能的理解
3.
如图所示,劲度系数为k的轻质弹簧一端固定,另一端与物块拴接,物块放在光滑水平面上。现用外力缓慢推动物块,将弹簧压缩了长度l,试用图象法求在此过程中外力所做的功。
4.
两弹簧的劲度系数之比为1:2,在弹性限度内的形变量之比为2:1,则它们的弹性势能之比为(
)
A.
1:2
B.
2:1
C.
1:4
D.
4:1
一物体以初速度v0冲向与竖起墙壁相连的轻质弹簧,墙壁与物体间的弹簧被物体压缩,在此过程中,下列说法正确的是:( )
A、物体对弹簧做的功与弹簧的压缩量成正比
B、物体向墙壁移动相同的距离,弹力做的功不相等
C、弹力做正功,弹簧的弹性势能减小
D、弹力做负功,弹簧的弹性势能增加
BCD
对弹性势能的理解
一竖直弹簧下端固定于水平地面上,小球从弹簧的正上方高为h的地方自由下落到弹簧上端,如图所示,经几次反弹以后小球最终在弹簧上静止于某一点A处,则(
)
A.h愈大,弹簧在A点的压缩量愈大
B.弹簧在A点的压缩量与h无关
C.h愈大,最终小球静止在A点时弹簧的弹性势能愈大
D.小球第一次到达A点时弹簧的弹性势能比最终小球静止在A点时弹簧的弹性势能大
B
对弹性势能的理解
有关弹力的知识
压缩的弹簧
有关弹力的知识
拉长的弹簧
胡克定律:
发生弹性形变的物体的各部分之间,由于有弹力的相互作用而具有的势能叫弹性势能(elastic
potential
energe)
。
本节课我们主要探究弹簧被拉长时的弹性势能的表达式。
重力势能
与高度h有关,且成正比
弹性势能
伸长量l
是正比关系吗
功
弹力与重力的变化规律不一样,弹性势能与重力势能的表达式很可能也不一样。
弹性势能的表达式可能与哪几个物理量有关?
结论:与弹簧的伸长量l
有关
与弹簧的劲度系数k有关
对与同一根弹簧,伸长量l越长,
伸长量l相同,劲度系数k越大,
弹性势能也越大
弹性势能也越大
对于弹力,情况要比重力做功复杂,这是因为当弹簧被拉伸时,弹簧的拉力的大小会随着拉伸距离的增大而增大.也就是说:
弹力做功应该是一个变力做功的问题.
怎样计算拉力所做的功?
把整个运动过程分成很多小段,每个小段中物体的速度的变化比较小,可以用小段中任意一时刻的速度和这一小段时间间隔相乘得到这一小段位移的近似值,然后把各小段位移的近似值相加.当各小段分得非常小的时候,得到的就是匀变速直线运动的位移表达式了.
联想
计算匀加速直线运动位移时曾经用过的方法:
怎样计算这个求和式?
联想
计算匀加速直线运动位移时曾经
用过的方法
怎样计算拉力所做的功?
方法
拉力在全过程中所做的功是
在各小段上,拉力做的功分别是
怎样计算拉力所做的功?
拉力做功的计算方法
方法
拉力所做的功
其中,k是弹簧的劲度系数,
l是弹簧的伸长量或压缩量
弹性势能的表达式
根据我们刚才的推论,当弹簧处于原长、弹性势能值为0时,这个弹簧被拉长L时弹力做的功就等于弹簧被拉长L时弹簧弹性势能的值,所以有
体会功是能量转化的量度.
一、弹性势能
定义:发生弹性形变的物体各部分之间,由于弹力的相互作用而具有的势能.
二、重力势能的表达式:
弹性势能的表达式:
5.5探究弹性势能的表达式
1.在水平面上竖直放置一轻弹簧,有一物体在它的正上方自由落下,在物体压缩弹簧速度减为零时(
)
A.物体的重力势能最大
B.物体的动能最大
C.弹簧的弹性势能最大
D.物体的弹性势能最小
对弹性势能的理解
对弹性势能的理解
3.
如图所示,劲度系数为k的轻质弹簧一端固定,另一端与物块拴接,物块放在光滑水平面上。现用外力缓慢推动物块,将弹簧压缩了长度l,试用图象法求在此过程中外力所做的功。
4.
两弹簧的劲度系数之比为1:2,在弹性限度内的形变量之比为2:1,则它们的弹性势能之比为(
)
A.
1:2
B.
2:1
C.
1:4
D.
4:1
一物体以初速度v0冲向与竖起墙壁相连的轻质弹簧,墙壁与物体间的弹簧被物体压缩,在此过程中,下列说法正确的是:( )
A、物体对弹簧做的功与弹簧的压缩量成正比
B、物体向墙壁移动相同的距离,弹力做的功不相等
C、弹力做正功,弹簧的弹性势能减小
D、弹力做负功,弹簧的弹性势能增加
BCD
对弹性势能的理解
一竖直弹簧下端固定于水平地面上,小球从弹簧的正上方高为h的地方自由下落到弹簧上端,如图所示,经几次反弹以后小球最终在弹簧上静止于某一点A处,则(
)
A.h愈大,弹簧在A点的压缩量愈大
B.弹簧在A点的压缩量与h无关
C.h愈大,最终小球静止在A点时弹簧的弹性势能愈大
D.小球第一次到达A点时弹簧的弹性势能比最终小球静止在A点时弹簧的弹性势能大
B
对弹性势能的理解
同课章节目录
- 第一章 怎样研究抛体运动
- 1 飞机投弹与平抛运动
- 2 研究平抛运动的规律
- 3 研究斜抛运动
- 第二章 研究圆周运动
- 1 怎样描述圆周运动
- 2 研究匀速圆周运动的规律
- 3 圆周运动的案例分析
- 4 研究离心现象及其应用
- 第三章 动能的变化与机械功
- 1 探究动能变化跟功的关系
- 2 研究功与功率
- 3 动能定理的应用
- 第四章 能量守恒与可持续发展
- 1 势能的变化与机械功
- 2 研究机械能守恒定律
- 3 能量的转化与守恒
- 4 能源与可持续发展
- 第五章 万有引力与航天
- 1 从托勒密到开普勒
- 2 万有引力定律是怎样发现的
- 3 万有引力定律与天文学的新发现
- 4 飞出地球去
- 第六章 经典力学与现代物理
- 1 经典力学的巨大成就和局限性
- 2 狭义相对论的基本原理
- 3 爱因斯坦心目中的宇宙
- 4 微观世界与量子论
