沪教版高中数学高二下册:11.2直线的倾斜角和斜率 教案(Word)
文档属性
| 名称 | 沪教版高中数学高二下册:11.2直线的倾斜角和斜率 教案(Word) |  | |
| 格式 | zip | ||
| 文件大小 | 510.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 12:35:56 | ||
图片预览


文档简介
《直线的倾斜角与斜率》教学设计
一、教材分析
教学内容
本节主要讲直线的倾斜角和斜率,共分二课时。这是第一课时,该节主要学习的内容是直线的倾斜角和斜率的概念以及斜率公式.
教材所处地位及前后的联系
本节是高中解析几何内容的开始,也是解析几何的重要概念之一,该节是学生学习用坐标法研究图形,研究几何问题的初步知识,这些知识是初步渗透解析几何的基本思想和基本研究方法,本课有着开启全章,为进一步学习圆锥曲线方程、导数等知识的基础.
二
、教学目标
1、理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式;
2、通过学习直线的倾斜角和斜率有关的概念,培养学习的数学理解能力;通过对斜率公式的推导,增强学生运用坐标法解决几何问题的能力;
3、学生通过主动探究,合作学习,相互交流,增强学生的数学应用意识,提高学生数学思维的情趣,给学生成功的体验,强化学生参与意识与主体作用.
三、学情分析
作为教学对象的学生是学习主体,为了突出学生的主体的地位,教师须全面研究学生,了解学生.
1、认知结构
经过半年多时间的学习,学生对数学概念及思维方法的认识水平有了较大提高.但不同层次的学生之间仍存在着较大的差距,尤其表现在对知识的探究、联想、迁移能力上.在新课中,运用了生活中的实例,多媒体动画效果,引导学生思维的“上路”,让学生主动参与探究过程.
2、情感结构
随着年龄的增大,阅历的丰富,高中学生自主意识的增强,有独立思考问题、发现问题的能力.在学生的探索活动中,主动通过设疑、质疑、提示等启发示手段,帮助他们分析问题,激发学生的学习的兴趣.
四、教学重难点
重点:直线的倾斜角和斜率的概念,过两点的直线的斜率公式
难点:斜率概念的理解和过两点的直线的斜率公式的推导
五、教学方法
本节课主要是教给学生“动眼看、动手算、动脑想、动口说、勤钻研”的研究式学习方法,这样增加了学生自主参与,合作交流的机会,教给学生获取知识的途径,思考问题的方法,使学生真正成为教学的主体,使学生“学”有所“思”,“思”有新“得”,“练”有所“获”,让学生产生一种成就感,激发学生的兴兴趣.
六、教学条件分析
可以借用电子白板及几何画板动态演示坐标系下确定直线的几何要素,倾斜角的变化与斜率变化之间的关系等.借助实物展台展示学生的研究方法和计算过程.
七、教学过程
(一)引言
在几何问题的研究中,我们常常依据几何图形中点、直线、平面的关系研究几何图形的性质.现在,我们采用另外一种研究方法:坐标法.坐标法是以坐标系为桥梁,把几何问题转化为代数问题,通过代数运算研究几何图形性质的方法.它是解析几何中最基本的研究方法.从今天开始,我们就来学习解析几何的内容.
(设计意图:使学生了解学习的新内容的特点及意义)?
(二)倾斜角概念的形成
我们知道,在平面直角坐标系内两点确定一条直线,一点能确定一条直线的位置吗?(不能)过一点有多少条直线?(无数条).
(倾斜程度不同)
【师】这些直线区别在哪里呢?
【生】倾斜程度不同
【师】这节课我们来研究直线的倾斜角与斜率
(设计意图:自然合理地提出问题,从最简单问题着手,创造轻松的氛围。
学生直观感受到,确定直线的两个要素,从而引出了直线的倾斜角和刻画倾斜程度的量—斜率)
【板书】直线的倾斜角和斜率
来看本课【学习目标】
1.理解倾斜角的概念.
2.理解斜率的定义和斜率公式.
3.掌握过两点的直线斜率的计算方法,并能用于计算.
本节课要解决这三个问题:
(1)什么是直线的倾斜角,它是怎样定义的?
(2)什么是直线的斜率,它的公式是什么?直线的倾斜角和斜率之间有何联系?
(3)已知直线上两点坐标,怎样求出这条直线的斜率?
【师】请同学们将书打开第82页,阅读教材第82页至第83页“思考”,完成学案上的问题1~问题4.
(设计意图:通过学生自学,掌握基本内容。体现出“学生自己给自己上新课”)
【探究一】直线的倾斜角与斜率
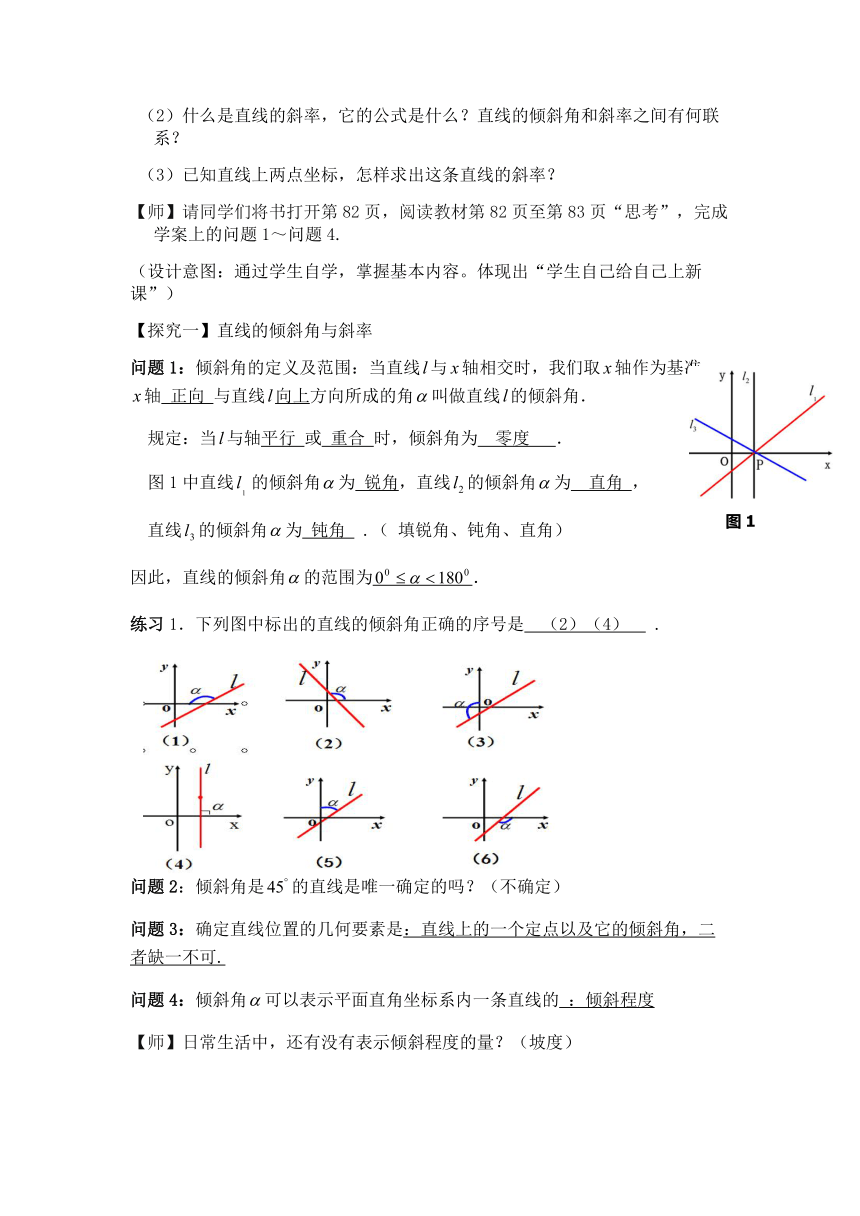
问题1:倾斜角的定义及范围:当直线与轴相交时,我们取轴作为基准,
(
图
1
)轴
正向
与直线向上方向所成的角叫做直线的倾斜角.
规定:当与轴平行
或
重合
时,倾斜角为
零度
.
图1中直线的倾斜角为
锐角,直线的倾斜角为
直角
,
直线的倾斜角为
钝角
.(
填锐角、钝角、直角)
因此,直线的倾斜角的范围为.
练习1.下列图中标出的直线的倾斜角正确的序号是
(2)(4)
.
问题2:倾斜角是的直线是唯一确定的吗?(不确定)
问题3:确定直线位置的几何要素是:直线上的一个定点以及它的倾斜角,二者缺一不可.
问题4:倾斜角可以表示平面直角坐标系内一条直线的
:倾斜程度
【师】日常生活中,还有没有表示倾斜程度的量?(坡度)
展示日常生活中一些坡度的图片,以楼梯为例,展示图片,说明:
【师】
这两幅楼梯哪个坡度更大呢?(第二个)怎样用数学语言描述“坡度更大”这个意思呢?
学生思考讨论,回答.
【生】
,当前进量一样的情况下,升高量越大,坡度就越大,也就是楼梯倾斜角的正切值越大.
问题5:直线斜率的定义:我们把一条直线的倾斜角的
正切
值叫做这条直线的斜率.即
.
练习2.已知直线的倾斜角,请求对应的斜率.
(1);
(2);
(3);
(4);
倾斜角的范围
直线斜率的范围
K不存在
问题6:图2是的图象,你能根据图2由直线倾斜角的范围得出斜率的取值范围吗?请填入下表.
(设计意图:通过学生回答,教师了解学生对斜率的掌握情况及对斜率部分解释)
【探究二】已知直线上两点坐标求直线的斜率
问题7:已知直线经过点,结合图(1)和
图(2),说出斜率公式的推导过程.
【思考】当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?
【生】适用,当直线与轴平行或重合时,.
【思考】当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
【生】不适用,当直线与轴平行或重合时,不存在
(设计意图:让学生上黑板演板斜率的推导过程,掌握学生自学情况和教师对斜率的推导加以解释)
问题8:已知直线上两点,运用上述公式计算直线
的斜率时,与的顺序有关吗?
你能结合问题7中的图(3)图(4)说出为什么吗?
【生】没有关系,.
三、例题讲解
例1、如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
【当堂训练】
1、请求出经过下列两点直线的斜率:
(1)
(2)
(3)
(4)
2、判断下列命题的真假:
(1)任意一条直线都有倾斜角和斜率.
(
)
(2)两直线倾斜角相等,则斜率相等.
(
)
(3)两直线斜率相等,则倾斜角也相等.
(
)
(4)直线的倾斜角越大,它的斜率也越大.(
)
3、已知直线过点A(2,)、B(1,
),求它的斜率和倾斜角.
(设计意图:学生当堂训练,加深对本节课知识的了解。教师也可以了解学生的掌握情况)
四、本课小结
1、我掌握了……
2、我还不清楚的是……
3、我自己的表现:A.
很棒、B.
满意、C.加油
五、作业
课本89页习题A组的1~4题.
一、教材分析
教学内容
本节主要讲直线的倾斜角和斜率,共分二课时。这是第一课时,该节主要学习的内容是直线的倾斜角和斜率的概念以及斜率公式.
教材所处地位及前后的联系
本节是高中解析几何内容的开始,也是解析几何的重要概念之一,该节是学生学习用坐标法研究图形,研究几何问题的初步知识,这些知识是初步渗透解析几何的基本思想和基本研究方法,本课有着开启全章,为进一步学习圆锥曲线方程、导数等知识的基础.
二
、教学目标
1、理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式;
2、通过学习直线的倾斜角和斜率有关的概念,培养学习的数学理解能力;通过对斜率公式的推导,增强学生运用坐标法解决几何问题的能力;
3、学生通过主动探究,合作学习,相互交流,增强学生的数学应用意识,提高学生数学思维的情趣,给学生成功的体验,强化学生参与意识与主体作用.
三、学情分析
作为教学对象的学生是学习主体,为了突出学生的主体的地位,教师须全面研究学生,了解学生.
1、认知结构
经过半年多时间的学习,学生对数学概念及思维方法的认识水平有了较大提高.但不同层次的学生之间仍存在着较大的差距,尤其表现在对知识的探究、联想、迁移能力上.在新课中,运用了生活中的实例,多媒体动画效果,引导学生思维的“上路”,让学生主动参与探究过程.
2、情感结构
随着年龄的增大,阅历的丰富,高中学生自主意识的增强,有独立思考问题、发现问题的能力.在学生的探索活动中,主动通过设疑、质疑、提示等启发示手段,帮助他们分析问题,激发学生的学习的兴趣.
四、教学重难点
重点:直线的倾斜角和斜率的概念,过两点的直线的斜率公式
难点:斜率概念的理解和过两点的直线的斜率公式的推导
五、教学方法
本节课主要是教给学生“动眼看、动手算、动脑想、动口说、勤钻研”的研究式学习方法,这样增加了学生自主参与,合作交流的机会,教给学生获取知识的途径,思考问题的方法,使学生真正成为教学的主体,使学生“学”有所“思”,“思”有新“得”,“练”有所“获”,让学生产生一种成就感,激发学生的兴兴趣.
六、教学条件分析
可以借用电子白板及几何画板动态演示坐标系下确定直线的几何要素,倾斜角的变化与斜率变化之间的关系等.借助实物展台展示学生的研究方法和计算过程.
七、教学过程
(一)引言
在几何问题的研究中,我们常常依据几何图形中点、直线、平面的关系研究几何图形的性质.现在,我们采用另外一种研究方法:坐标法.坐标法是以坐标系为桥梁,把几何问题转化为代数问题,通过代数运算研究几何图形性质的方法.它是解析几何中最基本的研究方法.从今天开始,我们就来学习解析几何的内容.
(设计意图:使学生了解学习的新内容的特点及意义)?
(二)倾斜角概念的形成
我们知道,在平面直角坐标系内两点确定一条直线,一点能确定一条直线的位置吗?(不能)过一点有多少条直线?(无数条).
(倾斜程度不同)
【师】这些直线区别在哪里呢?
【生】倾斜程度不同
【师】这节课我们来研究直线的倾斜角与斜率
(设计意图:自然合理地提出问题,从最简单问题着手,创造轻松的氛围。
学生直观感受到,确定直线的两个要素,从而引出了直线的倾斜角和刻画倾斜程度的量—斜率)
【板书】直线的倾斜角和斜率
来看本课【学习目标】
1.理解倾斜角的概念.
2.理解斜率的定义和斜率公式.
3.掌握过两点的直线斜率的计算方法,并能用于计算.
本节课要解决这三个问题:
(1)什么是直线的倾斜角,它是怎样定义的?
(2)什么是直线的斜率,它的公式是什么?直线的倾斜角和斜率之间有何联系?
(3)已知直线上两点坐标,怎样求出这条直线的斜率?
【师】请同学们将书打开第82页,阅读教材第82页至第83页“思考”,完成学案上的问题1~问题4.
(设计意图:通过学生自学,掌握基本内容。体现出“学生自己给自己上新课”)
【探究一】直线的倾斜角与斜率
问题1:倾斜角的定义及范围:当直线与轴相交时,我们取轴作为基准,
(
图
1
)轴
正向
与直线向上方向所成的角叫做直线的倾斜角.
规定:当与轴平行
或
重合
时,倾斜角为
零度
.
图1中直线的倾斜角为
锐角,直线的倾斜角为
直角
,
直线的倾斜角为
钝角
.(
填锐角、钝角、直角)
因此,直线的倾斜角的范围为.
练习1.下列图中标出的直线的倾斜角正确的序号是
(2)(4)
.
问题2:倾斜角是的直线是唯一确定的吗?(不确定)
问题3:确定直线位置的几何要素是:直线上的一个定点以及它的倾斜角,二者缺一不可.
问题4:倾斜角可以表示平面直角坐标系内一条直线的
:倾斜程度
【师】日常生活中,还有没有表示倾斜程度的量?(坡度)
展示日常生活中一些坡度的图片,以楼梯为例,展示图片,说明:
【师】
这两幅楼梯哪个坡度更大呢?(第二个)怎样用数学语言描述“坡度更大”这个意思呢?
学生思考讨论,回答.
【生】
,当前进量一样的情况下,升高量越大,坡度就越大,也就是楼梯倾斜角的正切值越大.
问题5:直线斜率的定义:我们把一条直线的倾斜角的
正切
值叫做这条直线的斜率.即
.
练习2.已知直线的倾斜角,请求对应的斜率.
(1);
(2);
(3);
(4);
倾斜角的范围
直线斜率的范围
K不存在
问题6:图2是的图象,你能根据图2由直线倾斜角的范围得出斜率的取值范围吗?请填入下表.
(设计意图:通过学生回答,教师了解学生对斜率的掌握情况及对斜率部分解释)
【探究二】已知直线上两点坐标求直线的斜率
问题7:已知直线经过点,结合图(1)和
图(2),说出斜率公式的推导过程.
【思考】当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?
【生】适用,当直线与轴平行或重合时,.
【思考】当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
【生】不适用,当直线与轴平行或重合时,不存在
(设计意图:让学生上黑板演板斜率的推导过程,掌握学生自学情况和教师对斜率的推导加以解释)
问题8:已知直线上两点,运用上述公式计算直线
的斜率时,与的顺序有关吗?
你能结合问题7中的图(3)图(4)说出为什么吗?
【生】没有关系,.
三、例题讲解
例1、如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
【当堂训练】
1、请求出经过下列两点直线的斜率:
(1)
(2)
(3)
(4)
2、判断下列命题的真假:
(1)任意一条直线都有倾斜角和斜率.
(
)
(2)两直线倾斜角相等,则斜率相等.
(
)
(3)两直线斜率相等,则倾斜角也相等.
(
)
(4)直线的倾斜角越大,它的斜率也越大.(
)
3、已知直线过点A(2,)、B(1,
),求它的斜率和倾斜角.
(设计意图:学生当堂训练,加深对本节课知识的了解。教师也可以了解学生的掌握情况)
四、本课小结
1、我掌握了……
2、我还不清楚的是……
3、我自己的表现:A.
很棒、B.
满意、C.加油
五、作业
课本89页习题A组的1~4题.
