沪教版高中数学高二下册:11.3 两条直线的位置关系-两条直线的夹角 课件(共13张PPT)
文档属性
| 名称 | 沪教版高中数学高二下册:11.3 两条直线的位置关系-两条直线的夹角 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 660.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
11.3
两条直线的夹角
我们已经学习了两直线的位置关系有平行、重合和相交。当两条直线相交时,用什么“量”来描述两条直线的相对位置关系呢?
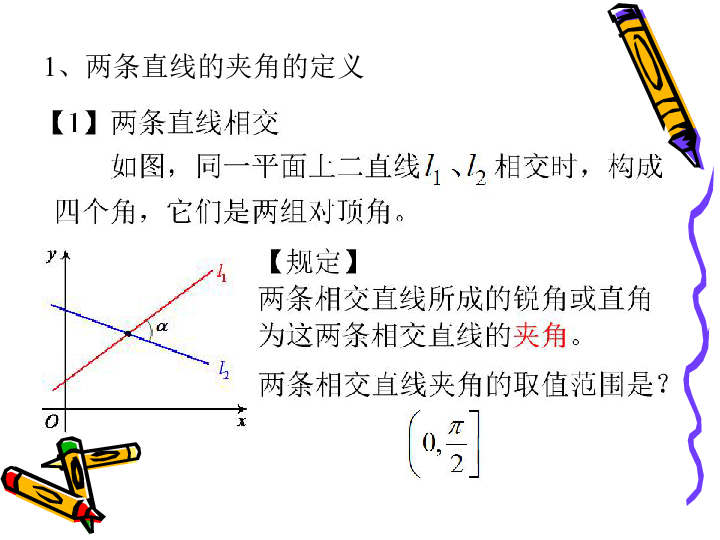
1、两条直线的夹角的定义
2、求两条直线的夹角
系数确定直线的方程,方程确定直线及其位置,所以可以利用方程系数来计算夹角。
例1
例2
例3
本节课学习了哪些内容?
如图,同一平面上二直线41、2相交时,构成
四个角,它们是两组对顶角
【规定】
两条相交直线所成的锐角或直角
为这两条相交直线的夹角。
两条相交直线夹角的取值范围是?
【2】两条直线平行或重合
若两条直线平行或重合,则规定其夹角为0(或0°)。
问题
1、两直线的夹角取值范围是?
2、若两直线的夹角为一,两直线的位置关系是?
3、若两直线的夹角为0,两直线的位置关系是?
已知直线h1:a1x+by+C1=0,
1:a2x+b,y+c2=0夹角为a。
如何利用方程系数来计算夹角?
设d1与a2的夹角为6
h1、l2的夹角a与它们方向向量的夹角是否相等?
y
=日
a=x-6
e∈[0.7
O,若O∈[0,
丌-,若O∈(,m
2
如何利用1、l2方向向量的夹角来求
它们的夹角a?
cos
a=cos
61
ld1|·|d
1a2+b1b2
cosC=
attb
+:
利用夹角余弦值能求出夹角吗?
公式(
)是通过对直线4、l2的方向向量的讨论
得到的,法向量也是能描述直线方向的量,两直
线法向量的夹角余弦值是多少?与两直线夹角
余弦值有什么关系?
已知二直线的方程分别为4:3x-y+2=0
l2:5x+2y-3=0。求1与l2的夹角。
已知直线l经过点P(-2,√3),且与lo:
x-√3y+2=0的夹角为,求直线/的方程。
3
已知两直线的方程分别为1:x+(m+1)y+m-2=0
mx+2y+8=0。当m为何值时,4与12垂直。
小结
11.3
两条直线的夹角
我们已经学习了两直线的位置关系有平行、重合和相交。当两条直线相交时,用什么“量”来描述两条直线的相对位置关系呢?
1、两条直线的夹角的定义
2、求两条直线的夹角
系数确定直线的方程,方程确定直线及其位置,所以可以利用方程系数来计算夹角。
例1
例2
例3
本节课学习了哪些内容?
如图,同一平面上二直线41、2相交时,构成
四个角,它们是两组对顶角
【规定】
两条相交直线所成的锐角或直角
为这两条相交直线的夹角。
两条相交直线夹角的取值范围是?
【2】两条直线平行或重合
若两条直线平行或重合,则规定其夹角为0(或0°)。
问题
1、两直线的夹角取值范围是?
2、若两直线的夹角为一,两直线的位置关系是?
3、若两直线的夹角为0,两直线的位置关系是?
已知直线h1:a1x+by+C1=0,
1:a2x+b,y+c2=0夹角为a。
如何利用方程系数来计算夹角?
设d1与a2的夹角为6
h1、l2的夹角a与它们方向向量的夹角是否相等?
y
=日
a=x-6
e∈[0.7
O,若O∈[0,
丌-,若O∈(,m
2
如何利用1、l2方向向量的夹角来求
它们的夹角a?
cos
a=cos
61
ld1|·|d
1a2+b1b2
cosC=
attb
+:
利用夹角余弦值能求出夹角吗?
公式(
)是通过对直线4、l2的方向向量的讨论
得到的,法向量也是能描述直线方向的量,两直
线法向量的夹角余弦值是多少?与两直线夹角
余弦值有什么关系?
已知二直线的方程分别为4:3x-y+2=0
l2:5x+2y-3=0。求1与l2的夹角。
已知直线l经过点P(-2,√3),且与lo:
x-√3y+2=0的夹角为,求直线/的方程。
3
已知两直线的方程分别为1:x+(m+1)y+m-2=0
mx+2y+8=0。当m为何值时,4与12垂直。
小结
