沪教版高中数学高二下册12.1 曲线和方程 课件(共20张PPT)
文档属性
| 名称 | 沪教版高中数学高二下册12.1 曲线和方程 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 12:31:49 | ||
图片预览



文档简介
(共20张PPT)
12.1
曲线与方程
2012年6月16日18时37分神舟九号飞船发射升空,神舟九号与目标飞行器天宫一号成功对接,这是中国实施的首次载人空间交会对接,并于2012年6月29日10点00分安全返回。掀开了中国航天史上极具突破性的一章。
科学家们是如何准确地给出飞船的运行轨道?
情景引入
曲线是由质点按某种规律运动形成的
情景引入
要研究曲线我们要先确定质点的位置
问题1:我们怎么确定一个质点在平面内的位置?
利用平面直角坐标系确定质点的坐标(x,y)
问题2:请同学们在平面直角坐标系中画出一条直线
能否用所学过的数学知识来表示这条直线?
直线方程
方程(英文:equation)是表示两个数学式(如两个数、函数、量、运算)之间相等关系的一种等式
情景引入
曲线与方程
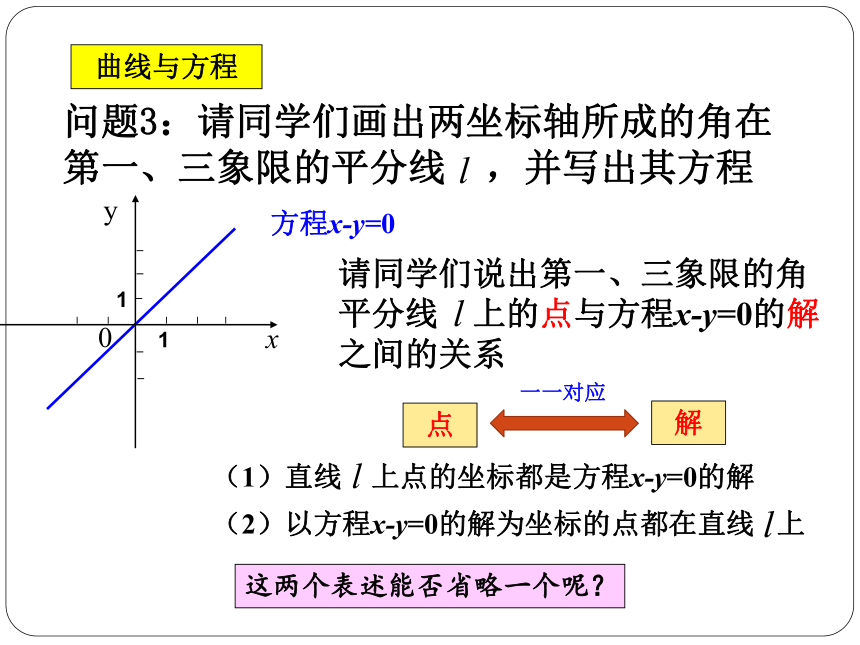
方程x-y=0
这两个表述能否省略一个呢?
点
解
一一对应
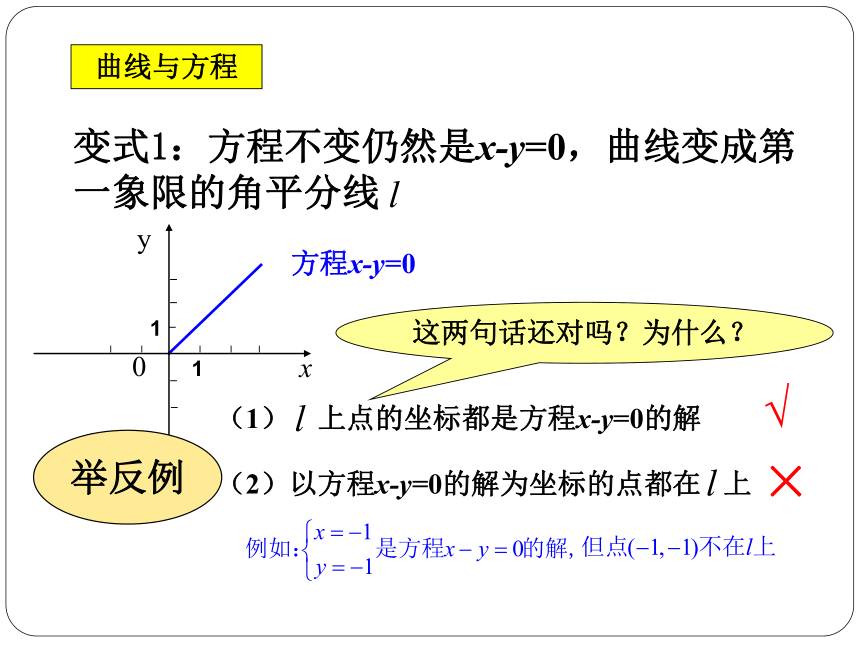
这两句话还对吗?为什么?
√
×
曲线与方程
方程x-y=0
举反例
方程x-y=0(x≥0)
变式2:曲线不变仍然是第一、三象限的角平分线,方程变为x-y=0(x≥0)
这两句话对吗?为什么?
√
×
曲线与方程
曲线与方程
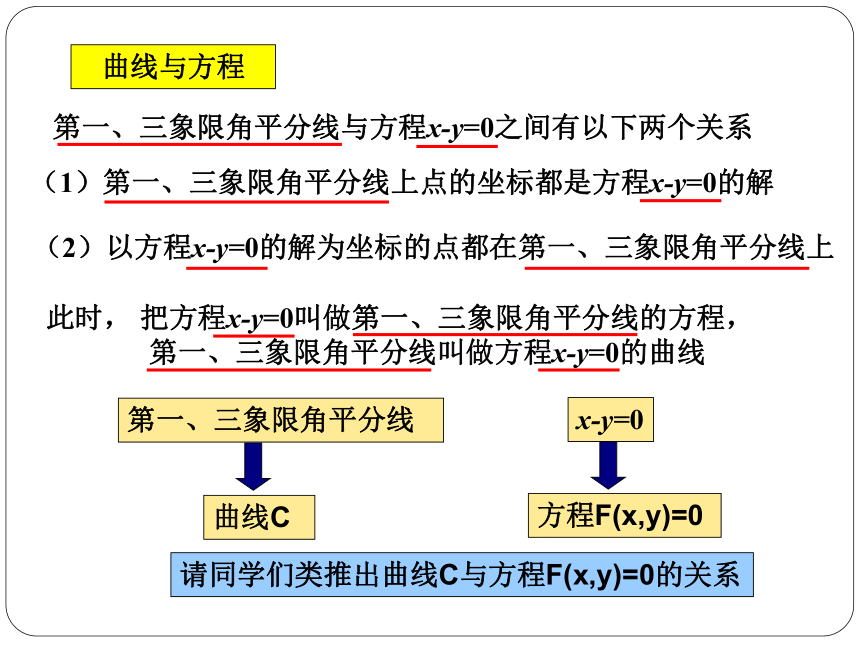
此时,
把方程x-y=0叫做第一、三象限角平分线的方程,
第一、三象限角平分线叫做方程x-y=0的曲线
(1)第一、三象限角平分线上点的坐标都是方程x-y=0的解
(2)以方程x-y=0的解为坐标的点都在第一、三象限角平分线上
第一、三象限角平分线
x-y=0
曲线C
方程F(x,y)=0
第一、三象限角平分线与方程x-y=0之间有以下两个关系
请同学们类推出曲线C与方程F(x,y)=0的关系
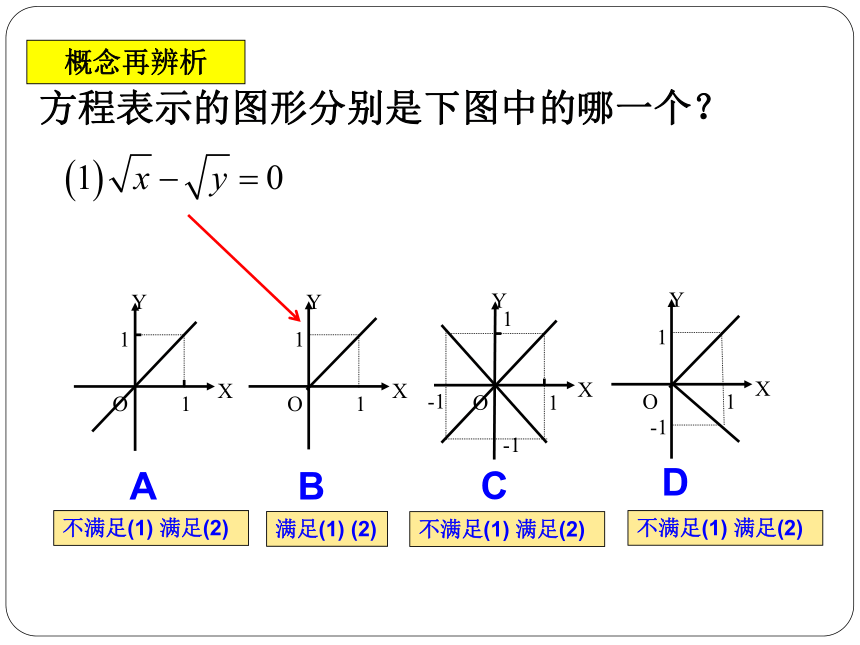
方程表示的图形分别是下图中的哪一个?
A
B
C
D
概念再辨析
不满足(1)
满足(2)
满足(1)
(2)
不满足(1)
满足(2)
不满足(1)
满足(2)
方程表示的图形分别是下图中的哪一个?
A
B
C
D
概念再辨析
满足(1)不满足(2)
满足(1)不满足(2)
满足(1)
(2)
满足(1)不满足(2)
方程表示的图形分别是下图中的哪一个?
A
B
C
D
概念再辨析
(1)
(2)都不满足
满足(1)不满足(2)
不满足(1)
满足(2)
满足(1)
(2)
方程表示的图形分别是下图中的哪一个?
A
B
C
D
概念再辨析
概念再辨析
这两个表述都成立
这两个表述都不成立
典型例题
例1、已知两点A(-1,1)和B(3,-1),求证:线段AB的垂直平分线
的方程是2x-y-2=0
M1
分析:(1)证明曲线C上的点的坐标都是方程F(x,y)=0的解
定义证明
1、线段垂直平分线上的点到线段两端距离相等
2、到线段两端距离相等的点在线段垂直平分线上
典型例题
例1、已知两点A(-1,1)和B(3,-1),求证:线段AB的垂直平分线
的方程是2x-y-2=0
(2)证明以方程F(x,y)=0的解为坐标的点都是曲线C上的点
2、到线段两端距离相等的点在线段垂直平分线上
1、线段垂直平分线上的点到线段两端距离相等
分析:(1)证明曲线C上的点的坐标都是方程F(x,y)=0的解
请同学们大胆猜想神舟九号飞船的飞行轨道是如何确定的?飞行轨道大致是什么曲线?
生活中的应用
生活中的应用
请同学们四人一小组讨论,生活中还有哪些领域涉及到了今天所学的知识?
小结
请同学们小结一下今天所学的知识
借助于平面坐标系用代数方法研究平面上图形性质的学科称为平面解析几何
曲线
方程
坐标系
几何“形”
代数“数”
数形结合
课后作业
1、练习册P18,1-3
书P33练习12.1(1)
2、请同学们自行选定一个生活中的参照物建立坐标系,画出你上学的路径,看看能否用方程表示
12.1
曲线与方程
2012年6月16日18时37分神舟九号飞船发射升空,神舟九号与目标飞行器天宫一号成功对接,这是中国实施的首次载人空间交会对接,并于2012年6月29日10点00分安全返回。掀开了中国航天史上极具突破性的一章。
科学家们是如何准确地给出飞船的运行轨道?
情景引入
曲线是由质点按某种规律运动形成的
情景引入
要研究曲线我们要先确定质点的位置
问题1:我们怎么确定一个质点在平面内的位置?
利用平面直角坐标系确定质点的坐标(x,y)
问题2:请同学们在平面直角坐标系中画出一条直线
能否用所学过的数学知识来表示这条直线?
直线方程
方程(英文:equation)是表示两个数学式(如两个数、函数、量、运算)之间相等关系的一种等式
情景引入
曲线与方程
方程x-y=0
这两个表述能否省略一个呢?
点
解
一一对应
这两句话还对吗?为什么?
√
×
曲线与方程
方程x-y=0
举反例
方程x-y=0(x≥0)
变式2:曲线不变仍然是第一、三象限的角平分线,方程变为x-y=0(x≥0)
这两句话对吗?为什么?
√
×
曲线与方程
曲线与方程
此时,
把方程x-y=0叫做第一、三象限角平分线的方程,
第一、三象限角平分线叫做方程x-y=0的曲线
(1)第一、三象限角平分线上点的坐标都是方程x-y=0的解
(2)以方程x-y=0的解为坐标的点都在第一、三象限角平分线上
第一、三象限角平分线
x-y=0
曲线C
方程F(x,y)=0
第一、三象限角平分线与方程x-y=0之间有以下两个关系
请同学们类推出曲线C与方程F(x,y)=0的关系
方程表示的图形分别是下图中的哪一个?
A
B
C
D
概念再辨析
不满足(1)
满足(2)
满足(1)
(2)
不满足(1)
满足(2)
不满足(1)
满足(2)
方程表示的图形分别是下图中的哪一个?
A
B
C
D
概念再辨析
满足(1)不满足(2)
满足(1)不满足(2)
满足(1)
(2)
满足(1)不满足(2)
方程表示的图形分别是下图中的哪一个?
A
B
C
D
概念再辨析
(1)
(2)都不满足
满足(1)不满足(2)
不满足(1)
满足(2)
满足(1)
(2)
方程表示的图形分别是下图中的哪一个?
A
B
C
D
概念再辨析
概念再辨析
这两个表述都成立
这两个表述都不成立
典型例题
例1、已知两点A(-1,1)和B(3,-1),求证:线段AB的垂直平分线
的方程是2x-y-2=0
M1
分析:(1)证明曲线C上的点的坐标都是方程F(x,y)=0的解
定义证明
1、线段垂直平分线上的点到线段两端距离相等
2、到线段两端距离相等的点在线段垂直平分线上
典型例题
例1、已知两点A(-1,1)和B(3,-1),求证:线段AB的垂直平分线
的方程是2x-y-2=0
(2)证明以方程F(x,y)=0的解为坐标的点都是曲线C上的点
2、到线段两端距离相等的点在线段垂直平分线上
1、线段垂直平分线上的点到线段两端距离相等
分析:(1)证明曲线C上的点的坐标都是方程F(x,y)=0的解
请同学们大胆猜想神舟九号飞船的飞行轨道是如何确定的?飞行轨道大致是什么曲线?
生活中的应用
生活中的应用
请同学们四人一小组讨论,生活中还有哪些领域涉及到了今天所学的知识?
小结
请同学们小结一下今天所学的知识
借助于平面坐标系用代数方法研究平面上图形性质的学科称为平面解析几何
曲线
方程
坐标系
几何“形”
代数“数”
数形结合
课后作业
1、练习册P18,1-3
书P33练习12.1(1)
2、请同学们自行选定一个生活中的参照物建立坐标系,画出你上学的路径,看看能否用方程表示
