人教A版 必修三 第二单元 统计 统计单元复习与巩固学案(无答案)
文档属性
| 名称 | 人教A版 必修三 第二单元 统计 统计单元复习与巩固学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 14:40:23 | ||
图片预览




文档简介
统计单元复习与巩固
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
?
熟悉三种抽样方法(简单随机抽样、系统抽样、分层抽样)的特点、适用范围、实施步骤,能熟练应用三种抽样方法进行抽样.
?
熟悉数据的收集、整理、分析过程,会列频率分布表,会画频率分布直方图、折线图、茎叶图等,并能从统计图中提取有用信息,解决一些问题.
?
熟悉平均数、众数、中位数、极差、方差、标准差等各数字特征的意义,熟练掌握这些数字特征的计算或提取方法,并会由样本的数字特征对总体进行科学合理的估计,以解决一些实际问题.
?
能认识变量间的相关关系,利用散点图的直观性,进一步认识线性相关关系,了解最小二乘法思想,能由公式求回归直线方程.
重点难点:
?
重点:三种抽样方法及其应用;利用频率分布表和统计图表做统计分析;理解平均数、方差、标准差等数字特征的意义,利用样本的数字特征对总体进行合理估计,得出结论.
?
难点:抽样方法的选取和怎样用样本估计总体及对最小二乘法思想的理解.
学习策略:
本章统计部分虽然在内容与要求上比初中“统计初步”略有提高,但总的来看仍属于统计中的一些较为初步的知识.
?
注意理论联系实际,培养用数学的意识.
学数学的出发点和归宿是用数学,联系实际是本章的一个显著特点.这一章大量引入各类实际问题,要能以数学的眼光来观察所处的客观世界,逐渐养成借助助数学的思想、观点、方法来思考研究问题,解决问题,培养用数学的意识.
?
要求学会用科学计算器处理统计计算.
统计是与数据打交道的,处理问题时常计算量大而且比较复杂,如果不用科学计算器将会寸步难行.
二、学习与应用
知识点一:随机抽样
简单随机抽样、系统抽样和分层抽样的共同特点是在抽样过程中每一个个体被抽取的概率
,体现了这些抽样方法的客观性和公平性.一般地,当总体中的个体数较少时,常采用
;当总体中的个体数较多时,常采用
;当已知总体由差异明显的几部分组成时,常采用
.当然,采用抽样方法解决实际问题时,三种抽样方法经常交叉起来使用.
要点诠释:
应用抽样方法时要注意以下几点:
(1)用随机数表法抽样时,对个体所编的号码位数要
.当问题所给位数不等时,以位数较多的为准,在位数较少的数前面添“0”,凑齐位数.
(2)用系统抽样法抽样时,如果总体容量N能被样本容量n整除,抽样间隔为k=
;如果总体容量N不能被样本容量n整除,先用简单随机抽样剔除多余个体,抽样间隔k=
.
(3)用分层抽样法抽样时,分成的各层标准要
,互不
;各层
抽取的比例都
样本容量在总体中的比例,即.
知识点二:用样本估计总体
(一)用样本的频率分布估计总体分布
总体分布是指总体取值的分布规律,这种分布一般是不知晓的.我们往往用样本的频率分布去估计总体分布.一般地,样本容量越
,估计越精确,用样本频率分布去估计总体分布的基本步骤是:
(1)从总体中抽取合适的样本;
(2)分组统计样本数据;
(3)计算各组的频率,作频率分布表;
(4)画频率分布直方图.
频率分布表能使我们清楚地知道数据分布在各个小组的
,而频率分布直方图则是从各个小组数据在样本容量所占比例大小的角度来表示数据分布的规律.把频率分布直方图各个矩形的上端的中点用线段连接起来,就得到频率分布折线图.这样,通过样本频率分布就可以大致估计出总体的分布.要特别指出的是:频率分布直方图中,矩形面积=
.
在样本数据较少时,也常用茎叶图表示数据.茎叶图刻画数据有两个优点:一是所有的信息都可以从图中得到;二是茎叶图便于记录和表示.但当数据位数较多时,使用茎叶图就不够方便了.
(二)用样本的数字特征估计总体的数字特征
(1)众数、中位数和平均数都是描述数据的“
”的数字特征.它们各有优缺点,要深刻理解和把握它们在反映样本数据上的特点,结合实际情况,灵活选用.
(2)方差和标准差都是用来描述一组数据
的特征数,常用来比较两组数据的波动大小.方差较大的波动较
,方差较小的波动较
.
要点诠释:
用样本估计总体,是研究统计问题的一个基本思想方法,样本容量越
,估计越精确.
(1)当总体中的个体取不同值很少时,其频率分布表由所取的样本的不同值及相应的频率来表示,其几何表示就是相应的条形图;
(2)当总体中的个体取不同值较多时,对其频率分布的研究要用到整理样本数据的知识,列出频率分布表和区间内取值的频率分布表和频率分布直方图;
(3)当样本容量无限增大,频率分布直方图趋近于总体密度曲线.
知识点三:回归分析
(一)两个变量线性相关关系的判断
判断解释变量x与预报变量y是否具有线性相关关系,一种常见的简便可行的方法就是作出
图,从点的分布特征来判定是否线性相关:如果这些点大致分布在通过散点图中心的一条
附近,那么就说这两个变量之间具有线性相关关系,这条直线叫做回归直线.
(二)线性回归分析的方法、步骤
利用回归分析的方法对具有线性相关关系的变量进行研究的步骤为:
(1)画出两个变量的
图;
(2)求
方程;
(3)用
方程进行预报.
要点诠释:
(1)应该注意回归直线是指各样本点与此直线在整体上是最贴近的那一条直线,它只能有
条,且过样本点的中心
;
(2)其中求回归直线的方程是关键.而求回归直线的最好方法是“
法”,即对于线性回归模型y=bx+a来说,估计模型中的未知参数和的最好方法就是用最小二乘法估计和,其计算公式为,
.
类型一:抽样方法
例1.一批产品,有一级品100个,二级品60个,三级品40个,分别用系统抽样和分层抽样方法,从这批产品中抽取一容量为20的样本.
思路点拨:系统抽样适用于总体中的个体较多的情况,分层抽样适用于总体由差异明显的几部分组成的情况.
解析:
总结升华:
当总体中的个体较少时,一般可用
;
当总体中的个体较多时,一般可用
;当总体由差异明显的几部分组成时,一般可用
.而简单随机抽样作为一种最简单的抽样方法,又在其中处于一种非常重要的地位.实施简单随机抽样,主要有两种方法:
和
.
举一反三:
【变式1】把容量为100的某个样本数据分为10组,并填写频率分布表,若前七组的累积频率为0.79,而剩下三组的频数成公比大于2的整数等比数列,求剩下三组中频数最高的一组的频数?
答案:
类型二:利用频率分布表和统计图表估计总体
例2.有1个容量为100的样本,数据的分组及各组的频数如下:
;
;
;
;
;
;
.
(1)列出样本的频率分布表(含累积频率);
(2)画出频率分布直方图和累积频率分布图;
(3)根据累积频率分布估计,小于30的数据约占多大百分比.
思路点拨:按照画频率分布直方图的步骤操作,用样本的频率分布估计总体的比例.
解析:
总结升华:
举一反三:
【变式1】对某电子元件进行寿命追踪调查,情况如下:
寿命(h)
100—200
200—300
300—400
400—500
500—600
个
数
20
30
80
40
30
(1)列出频率分布表;
(2)画出频率分布直方图和累积频率分布图;
(3)估计电子元件寿命在100—400h以内的所占的百分比;
(4)估计电子元件寿命在400h以上的所占的百分比.
剖析:通过本题可掌握总体分布估计的各种方法和步骤.
答案:
类型三:用样本的数字特征估计总体
例3.从甲、乙两名运动员中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
甲:7 8 6 8 6 5 9 10 7 4
乙:9 5 7 8 7 6 8 6
7 7
(1)计算甲、乙两人射击命中环数的平均数和标准差;
(2)比较两人的成绩,然后决定选择哪一人参加比赛.
思路点拨:本题只要运用公式求出平均数和标准差即可,平均数大的水平较高.若平均数相同,标准差小的水平较稳定.
解析:
总结升华:
(1)平均数反映数据取值的
水平,平均数越大,平均水平越
.
(2)方差、标准差反映数据的
,方差、标准差越小,表示数据越
.
此类题目只要根据平均数和标准差的公式及其解答步骤求解即可.注意方差与标准差的公式区别与联系.
方差公式为
,
标准差公式为
.
举一反三:
【变式1】某班40人随机分为两组,第一组18人,第二组22人,两组学生在某次数学检测中的成绩如下表:
分
组
平均成绩
标准差
第一组
90
6
第二组
80
4
求全班的平均成绩和标准差.
思路点拨:代入方差公式s2=[(x12+x22+…+xn2)-n]即可求得.
解:
【变式2】甲、乙两人在相同的条件下,射击10次,命中环数如下:
甲:8,6,9,5,10,7,4,8,9,5;
乙:7,6,5,8,6,9,6,8,7,7.
根据以上数据估计两人的技术稳定性,结论是(
)
A.甲优于乙 B.乙优于甲 C.两人没区别 D.两人区别不大
答案:
类型四:线性回归分析
例4.下面是我国居民生活污水排放量的一组数据:
年份
1995
1996
1997
1998
1999
2000
2001
2002
排放量
151
189.1
194.8
203.8
220.9
227.7
232.3
试估计1996年我国居民生活污染排放量,并预测2004年生活污水排放量(单位:).
思路点拨:要估计或预测,可考虑先求回归直线方程.将年份与污水排放量的相关关系表达出来,可先剔除1996年,样本容量为7.
解析:
总结升华:
.
举一反三:
【变式1】某个服装店经营某种服装,在某周内获纯利(元)与该周每天销售这些服装件数之间有如下一组数据:
3
4
5
6
7
8
9
66
69
73
81
89
90
91
已知,.
(1)求,;
(2)求纯利与每天销售件数之间的回归直线方程.
解:
三、总结与测评
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力。
(一)根据简单随机抽样、系统抽样、分层抽样这三种方法的共同点、适用范围和各自特点,恰当选择抽样方法从总体中抽取样本,在选取样本时,要按照各种抽样方法的步骤抽取个体.三种抽样方法的比较如下表:
三种抽样方法比较
类别
共同点
相互联系
适用范围
各自特点
简单随机抽样
(1)抽样过程中每个个体被抽到的机会
(2)抽样过程都是
的抽样
总体中的个数较
从总体中
抽取
系统抽样
在起始部分抽样时采用简单随机抽样
总体中的个数较
将总体均分成几部分,按事先确定的规则在各部分抽取
分层抽样
每层抽样时采用简单随机抽样或系统抽样
总体由
的几部分组成
将总体分成几层,按一定的比例进行抽取
(二)用样本估计总体一般分成两种:一种是用样本的频率分布估计总体的分布;另一种是用样本的数字特征(如平均数、标准差等)估计总体的数字特征.
所谓第一种就是利用样本的频率分布表和频率分布直方图对总体情况作出估计,有时也利用频率分布折线图和茎叶图对总体估计.直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到在分布表中看不清楚的数据模式,这样根据样本的频率分布,我们可以大致估计出总体的分布.但是,当总体的个体数较多时,所需抽样的样本容量也不能太小,随着样本容量的增加,频率分布折线图会越来越接近于一条光滑曲线,统计中称这条曲线为总体密度曲线,它能给我们提供更加精细的信息.在样本数据较少时,用茎叶图表示数据的效果较好,它不但可以保留所有信息,而且可以随时记录,这对数据的记录和表示都能带来方便.
所谓第二种就是为了从整体上更好地把握总体的规律,我们还可以通过样本数据的众数、中位数、平均数和标准差等数字特征对总体的数字特征作出估计.众数就是样本数据中出现最多的数据;中位数就是把样本数据分成相同数目的两部分.其中一部分比这个数小,另一部分比这个数大的那个数;平均数就是所有样本数据的平均值,用表示;标准差是反映样本数
据分散程度大小的最常用的统计量,其计算公式如下:.有时也用标准差的平方——方差来代替标准差,实质一样.
(三)分析两个变量的相关关系时,我们可根据样本数据散点图确定两个变量之间是否存在相关关系,还可利用最小二乘法求出回归直线方程.把样本数据表示的点在直角坐标系中作出,构成的图叫做散点图.从散点图上,我们可以分析出两个变量是否存在相关关系:如果这些点大致分布在通过散点图中心的一条直线附近,那么就说这两个变量之间具有线性相关关系,这条直线叫做回归直线,直线方程叫做回归直线方程.
(四)求回归直线方程的步骤:
(1)先把数据制成表,从表中计算出,,,,.
(2)计算回归系数a,b.公式为
(3)写出回归直线方程.
(五)画样本频率分布直方图的步骤:求极差→决定组距与组数→分组→列频率分布表→画频率分布直方图.
“凡事预则立,不预则废”。科学地预习才能使我们上课听讲更有目的性和针对性。我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记。
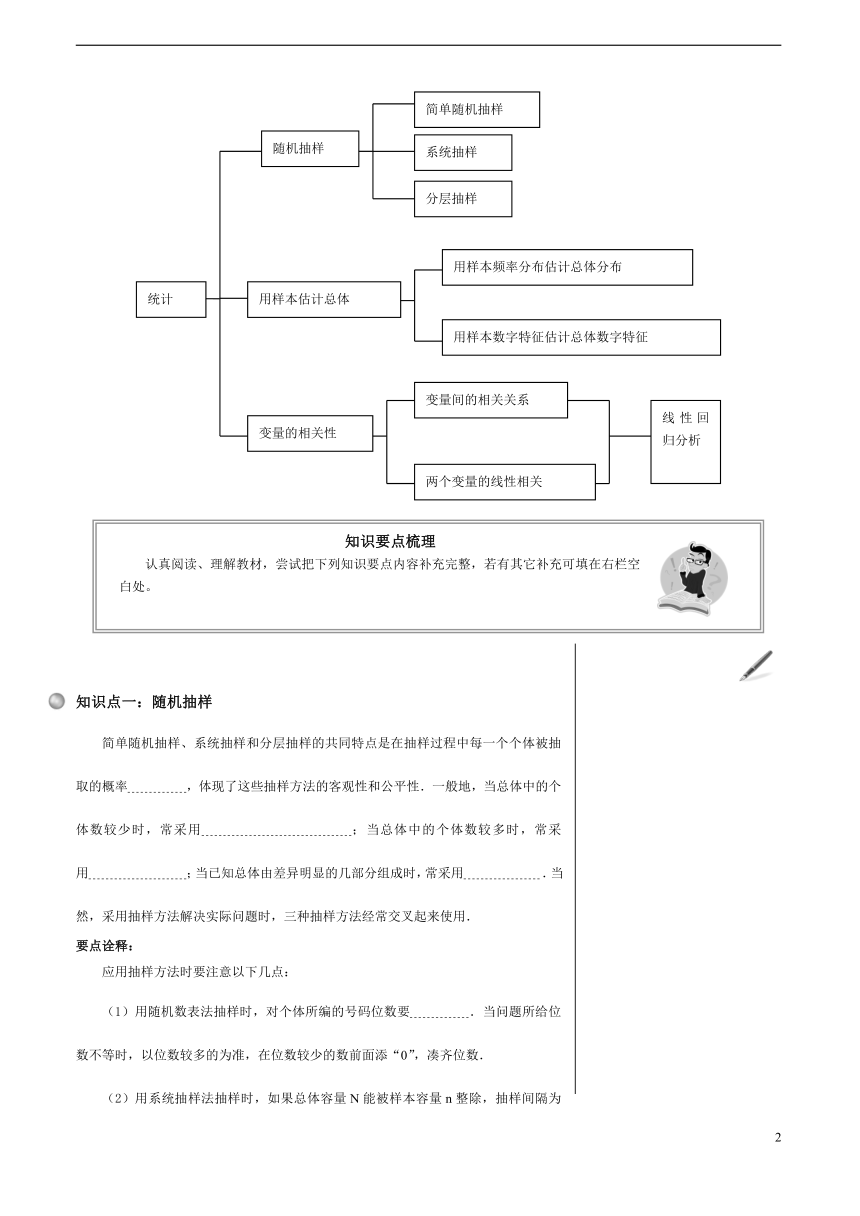
知识框图
通过知识框图,先对本单元知识要点有一个总体认识。
统计
随机抽样
简单随机抽样
系统抽样
分层抽样
用样本估计总体
用样本频率分布估计总体分布
用样本数字特征估计总体数字特征
变量的相关性
变量间的相关关系
两个变量的线性相关
线性回归分析
知识要点梳理
认真阅读、理解教材,尝试把下列知识要点内容补充完整,若有其它补充可填在右栏空白处。
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三。若有其它补充可填在右栏空白处。
总结规律和方法——强化所学
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧。
11
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
?
熟悉三种抽样方法(简单随机抽样、系统抽样、分层抽样)的特点、适用范围、实施步骤,能熟练应用三种抽样方法进行抽样.
?
熟悉数据的收集、整理、分析过程,会列频率分布表,会画频率分布直方图、折线图、茎叶图等,并能从统计图中提取有用信息,解决一些问题.
?
熟悉平均数、众数、中位数、极差、方差、标准差等各数字特征的意义,熟练掌握这些数字特征的计算或提取方法,并会由样本的数字特征对总体进行科学合理的估计,以解决一些实际问题.
?
能认识变量间的相关关系,利用散点图的直观性,进一步认识线性相关关系,了解最小二乘法思想,能由公式求回归直线方程.
重点难点:
?
重点:三种抽样方法及其应用;利用频率分布表和统计图表做统计分析;理解平均数、方差、标准差等数字特征的意义,利用样本的数字特征对总体进行合理估计,得出结论.
?
难点:抽样方法的选取和怎样用样本估计总体及对最小二乘法思想的理解.
学习策略:
本章统计部分虽然在内容与要求上比初中“统计初步”略有提高,但总的来看仍属于统计中的一些较为初步的知识.
?
注意理论联系实际,培养用数学的意识.
学数学的出发点和归宿是用数学,联系实际是本章的一个显著特点.这一章大量引入各类实际问题,要能以数学的眼光来观察所处的客观世界,逐渐养成借助助数学的思想、观点、方法来思考研究问题,解决问题,培养用数学的意识.
?
要求学会用科学计算器处理统计计算.
统计是与数据打交道的,处理问题时常计算量大而且比较复杂,如果不用科学计算器将会寸步难行.
二、学习与应用
知识点一:随机抽样
简单随机抽样、系统抽样和分层抽样的共同特点是在抽样过程中每一个个体被抽取的概率
,体现了这些抽样方法的客观性和公平性.一般地,当总体中的个体数较少时,常采用
;当总体中的个体数较多时,常采用
;当已知总体由差异明显的几部分组成时,常采用
.当然,采用抽样方法解决实际问题时,三种抽样方法经常交叉起来使用.
要点诠释:
应用抽样方法时要注意以下几点:
(1)用随机数表法抽样时,对个体所编的号码位数要
.当问题所给位数不等时,以位数较多的为准,在位数较少的数前面添“0”,凑齐位数.
(2)用系统抽样法抽样时,如果总体容量N能被样本容量n整除,抽样间隔为k=
;如果总体容量N不能被样本容量n整除,先用简单随机抽样剔除多余个体,抽样间隔k=
.
(3)用分层抽样法抽样时,分成的各层标准要
,互不
;各层
抽取的比例都
样本容量在总体中的比例,即.
知识点二:用样本估计总体
(一)用样本的频率分布估计总体分布
总体分布是指总体取值的分布规律,这种分布一般是不知晓的.我们往往用样本的频率分布去估计总体分布.一般地,样本容量越
,估计越精确,用样本频率分布去估计总体分布的基本步骤是:
(1)从总体中抽取合适的样本;
(2)分组统计样本数据;
(3)计算各组的频率,作频率分布表;
(4)画频率分布直方图.
频率分布表能使我们清楚地知道数据分布在各个小组的
,而频率分布直方图则是从各个小组数据在样本容量所占比例大小的角度来表示数据分布的规律.把频率分布直方图各个矩形的上端的中点用线段连接起来,就得到频率分布折线图.这样,通过样本频率分布就可以大致估计出总体的分布.要特别指出的是:频率分布直方图中,矩形面积=
.
在样本数据较少时,也常用茎叶图表示数据.茎叶图刻画数据有两个优点:一是所有的信息都可以从图中得到;二是茎叶图便于记录和表示.但当数据位数较多时,使用茎叶图就不够方便了.
(二)用样本的数字特征估计总体的数字特征
(1)众数、中位数和平均数都是描述数据的“
”的数字特征.它们各有优缺点,要深刻理解和把握它们在反映样本数据上的特点,结合实际情况,灵活选用.
(2)方差和标准差都是用来描述一组数据
的特征数,常用来比较两组数据的波动大小.方差较大的波动较
,方差较小的波动较
.
要点诠释:
用样本估计总体,是研究统计问题的一个基本思想方法,样本容量越
,估计越精确.
(1)当总体中的个体取不同值很少时,其频率分布表由所取的样本的不同值及相应的频率来表示,其几何表示就是相应的条形图;
(2)当总体中的个体取不同值较多时,对其频率分布的研究要用到整理样本数据的知识,列出频率分布表和区间内取值的频率分布表和频率分布直方图;
(3)当样本容量无限增大,频率分布直方图趋近于总体密度曲线.
知识点三:回归分析
(一)两个变量线性相关关系的判断
判断解释变量x与预报变量y是否具有线性相关关系,一种常见的简便可行的方法就是作出
图,从点的分布特征来判定是否线性相关:如果这些点大致分布在通过散点图中心的一条
附近,那么就说这两个变量之间具有线性相关关系,这条直线叫做回归直线.
(二)线性回归分析的方法、步骤
利用回归分析的方法对具有线性相关关系的变量进行研究的步骤为:
(1)画出两个变量的
图;
(2)求
方程;
(3)用
方程进行预报.
要点诠释:
(1)应该注意回归直线是指各样本点与此直线在整体上是最贴近的那一条直线,它只能有
条,且过样本点的中心
;
(2)其中求回归直线的方程是关键.而求回归直线的最好方法是“
法”,即对于线性回归模型y=bx+a来说,估计模型中的未知参数和的最好方法就是用最小二乘法估计和,其计算公式为,
.
类型一:抽样方法
例1.一批产品,有一级品100个,二级品60个,三级品40个,分别用系统抽样和分层抽样方法,从这批产品中抽取一容量为20的样本.
思路点拨:系统抽样适用于总体中的个体较多的情况,分层抽样适用于总体由差异明显的几部分组成的情况.
解析:
总结升华:
当总体中的个体较少时,一般可用
;
当总体中的个体较多时,一般可用
;当总体由差异明显的几部分组成时,一般可用
.而简单随机抽样作为一种最简单的抽样方法,又在其中处于一种非常重要的地位.实施简单随机抽样,主要有两种方法:
和
.
举一反三:
【变式1】把容量为100的某个样本数据分为10组,并填写频率分布表,若前七组的累积频率为0.79,而剩下三组的频数成公比大于2的整数等比数列,求剩下三组中频数最高的一组的频数?
答案:
类型二:利用频率分布表和统计图表估计总体
例2.有1个容量为100的样本,数据的分组及各组的频数如下:
;
;
;
;
;
;
.
(1)列出样本的频率分布表(含累积频率);
(2)画出频率分布直方图和累积频率分布图;
(3)根据累积频率分布估计,小于30的数据约占多大百分比.
思路点拨:按照画频率分布直方图的步骤操作,用样本的频率分布估计总体的比例.
解析:
总结升华:
举一反三:
【变式1】对某电子元件进行寿命追踪调查,情况如下:
寿命(h)
100—200
200—300
300—400
400—500
500—600
个
数
20
30
80
40
30
(1)列出频率分布表;
(2)画出频率分布直方图和累积频率分布图;
(3)估计电子元件寿命在100—400h以内的所占的百分比;
(4)估计电子元件寿命在400h以上的所占的百分比.
剖析:通过本题可掌握总体分布估计的各种方法和步骤.
答案:
类型三:用样本的数字特征估计总体
例3.从甲、乙两名运动员中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
甲:7 8 6 8 6 5 9 10 7 4
乙:9 5 7 8 7 6 8 6
7 7
(1)计算甲、乙两人射击命中环数的平均数和标准差;
(2)比较两人的成绩,然后决定选择哪一人参加比赛.
思路点拨:本题只要运用公式求出平均数和标准差即可,平均数大的水平较高.若平均数相同,标准差小的水平较稳定.
解析:
总结升华:
(1)平均数反映数据取值的
水平,平均数越大,平均水平越
.
(2)方差、标准差反映数据的
,方差、标准差越小,表示数据越
.
此类题目只要根据平均数和标准差的公式及其解答步骤求解即可.注意方差与标准差的公式区别与联系.
方差公式为
,
标准差公式为
.
举一反三:
【变式1】某班40人随机分为两组,第一组18人,第二组22人,两组学生在某次数学检测中的成绩如下表:
分
组
平均成绩
标准差
第一组
90
6
第二组
80
4
求全班的平均成绩和标准差.
思路点拨:代入方差公式s2=[(x12+x22+…+xn2)-n]即可求得.
解:
【变式2】甲、乙两人在相同的条件下,射击10次,命中环数如下:
甲:8,6,9,5,10,7,4,8,9,5;
乙:7,6,5,8,6,9,6,8,7,7.
根据以上数据估计两人的技术稳定性,结论是(
)
A.甲优于乙 B.乙优于甲 C.两人没区别 D.两人区别不大
答案:
类型四:线性回归分析
例4.下面是我国居民生活污水排放量的一组数据:
年份
1995
1996
1997
1998
1999
2000
2001
2002
排放量
151
189.1
194.8
203.8
220.9
227.7
232.3
试估计1996年我国居民生活污染排放量,并预测2004年生活污水排放量(单位:).
思路点拨:要估计或预测,可考虑先求回归直线方程.将年份与污水排放量的相关关系表达出来,可先剔除1996年,样本容量为7.
解析:
总结升华:
.
举一反三:
【变式1】某个服装店经营某种服装,在某周内获纯利(元)与该周每天销售这些服装件数之间有如下一组数据:
3
4
5
6
7
8
9
66
69
73
81
89
90
91
已知,.
(1)求,;
(2)求纯利与每天销售件数之间的回归直线方程.
解:
三、总结与测评
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力。
(一)根据简单随机抽样、系统抽样、分层抽样这三种方法的共同点、适用范围和各自特点,恰当选择抽样方法从总体中抽取样本,在选取样本时,要按照各种抽样方法的步骤抽取个体.三种抽样方法的比较如下表:
三种抽样方法比较
类别
共同点
相互联系
适用范围
各自特点
简单随机抽样
(1)抽样过程中每个个体被抽到的机会
(2)抽样过程都是
的抽样
总体中的个数较
从总体中
抽取
系统抽样
在起始部分抽样时采用简单随机抽样
总体中的个数较
将总体均分成几部分,按事先确定的规则在各部分抽取
分层抽样
每层抽样时采用简单随机抽样或系统抽样
总体由
的几部分组成
将总体分成几层,按一定的比例进行抽取
(二)用样本估计总体一般分成两种:一种是用样本的频率分布估计总体的分布;另一种是用样本的数字特征(如平均数、标准差等)估计总体的数字特征.
所谓第一种就是利用样本的频率分布表和频率分布直方图对总体情况作出估计,有时也利用频率分布折线图和茎叶图对总体估计.直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到在分布表中看不清楚的数据模式,这样根据样本的频率分布,我们可以大致估计出总体的分布.但是,当总体的个体数较多时,所需抽样的样本容量也不能太小,随着样本容量的增加,频率分布折线图会越来越接近于一条光滑曲线,统计中称这条曲线为总体密度曲线,它能给我们提供更加精细的信息.在样本数据较少时,用茎叶图表示数据的效果较好,它不但可以保留所有信息,而且可以随时记录,这对数据的记录和表示都能带来方便.
所谓第二种就是为了从整体上更好地把握总体的规律,我们还可以通过样本数据的众数、中位数、平均数和标准差等数字特征对总体的数字特征作出估计.众数就是样本数据中出现最多的数据;中位数就是把样本数据分成相同数目的两部分.其中一部分比这个数小,另一部分比这个数大的那个数;平均数就是所有样本数据的平均值,用表示;标准差是反映样本数
据分散程度大小的最常用的统计量,其计算公式如下:.有时也用标准差的平方——方差来代替标准差,实质一样.
(三)分析两个变量的相关关系时,我们可根据样本数据散点图确定两个变量之间是否存在相关关系,还可利用最小二乘法求出回归直线方程.把样本数据表示的点在直角坐标系中作出,构成的图叫做散点图.从散点图上,我们可以分析出两个变量是否存在相关关系:如果这些点大致分布在通过散点图中心的一条直线附近,那么就说这两个变量之间具有线性相关关系,这条直线叫做回归直线,直线方程叫做回归直线方程.
(四)求回归直线方程的步骤:
(1)先把数据制成表,从表中计算出,,,,.
(2)计算回归系数a,b.公式为
(3)写出回归直线方程.
(五)画样本频率分布直方图的步骤:求极差→决定组距与组数→分组→列频率分布表→画频率分布直方图.
“凡事预则立,不预则废”。科学地预习才能使我们上课听讲更有目的性和针对性。我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记。
知识框图
通过知识框图,先对本单元知识要点有一个总体认识。
统计
随机抽样
简单随机抽样
系统抽样
分层抽样
用样本估计总体
用样本频率分布估计总体分布
用样本数字特征估计总体数字特征
变量的相关性
变量间的相关关系
两个变量的线性相关
线性回归分析
知识要点梳理
认真阅读、理解教材,尝试把下列知识要点内容补充完整,若有其它补充可填在右栏空白处。
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三。若有其它补充可填在右栏空白处。
总结规律和方法——强化所学
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧。
11
