人教版七年级数学下册第十八章 全等三角形单元练习(含答案)
文档属性
| 名称 | 人教版七年级数学下册第十八章 全等三角形单元练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 308.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 00:00:00 | ||
图片预览


文档简介
第十八章
全等三角形
一、单选题
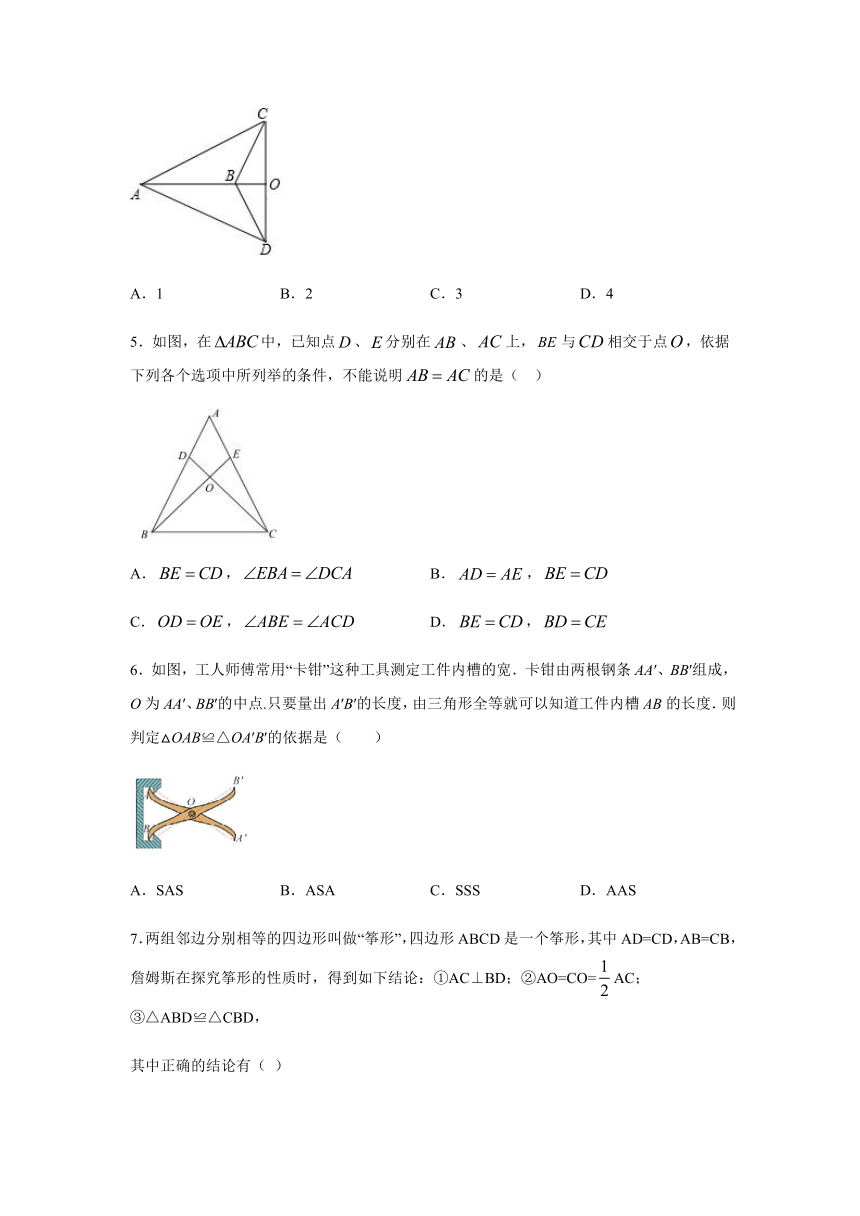
1.如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则BE的长是
A.1
B.2
C.4
D.6
2.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是(
)
A.
B.
C.
D.
3.如果两个三角形全等,那么下列结论正确的是(
)
A.这两个三角形是直角三角形
B.这两个三角形都是锐角三角形
C.这两个三角形的面积相等
D.这两个三角形是钝角三角形
4.如图,射线AB交CD于O,AC=AD,BC=BD,则图中全等三角形的对数是( )
A.1
B.2
C.3
D.4
5.如图,在中,已知点、分别在、上,与相交于点,依据下列各个选项中所列举的条件,不能说明的是(
)
A.,
B.,
C.,
D.,
6.如图,工人师傅常用“卡钳”这种工具测定工件内槽的宽.卡钳由两根钢条AA′、BB′组成,O为AA′、BB′的中点.只要量出A′B′的长度,由三角形全等就可以知道工件内槽AB的长度.则判定△OAB≌△OA′B′的依据是(
)
A.SAS
B.ASA
C.SSS
D.AAS
7.两组邻边分别相等的四边形叫做“筝形”,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,
其中正确的结论有(
)
A.0个
B.1个
C.2个
D.3个
8.如图,在中,,的平分线交于点.若,则点到的距离为( )
A.1
B.
C.
D.2
9.如图,在△ABC中,CD平分∠ACB交AB于点D,于点E,于点F,且BC=4,DE=2,则△BCD的面积是(
)
A.4
B.2
C.8
D.6
10.已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A.①正确,②错误
B.①错误,②正确
C.①,②都错误
D.①,②都正确
二、填空题
11.如图,B,D,E,C在一条直线上,且,若,则__________.
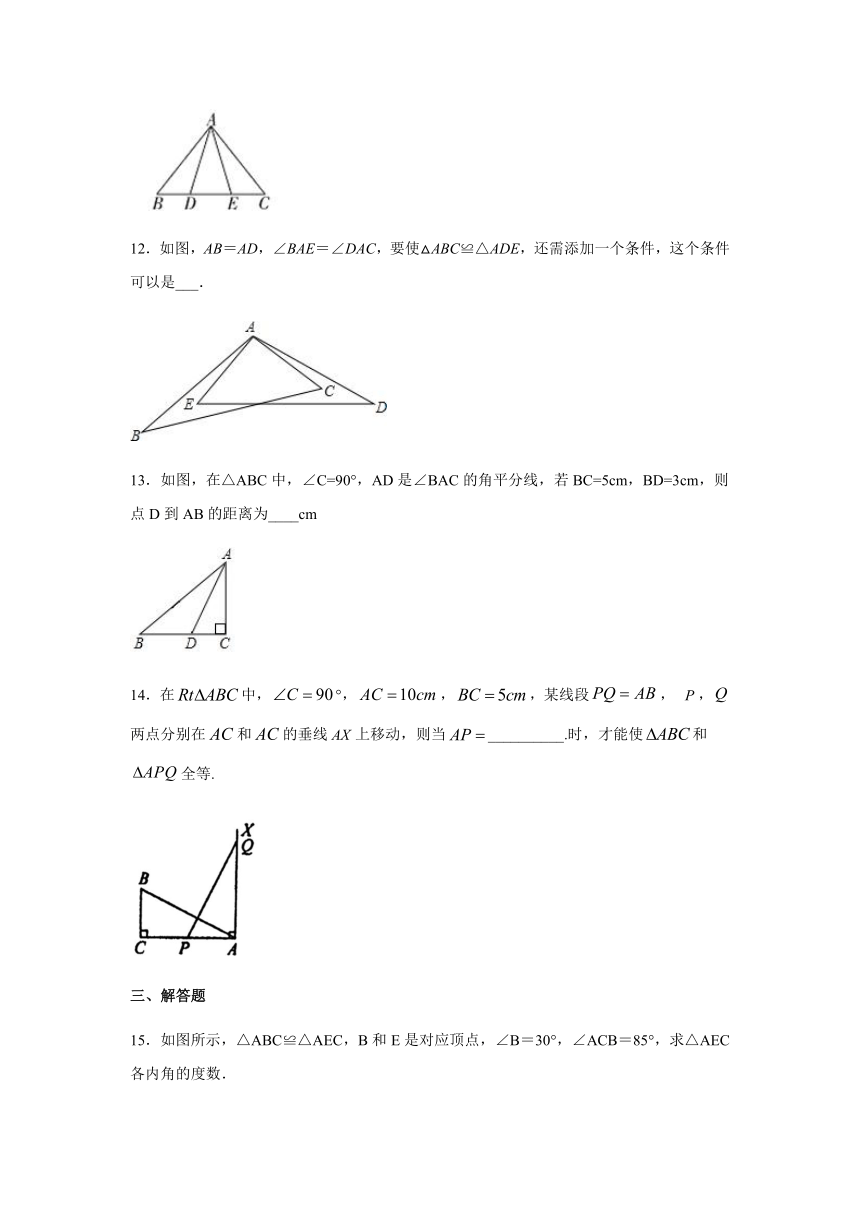
12.如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是___.
13.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5cm,BD=3cm,则点D到AB的距离为____cm
14.在中,°,,,某线段,
,两点分别在和的垂线上移动,则当__________.时,才能使和全等.
三、解答题
15.如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,求△AEC各内角的度数.
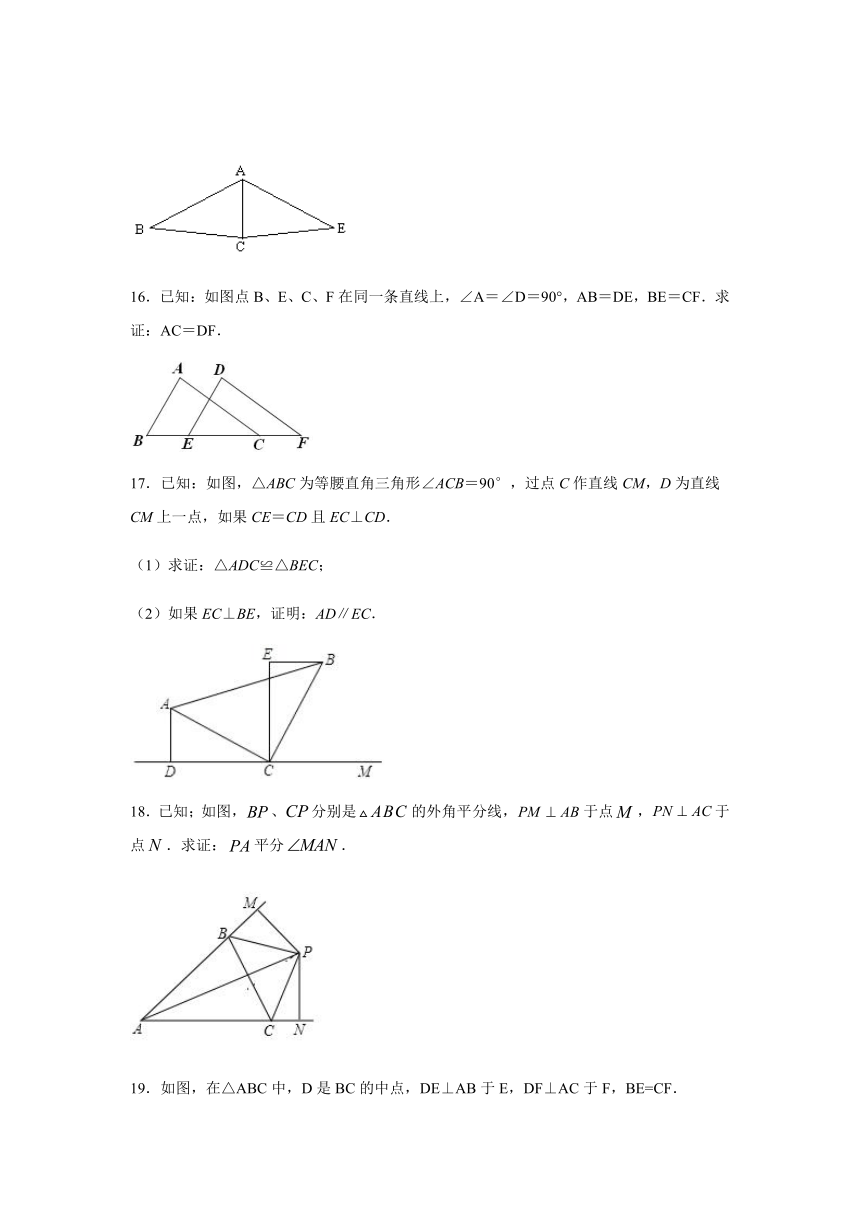
16.已知:如图点B、E、C、F在同一条直线上,∠A=∠D=90°,AB=DE,BE=CF.求证:AC=DF.
17.已知:如图,△ABC为等腰直角三角形∠ACB=90°,过点C作直线CM,D为直线CM上一点,如果CE=CD且EC⊥CD.
(1)求证:△ADC≌△BEC;
(2)如果EC⊥BE,证明:AD∥EC.
18.已知;如图,、分别是的外角平分线,于点,于点.求证:平分.
19.如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
(1)求证:AD平分∠BAC;
(2)连接EF,求证:AD垂直平分EF.
答案
1.B
2.D
3.C
4.C
5.B
6.A
7.D
8.D
9.A
10.D
11.30°
12.AE=AC.
13.2cm
14.5㎝或10㎝
15.解:∵△ABC≌△AEC,∴∠B=∠E=30°,∠ACB=∠ACE=85°,
∴∠EAC=65°.
16证明:∵
∴
即:
∵
∴和为直角三角形
在和中
∴
∴
17.(1)∵EC⊥DM,
∴∠ECD=90°,
∴∠ACB=∠DCE=90°,
∴∠ACD+∠ACE=90°,∠BCE+∠ACE=90°,
∴∠ACD=∠BCE,
∵CD=CE,CA=CB,
∴△ADC≌△BEC(SAS).
(2)由(1)得△ADC≌△BEC,
∵EC⊥BE,
∴∠ADC=∠E=90°,
∴AD⊥DM,
∵EC⊥DM,
∴AD∥EC.
18.作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,又PM⊥AB,PN⊥AC,
∴PA平分∠MAN.
19.(1)∵D是BC的中点
∴BD=CD,
又∵BE=CF,DE⊥AB,DF⊥AC,
∴DE=DF,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC;
(2)
∴∠B=∠C,
∴AB=AC,
∵BE=CF,
∴AB?BE=AC?CF,
∴AE=AF,
∵DE=DF,
∴AD垂直平分EF
全等三角形
一、单选题
1.如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则BE的长是
A.1
B.2
C.4
D.6
2.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是(
)
A.
B.
C.
D.
3.如果两个三角形全等,那么下列结论正确的是(
)
A.这两个三角形是直角三角形
B.这两个三角形都是锐角三角形
C.这两个三角形的面积相等
D.这两个三角形是钝角三角形
4.如图,射线AB交CD于O,AC=AD,BC=BD,则图中全等三角形的对数是( )
A.1
B.2
C.3
D.4
5.如图,在中,已知点、分别在、上,与相交于点,依据下列各个选项中所列举的条件,不能说明的是(
)
A.,
B.,
C.,
D.,
6.如图,工人师傅常用“卡钳”这种工具测定工件内槽的宽.卡钳由两根钢条AA′、BB′组成,O为AA′、BB′的中点.只要量出A′B′的长度,由三角形全等就可以知道工件内槽AB的长度.则判定△OAB≌△OA′B′的依据是(
)
A.SAS
B.ASA
C.SSS
D.AAS
7.两组邻边分别相等的四边形叫做“筝形”,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,
其中正确的结论有(
)
A.0个
B.1个
C.2个
D.3个
8.如图,在中,,的平分线交于点.若,则点到的距离为( )
A.1
B.
C.
D.2
9.如图,在△ABC中,CD平分∠ACB交AB于点D,于点E,于点F,且BC=4,DE=2,则△BCD的面积是(
)
A.4
B.2
C.8
D.6
10.已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A.①正确,②错误
B.①错误,②正确
C.①,②都错误
D.①,②都正确
二、填空题
11.如图,B,D,E,C在一条直线上,且,若,则__________.
12.如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是___.
13.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5cm,BD=3cm,则点D到AB的距离为____cm
14.在中,°,,,某线段,
,两点分别在和的垂线上移动,则当__________.时,才能使和全等.
三、解答题
15.如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,求△AEC各内角的度数.
16.已知:如图点B、E、C、F在同一条直线上,∠A=∠D=90°,AB=DE,BE=CF.求证:AC=DF.
17.已知:如图,△ABC为等腰直角三角形∠ACB=90°,过点C作直线CM,D为直线CM上一点,如果CE=CD且EC⊥CD.
(1)求证:△ADC≌△BEC;
(2)如果EC⊥BE,证明:AD∥EC.
18.已知;如图,、分别是的外角平分线,于点,于点.求证:平分.
19.如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
(1)求证:AD平分∠BAC;
(2)连接EF,求证:AD垂直平分EF.
答案
1.B
2.D
3.C
4.C
5.B
6.A
7.D
8.D
9.A
10.D
11.30°
12.AE=AC.
13.2cm
14.5㎝或10㎝
15.解:∵△ABC≌△AEC,∴∠B=∠E=30°,∠ACB=∠ACE=85°,
∴∠EAC=65°.
16证明:∵
∴
即:
∵
∴和为直角三角形
在和中
∴
∴
17.(1)∵EC⊥DM,
∴∠ECD=90°,
∴∠ACB=∠DCE=90°,
∴∠ACD+∠ACE=90°,∠BCE+∠ACE=90°,
∴∠ACD=∠BCE,
∵CD=CE,CA=CB,
∴△ADC≌△BEC(SAS).
(2)由(1)得△ADC≌△BEC,
∵EC⊥BE,
∴∠ADC=∠E=90°,
∴AD⊥DM,
∵EC⊥DM,
∴AD∥EC.
18.作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,又PM⊥AB,PN⊥AC,
∴PA平分∠MAN.
19.(1)∵D是BC的中点
∴BD=CD,
又∵BE=CF,DE⊥AB,DF⊥AC,
∴DE=DF,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC;
(2)
∴∠B=∠C,
∴AB=AC,
∵BE=CF,
∴AB?BE=AC?CF,
∴AE=AF,
∵DE=DF,
∴AD垂直平分EF
