北师大版七下数学第四章 三角形回顾与思考(1) 教案
文档属性
| 名称 | 北师大版七下数学第四章 三角形回顾与思考(1) 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 17.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 21:13:33 | ||
图片预览


文档简介
北师大版七年级下册
第四章 三角形
回顾与思考(一)
教学目标:(熟悉知识要点)
1.三角形
(1)三角形三边关系
(2)三角形内角和定理
(3)三条重要线段
(4)角平分线.中线.高线
2.
全等三角形
(1)全等图形的概念
(2)全等三角形的性质
(3)全等三角形的判定条件①SSS.②SAS.③ASA.④AAS
(4)全等三角形的应用→利用全等三角形测距离
3.作三角形
教学重点
三角形全等的条件及其应用.
尺规作图
教学难点
两个三角形全等的应用.
教学过程
一.基础知识梳理(复习回答)
1.三角形中的主要线段指
,
它们都有
条,并且它们或它们所在直线会
.
2.锐角三角形的三条高都在
,钝角三角形有
条高在三角形外,
直角三角形有两条高恰是它的
.
3.三角形三边的关系:
.
4.三角形具有
性,
四边形不具有
性.
二.基础训练(评析)
1、已知一个三角形的三边长为3、8、x,则x
的取值范围是
。
2、已知一个三角形的三边长3、
a+2、8,则a的取值范围是
。
3.等腰三角形一边的长是5
,另一边的长是8,则它的周长是
.
4.一个三角形的两边长分别是2cm和9cm
,第三边的长为奇数,则第三边的长为
.
5.如图,
AD、AF
分别是△ABC的高和角平线,
∠C=76o,
∠B=36o,
则∠DAF
=______o.
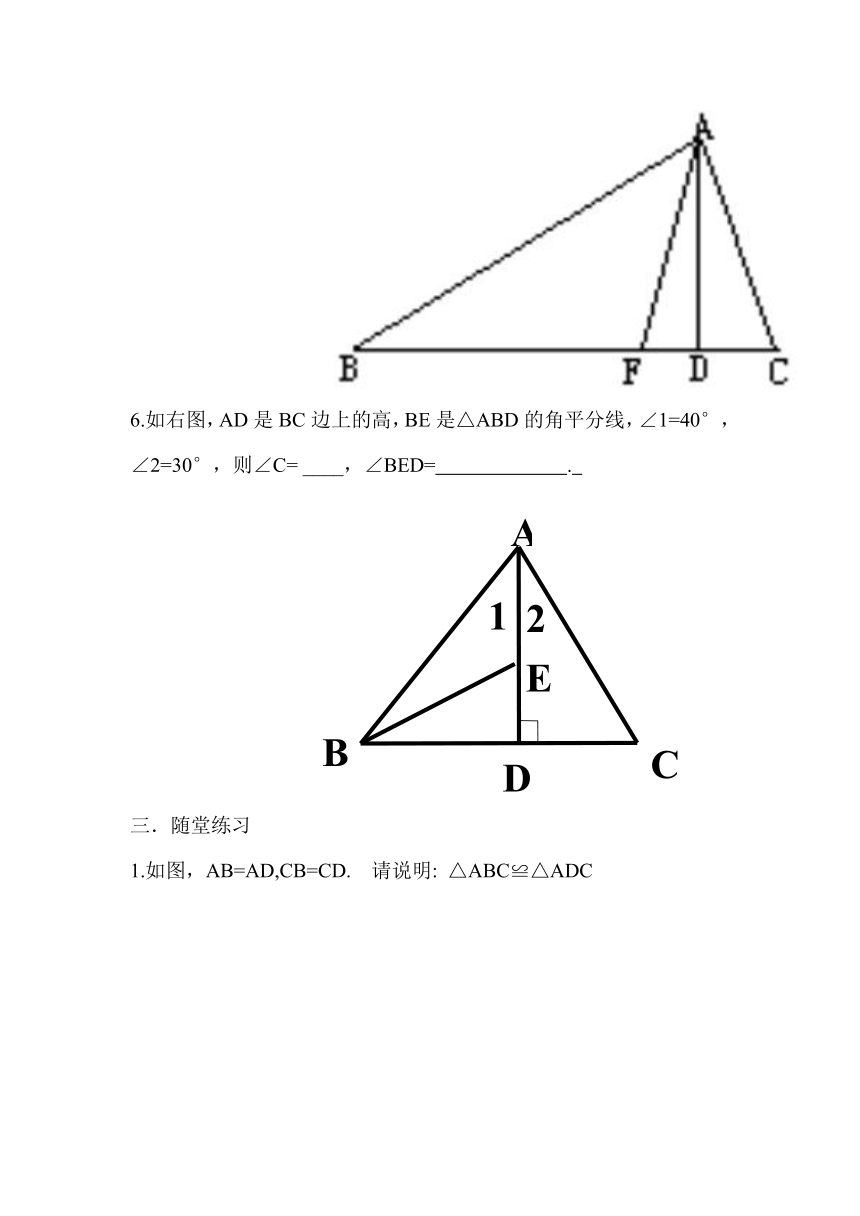
6.如右图,AD是BC边上的高,BE是△ABD的角平分线,∠1=40°,∠2=30°,则∠C=
____,∠BED=
.
三.随堂练习
1.如图,AB=AD,CB=CD.
请说明:
△ABC≌△ADC
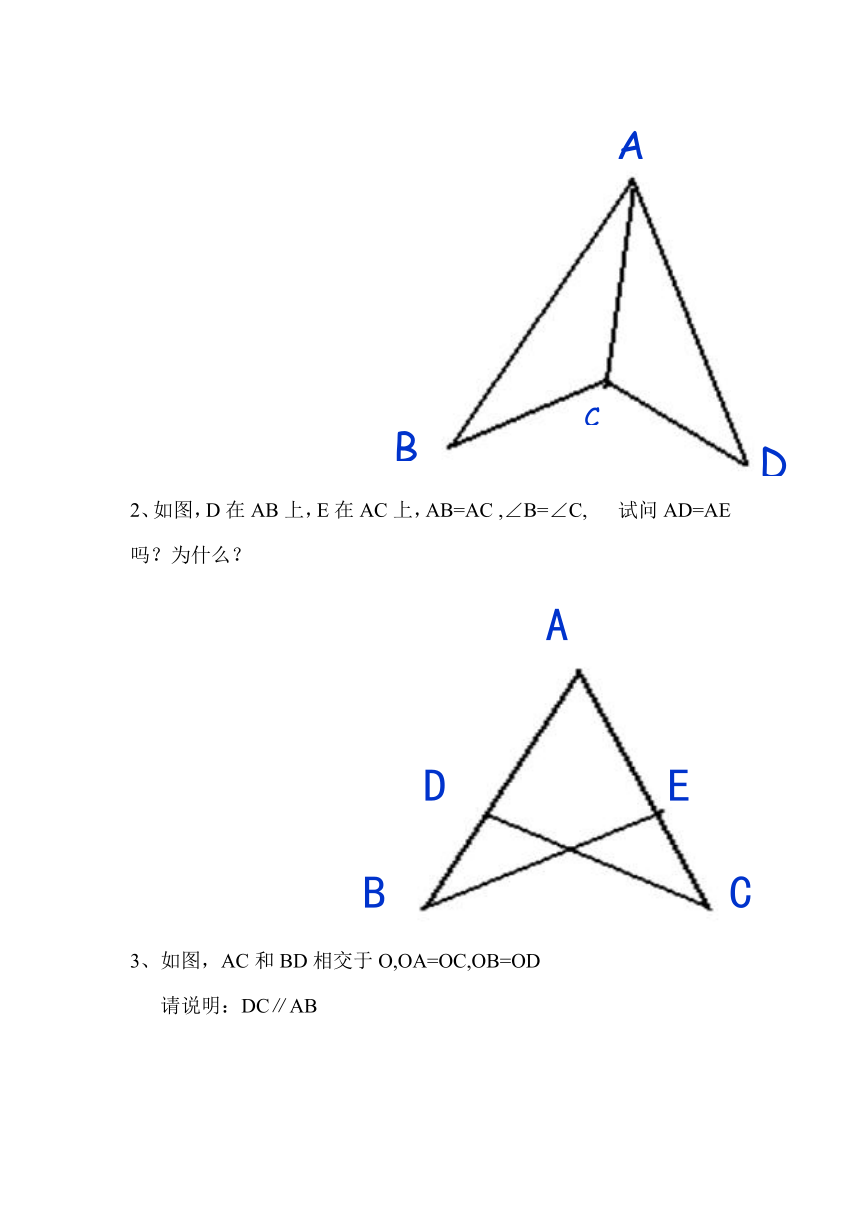
2、如图,D在AB上,E在AC上,AB=AC
,∠B=∠C,
试问AD=AE吗?为什么?
3、如图,AC和BD相交于O,OA=OC,OB=OD
请说明:DC∥AB
4、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
四.达标测评
1、等腰三角形一边的长是
5
,另一边的长是8,则它的周
长是
。
2、一个三角形的两边长是3、5,则它周长的范围是
。
3、如图,已知:AD是△ABC
的中线,△ABC的面积为
80cm2,则△ABD的面积是
.
4、同上题图,
若△ACD的面积30cm2,则△ABC的面积为
.
5、如图,在△ABC中,CE,BF是两条高,若∠A=
70°,∠BCE=25°,则∠EBF的度数是
,∠FBC的度数是
6、若三角形三个内角的度数
之比为
2∶3∶4,则这三个内角的度数分别是
7、在△ABC中,∠B=400,∠A∶∠C=3∶4,∠C=
.
8、如图,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=1200,那么∠A的度数是
.
五.巩固提高
1.在△ABC中,
∠A=40°,∠B=∠C,则∠C= .
2.一个三角形三个内角度数的比是2:3:4,那么这个三角形是 _______三角形.
3.在△ABC中,
∠A-
∠B=
36o,∠C=2∠B,则∠A= ,∠B= ,∠C= .
4、如图,要判断△ABE≌△ACD,除去公共角∠A外,在下列横线上,写出还需的两个条件,并在括号内写出这些条件判定三角形全等的依据
(1)
∠B=∠C,AB=AC(ASA);
(2)
,
(
);
(3)
,
(
).
5、如图1,已知AC=BD,∠1=∠2,那么△ABC≌
,其判定根据是__________。
6.如右图,已知AC=BD,
∠A
=∠D
,请你添一个直接条件,______=
_____,使△AFC≌△DEB.
六.课堂小结
交流本节课的收获,说说存在的困惑
七.布置作业
第四章
复习题
第2.3.4.5.6.7题
E
2
1
C
B
A
D
B
C
D
A
A
B
C
D
E
C
B
D
O
A
D
E
2
1
B
A
C
D
C
B
A
F
E
C
B
A
O
E
D
C
B
A
C
D
E
B
A
第四章 三角形
回顾与思考(一)
教学目标:(熟悉知识要点)
1.三角形
(1)三角形三边关系
(2)三角形内角和定理
(3)三条重要线段
(4)角平分线.中线.高线
2.
全等三角形
(1)全等图形的概念
(2)全等三角形的性质
(3)全等三角形的判定条件①SSS.②SAS.③ASA.④AAS
(4)全等三角形的应用→利用全等三角形测距离
3.作三角形
教学重点
三角形全等的条件及其应用.
尺规作图
教学难点
两个三角形全等的应用.
教学过程
一.基础知识梳理(复习回答)
1.三角形中的主要线段指
,
它们都有
条,并且它们或它们所在直线会
.
2.锐角三角形的三条高都在
,钝角三角形有
条高在三角形外,
直角三角形有两条高恰是它的
.
3.三角形三边的关系:
.
4.三角形具有
性,
四边形不具有
性.
二.基础训练(评析)
1、已知一个三角形的三边长为3、8、x,则x
的取值范围是
。
2、已知一个三角形的三边长3、
a+2、8,则a的取值范围是
。
3.等腰三角形一边的长是5
,另一边的长是8,则它的周长是
.
4.一个三角形的两边长分别是2cm和9cm
,第三边的长为奇数,则第三边的长为
.
5.如图,
AD、AF
分别是△ABC的高和角平线,
∠C=76o,
∠B=36o,
则∠DAF
=______o.
6.如右图,AD是BC边上的高,BE是△ABD的角平分线,∠1=40°,∠2=30°,则∠C=
____,∠BED=
.
三.随堂练习
1.如图,AB=AD,CB=CD.
请说明:
△ABC≌△ADC
2、如图,D在AB上,E在AC上,AB=AC
,∠B=∠C,
试问AD=AE吗?为什么?
3、如图,AC和BD相交于O,OA=OC,OB=OD
请说明:DC∥AB
4、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
四.达标测评
1、等腰三角形一边的长是
5
,另一边的长是8,则它的周
长是
。
2、一个三角形的两边长是3、5,则它周长的范围是
。
3、如图,已知:AD是△ABC
的中线,△ABC的面积为
80cm2,则△ABD的面积是
.
4、同上题图,
若△ACD的面积30cm2,则△ABC的面积为
.
5、如图,在△ABC中,CE,BF是两条高,若∠A=
70°,∠BCE=25°,则∠EBF的度数是
,∠FBC的度数是
6、若三角形三个内角的度数
之比为
2∶3∶4,则这三个内角的度数分别是
7、在△ABC中,∠B=400,∠A∶∠C=3∶4,∠C=
.
8、如图,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=1200,那么∠A的度数是
.
五.巩固提高
1.在△ABC中,
∠A=40°,∠B=∠C,则∠C= .
2.一个三角形三个内角度数的比是2:3:4,那么这个三角形是 _______三角形.
3.在△ABC中,
∠A-
∠B=
36o,∠C=2∠B,则∠A= ,∠B= ,∠C= .
4、如图,要判断△ABE≌△ACD,除去公共角∠A外,在下列横线上,写出还需的两个条件,并在括号内写出这些条件判定三角形全等的依据
(1)
∠B=∠C,AB=AC(ASA);
(2)
,
(
);
(3)
,
(
).
5、如图1,已知AC=BD,∠1=∠2,那么△ABC≌
,其判定根据是__________。
6.如右图,已知AC=BD,
∠A
=∠D
,请你添一个直接条件,______=
_____,使△AFC≌△DEB.
六.课堂小结
交流本节课的收获,说说存在的困惑
七.布置作业
第四章
复习题
第2.3.4.5.6.7题
E
2
1
C
B
A
D
B
C
D
A
A
B
C
D
E
C
B
D
O
A
D
E
2
1
B
A
C
D
C
B
A
F
E
C
B
A
O
E
D
C
B
A
C
D
E
B
A
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
