人教版八年级上册数学一课一练12.2.1 三角形全等的判定(一)SSS(含解析)
文档属性
| 名称 | 人教版八年级上册数学一课一练12.2.1 三角形全等的判定(一)SSS(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 20:51:06 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学一课一练
12.2
三角形全等的判定
第1课时
三角形全等的判定(一)SSS
01课前预习
要点感知1
三边分别相等的两个三角形_______(可以简写成“_______”或“_______”).
预习练习1-1
如图,下列三角形中,与△ABC全等的是_______.
要点感知2
用无刻度的直尺和圆规作图的方法称为尺规作图.
预习练习2-1
已知∠α,求作∠AOB,使∠AOB=∠α(不写作法,保留作图痕迹).
02当堂训练
知识点1
用“SSS”判定两个三角形全等
1.已知,如图,在△ABC和△BAD中,BC=AD,AC=BD,求证:△ABC≌△BAD.
2.如图所示,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB,求证:△ABC≌△FDE.
3.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,求证:△ABD≌△ACD.
知识点2
三角形全等的判定与性质的综合
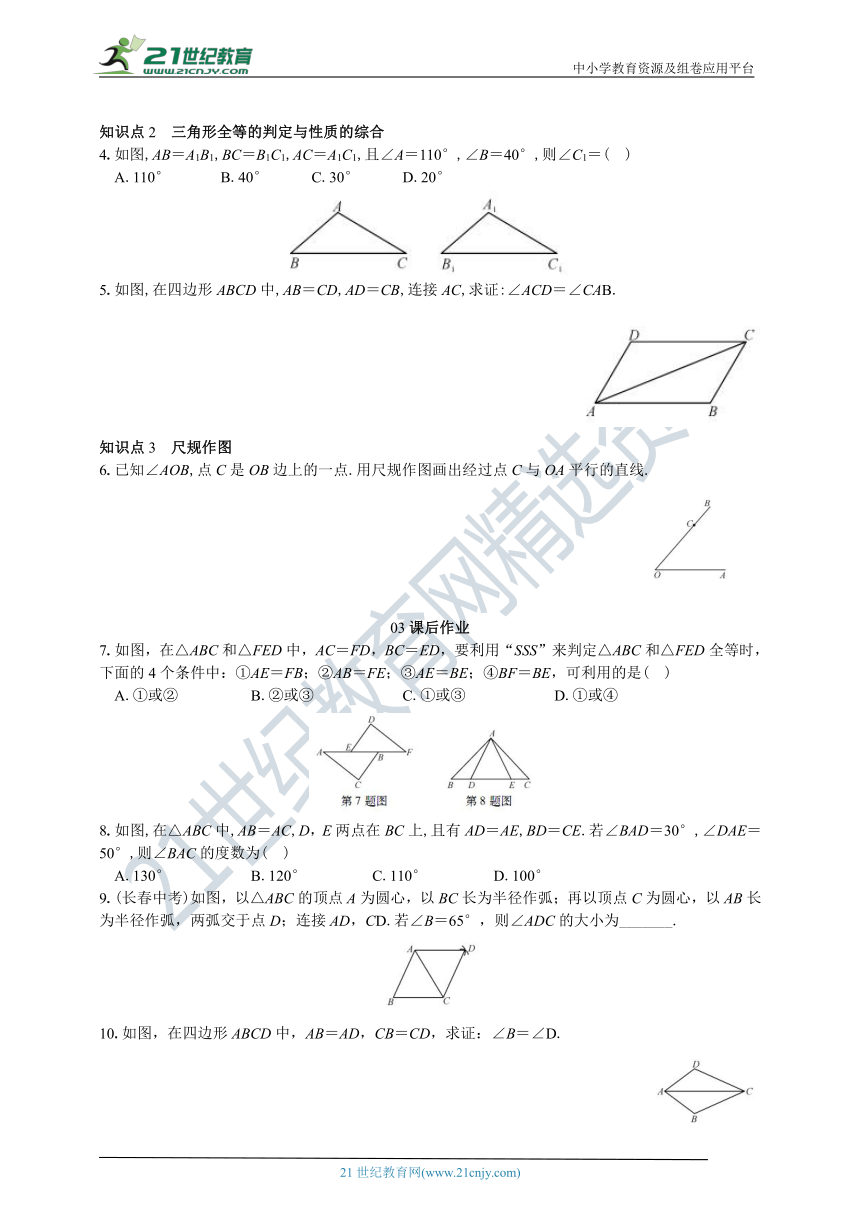
4.如图,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=(
)
A.110°
B.40°
C.30°
D.20°
5.如图,在四边形ABCD中,AB=CD,AD=CB,连接AC,求证:∠ACD=∠CAB.
知识点3
尺规作图
6.已知∠AOB,点C是OB边上的一点.用尺规作图画出经过点C与OA平行的直线.
03课后作业
7.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是(
)
A.①或②
B.②或③
C.①或③
D.①或④
8.如图,在△ABC中,AB=AC,D,E两点在BC上,且有AD=AE,BD=CE.若∠BAD=30°,∠DAE=50°,则∠BAC的度数为(
)
A.130°
B.120°
C.110°
D.100°
9.(长春中考)如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD,CD.若∠B=65°,则∠ADC的大小为_______.
10.如图,在四边形ABCD中,AB=AD,CB=CD,求证:∠B=∠D.
11.如图,AB=AC,DB=DC,EB=EC.
(1)图中有几对全等三角形?请一一写出来.
(2)选择(1)中的一对全等三角形加以证明.
12.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
13.如图,已知AB=AC,AD=AE,BD=CE,
求证:∠3=∠1+∠2.
挑战自我
14.(佛山中考)如图,已知AB=DC,DB=AC.
(1)求证:∠B=∠C;(注:证明过程要求给出每一步结论成立的依据)
(2)在(1)的证明过程中,需要作辅助线,它的意图是什么?
参考答案
课前预习
要点感知1
全等
边边边
SSS
预习练习1-1
③
预习练习2-1
略.
当堂训练
1.证明:在△ABC和△BAD中,BC=AD,AC=BD,AB=BA(公共边),∴△ABC≌△BAD(SSS).
2.证明:∵AD=FB,∴AD+DB=FB+DB,即AB=FD.在△ABC与△FDE中,AC=FE,AB=FD,BC=DE,∴△ABC≌△FDE.
3.证明:∵AD是BC边上的中线,∴BD=CD.在△ABD和△ACD中,AB=AC,AD=AD(公共边),BD=CD,
∴△ABD≌△ACD(SSS).
4.C
5.证明:在△ADC与△CBA中,AB=CD,AD=CB,AC=CA,∴△ADC≌△CBA(SSS).∴∠ACD=∠CAB.
6.作图略,提示:以点C为顶点,作一个角等于∠AOB.
课后作业
7.A
8.C
9.65°
10.证明:在△ABC和△ADC中,AB=AD,CB=CD,
AC=AC,∴△ABC≌△ADC(SSS).∴∠B=∠D.
11.(1)△ABD≌△ACD,△ABE≌△ACE,△DBE≌△DCE.(2)以△ABD≌△ACD为例:证明:在△ABD与△ACD中,AB=AC,
DB=DC,AD=AD,∴△ABD≌△ACD(SSS).
12.∠BAD=∠CAD.理由:∵AB=AC,AE=AB,AF=AC,∴AE=AF.在△AOE和AOF中,AO=AO,
AE=AF,OE=OF,∴△AOE≌△AOF(SSS).∴∠EAO=∠FAO,即∠BAD=∠CAD.
13.证明:在△ABD和△ACE中,AB=AC,AD=AE,
BD=CE,∴△ABD≌△ACE(SSS).∴∠BAD=∠1,∠ABD=∠2.∵∠3=∠BAD+∠ABD,∴∠3=∠1+∠2.
14.(1)证明:连接AD,在△BAD和△CDA中,AB=CD(已知),DB=AC(已知),
AD=DA(公共边),∴△BAD≌△CDA(SSS).∴∠B=∠C(全等三角形的对应角相等).(2)作辅助线的意图是构造全等的三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级上册数学一课一练
12.2
三角形全等的判定
第1课时
三角形全等的判定(一)SSS
01课前预习
要点感知1
三边分别相等的两个三角形_______(可以简写成“_______”或“_______”).
预习练习1-1
如图,下列三角形中,与△ABC全等的是_______.
要点感知2
用无刻度的直尺和圆规作图的方法称为尺规作图.
预习练习2-1
已知∠α,求作∠AOB,使∠AOB=∠α(不写作法,保留作图痕迹).
02当堂训练
知识点1
用“SSS”判定两个三角形全等
1.已知,如图,在△ABC和△BAD中,BC=AD,AC=BD,求证:△ABC≌△BAD.
2.如图所示,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB,求证:△ABC≌△FDE.
3.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,求证:△ABD≌△ACD.
知识点2
三角形全等的判定与性质的综合
4.如图,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=(
)
A.110°
B.40°
C.30°
D.20°
5.如图,在四边形ABCD中,AB=CD,AD=CB,连接AC,求证:∠ACD=∠CAB.
知识点3
尺规作图
6.已知∠AOB,点C是OB边上的一点.用尺规作图画出经过点C与OA平行的直线.
03课后作业
7.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是(
)
A.①或②
B.②或③
C.①或③
D.①或④
8.如图,在△ABC中,AB=AC,D,E两点在BC上,且有AD=AE,BD=CE.若∠BAD=30°,∠DAE=50°,则∠BAC的度数为(
)
A.130°
B.120°
C.110°
D.100°
9.(长春中考)如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD,CD.若∠B=65°,则∠ADC的大小为_______.
10.如图,在四边形ABCD中,AB=AD,CB=CD,求证:∠B=∠D.
11.如图,AB=AC,DB=DC,EB=EC.
(1)图中有几对全等三角形?请一一写出来.
(2)选择(1)中的一对全等三角形加以证明.
12.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
13.如图,已知AB=AC,AD=AE,BD=CE,
求证:∠3=∠1+∠2.
挑战自我
14.(佛山中考)如图,已知AB=DC,DB=AC.
(1)求证:∠B=∠C;(注:证明过程要求给出每一步结论成立的依据)
(2)在(1)的证明过程中,需要作辅助线,它的意图是什么?
参考答案
课前预习
要点感知1
全等
边边边
SSS
预习练习1-1
③
预习练习2-1
略.
当堂训练
1.证明:在△ABC和△BAD中,BC=AD,AC=BD,AB=BA(公共边),∴△ABC≌△BAD(SSS).
2.证明:∵AD=FB,∴AD+DB=FB+DB,即AB=FD.在△ABC与△FDE中,AC=FE,AB=FD,BC=DE,∴△ABC≌△FDE.
3.证明:∵AD是BC边上的中线,∴BD=CD.在△ABD和△ACD中,AB=AC,AD=AD(公共边),BD=CD,
∴△ABD≌△ACD(SSS).
4.C
5.证明:在△ADC与△CBA中,AB=CD,AD=CB,AC=CA,∴△ADC≌△CBA(SSS).∴∠ACD=∠CAB.
6.作图略,提示:以点C为顶点,作一个角等于∠AOB.
课后作业
7.A
8.C
9.65°
10.证明:在△ABC和△ADC中,AB=AD,CB=CD,
AC=AC,∴△ABC≌△ADC(SSS).∴∠B=∠D.
11.(1)△ABD≌△ACD,△ABE≌△ACE,△DBE≌△DCE.(2)以△ABD≌△ACD为例:证明:在△ABD与△ACD中,AB=AC,
DB=DC,AD=AD,∴△ABD≌△ACD(SSS).
12.∠BAD=∠CAD.理由:∵AB=AC,AE=AB,AF=AC,∴AE=AF.在△AOE和AOF中,AO=AO,
AE=AF,OE=OF,∴△AOE≌△AOF(SSS).∴∠EAO=∠FAO,即∠BAD=∠CAD.
13.证明:在△ABD和△ACE中,AB=AC,AD=AE,
BD=CE,∴△ABD≌△ACE(SSS).∴∠BAD=∠1,∠ABD=∠2.∵∠3=∠BAD+∠ABD,∴∠3=∠1+∠2.
14.(1)证明:连接AD,在△BAD和△CDA中,AB=CD(已知),DB=AC(已知),
AD=DA(公共边),∴△BAD≌△CDA(SSS).∴∠B=∠C(全等三角形的对应角相等).(2)作辅助线的意图是构造全等的三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
