人教版八年级上册数学一课一练12.2.2 三角形全等的判定(二)SAS(含解析)
文档属性
| 名称 | 人教版八年级上册数学一课一练12.2.2 三角形全等的判定(二)SAS(含解析) | 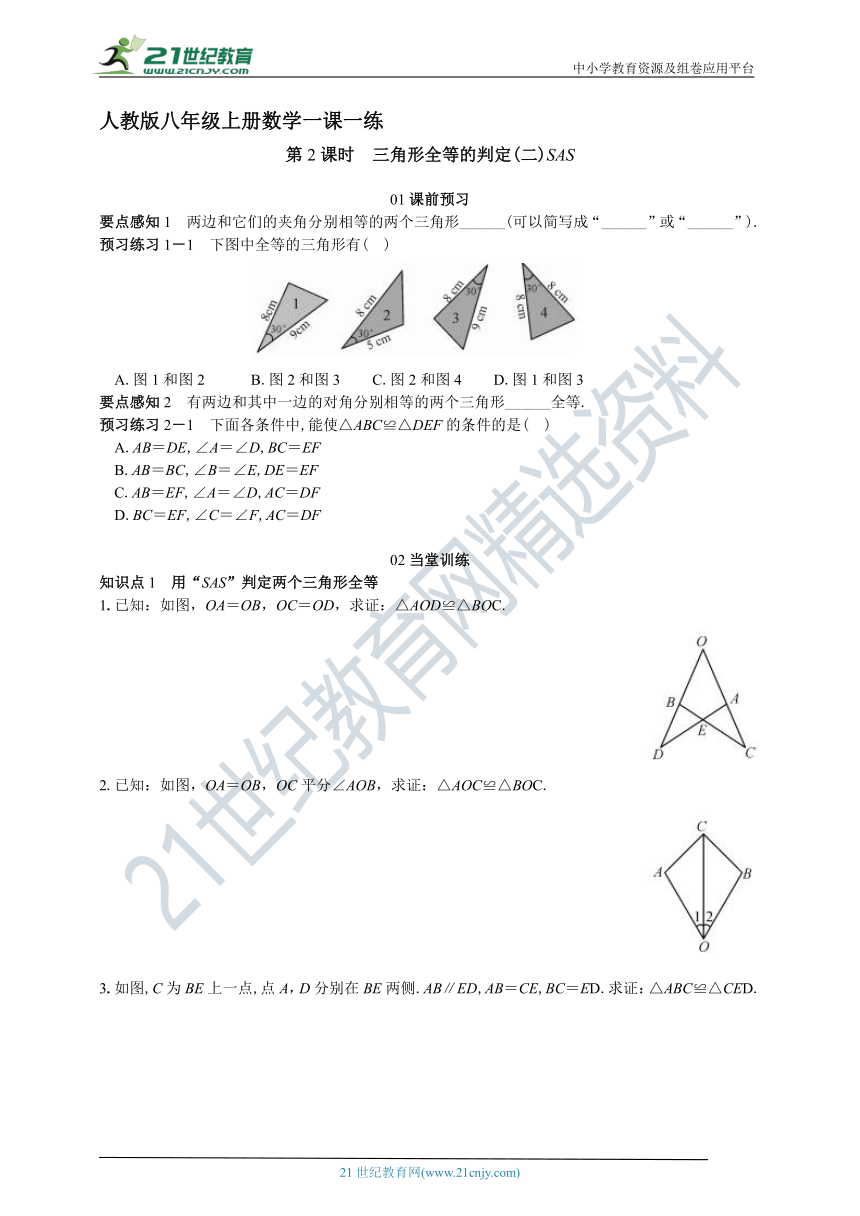 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 20:58:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学一课一练
第2课时
三角形全等的判定(二)SAS
01课前预习
要点感知1
两边和它们的夹角分别相等的两个三角形______(可以简写成“______”或“______”).
预习练习1-1
下图中全等的三角形有(
)
A.图1和图2
B.图2和图3
C.图2和图4
D.图1和图3
要点感知2
有两边和其中一边的对角分别相等的两个三角形______全等.
预习练习2-1
下面各条件中,能使△ABC≌△DEF的条件的是(
)
A.AB=DE,∠A=∠D,BC=EF
B.AB=BC,∠B=∠E,DE=EF
C.AB=EF,∠A=∠D,AC=DF
D.BC=EF,∠C=∠F,AC=DF
02当堂训练
知识点1
用“SAS”判定两个三角形全等
1.已知:如图,OA=OB,OC=OD,求证:△AOD≌△BOC.
2.已知:如图,OA=OB,OC平分∠AOB,求证:△AOC≌△BOC.
3.如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED.
知识点2
利用“SAS”判定三角形全等来证明线段或角相等
4.(武汉中考)如图,AC和BD相交于点O,OA=OC,OB=OD.求证:DC∥AB.
5.(云南中考)如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.
知识点3
利用“SAS”判定三角形全等来解决实际问题
6.如图所示,有一块三角形镜子,小明不小心将它打破成1、2两块,现需配成同样大小的一块.为了方便起见,需带上______块,其理由是______.
03课后作业
7.如图,已知AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不成立的是(
)
A.BD=CE
B.∠ABD=∠ACE
C.∠BAD=∠CAE
D.∠BAC=∠DAE
8.(陕西中考)如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
9.如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为______
.
10.如图所示,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1
km,DC=1
km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3
km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2
km,BF=0.7
km.试求建造的斜拉桥长至少有______km.
11.如图所示,AD是△ABC的高线,AD=BD,DE=DC,∠C=75°,求∠AEB的度数.
12.如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?并说明理由.
13.如图所示,A,F,C,D四点同在一直线上,AF=CD,AB∥DE,且AB=DE.求证:
(1)△ABC≌△DEF;
(2)∠CBF=∠FEC.
挑战自我
14.如图,D,E分别是△ABC的边AB,AC的中点,点F在DE的延长线上,且EF=DE,求证:
(1)BD=FC;
(2)AB∥CF.
参考答案
课前预习
要点感知1
全等
边角边
SAS
预习练习1-1
D
要点感知2
不一定
预习练习2-1
D
当堂训练
1.证明:在△AOD和△BOC中,OA=OB,∠O=∠O(公共角),OD=OC,∴△AOD≌△BOC(SAS).
2.证明:∵OC平分∠AOB,∴∠1=∠2.在△AOC和△BOC中,OA=OB,∠1=∠2(已证),
OC=OC(公共边),∴△AOC≌△BOC(SAS).
3.证明:∵AB∥ED,∴∠B=∠E.在△ABC和△CED中,AB=CE,∠B=∠E,BC=ED,∴△ABC≌△CED(SAS).
4.证明:∵在△ODC和△OBA中,OD=OB,
∠DOC=∠BOA,OC=OA,∴△ODC≌△OBA(SAS).∴∠C=∠A(或∠D=∠B).∴DC∥AB.
5.证明:在△ADB和△BAC中,AD=BC,∠DAB=∠CBA,AB=BA,∴△ADB≌△BCA(SAS).∴AC=BD.
6.1
有两边及其夹角分别相等的两个三角形全等
课后作业
7.B
8.C
9.30°
10.1.1
11.在△BDE和△ADC中,BD=AD,∠ADB=∠ADC,DE=DC,∴△BDE≌△ADC(SAS).∴∠BED=∠C=75°.∴∠AEB=105°.
12.BC∥EF.理由:∵AE=DB,∴AE+BE=DB+BE.∴AB=DE.∵AC∥DF,∴∠A=∠D.∵AC=DF,∴△ACB≌△DFE.∴∠FED=∠CBA.∴BC∥EF.
13.(1)证明:∵AB∥DE,∴∠A=∠D.又∵AF=CD,∴AF+FC=CD+FC.∴AC=DF.∵AB=DE,∴△ABC≌△DEF(SAS).(2)证明:∵△ABC≌△DEF,∴BC=EF,∠ACB=∠DFE.∵FC=CF,∴△FBC≌△CEF(SAS).∴∠CBF=∠FEC.
14.(1)证明:∵E是AC的中点,∴AE=CE.在△ADE和△CFE中,AE=CE,∠AED=∠CEF,
DE=FE,∴△ADE≌△CFE(SAS).∴AD=CF.∵D是AB的中点,∴AD=BD.∴BD=FC.(2)证明:由(1)知△ADE≌△CFE,∴∠A=∠ECF.∴AB∥CF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级上册数学一课一练
第2课时
三角形全等的判定(二)SAS
01课前预习
要点感知1
两边和它们的夹角分别相等的两个三角形______(可以简写成“______”或“______”).
预习练习1-1
下图中全等的三角形有(
)
A.图1和图2
B.图2和图3
C.图2和图4
D.图1和图3
要点感知2
有两边和其中一边的对角分别相等的两个三角形______全等.
预习练习2-1
下面各条件中,能使△ABC≌△DEF的条件的是(
)
A.AB=DE,∠A=∠D,BC=EF
B.AB=BC,∠B=∠E,DE=EF
C.AB=EF,∠A=∠D,AC=DF
D.BC=EF,∠C=∠F,AC=DF
02当堂训练
知识点1
用“SAS”判定两个三角形全等
1.已知:如图,OA=OB,OC=OD,求证:△AOD≌△BOC.
2.已知:如图,OA=OB,OC平分∠AOB,求证:△AOC≌△BOC.
3.如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED.
知识点2
利用“SAS”判定三角形全等来证明线段或角相等
4.(武汉中考)如图,AC和BD相交于点O,OA=OC,OB=OD.求证:DC∥AB.
5.(云南中考)如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.
知识点3
利用“SAS”判定三角形全等来解决实际问题
6.如图所示,有一块三角形镜子,小明不小心将它打破成1、2两块,现需配成同样大小的一块.为了方便起见,需带上______块,其理由是______.
03课后作业
7.如图,已知AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不成立的是(
)
A.BD=CE
B.∠ABD=∠ACE
C.∠BAD=∠CAE
D.∠BAC=∠DAE
8.(陕西中考)如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
9.如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为______
.
10.如图所示,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1
km,DC=1
km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3
km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2
km,BF=0.7
km.试求建造的斜拉桥长至少有______km.
11.如图所示,AD是△ABC的高线,AD=BD,DE=DC,∠C=75°,求∠AEB的度数.
12.如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?并说明理由.
13.如图所示,A,F,C,D四点同在一直线上,AF=CD,AB∥DE,且AB=DE.求证:
(1)△ABC≌△DEF;
(2)∠CBF=∠FEC.
挑战自我
14.如图,D,E分别是△ABC的边AB,AC的中点,点F在DE的延长线上,且EF=DE,求证:
(1)BD=FC;
(2)AB∥CF.
参考答案
课前预习
要点感知1
全等
边角边
SAS
预习练习1-1
D
要点感知2
不一定
预习练习2-1
D
当堂训练
1.证明:在△AOD和△BOC中,OA=OB,∠O=∠O(公共角),OD=OC,∴△AOD≌△BOC(SAS).
2.证明:∵OC平分∠AOB,∴∠1=∠2.在△AOC和△BOC中,OA=OB,∠1=∠2(已证),
OC=OC(公共边),∴△AOC≌△BOC(SAS).
3.证明:∵AB∥ED,∴∠B=∠E.在△ABC和△CED中,AB=CE,∠B=∠E,BC=ED,∴△ABC≌△CED(SAS).
4.证明:∵在△ODC和△OBA中,OD=OB,
∠DOC=∠BOA,OC=OA,∴△ODC≌△OBA(SAS).∴∠C=∠A(或∠D=∠B).∴DC∥AB.
5.证明:在△ADB和△BAC中,AD=BC,∠DAB=∠CBA,AB=BA,∴△ADB≌△BCA(SAS).∴AC=BD.
6.1
有两边及其夹角分别相等的两个三角形全等
课后作业
7.B
8.C
9.30°
10.1.1
11.在△BDE和△ADC中,BD=AD,∠ADB=∠ADC,DE=DC,∴△BDE≌△ADC(SAS).∴∠BED=∠C=75°.∴∠AEB=105°.
12.BC∥EF.理由:∵AE=DB,∴AE+BE=DB+BE.∴AB=DE.∵AC∥DF,∴∠A=∠D.∵AC=DF,∴△ACB≌△DFE.∴∠FED=∠CBA.∴BC∥EF.
13.(1)证明:∵AB∥DE,∴∠A=∠D.又∵AF=CD,∴AF+FC=CD+FC.∴AC=DF.∵AB=DE,∴△ABC≌△DEF(SAS).(2)证明:∵△ABC≌△DEF,∴BC=EF,∠ACB=∠DFE.∵FC=CF,∴△FBC≌△CEF(SAS).∴∠CBF=∠FEC.
14.(1)证明:∵E是AC的中点,∴AE=CE.在△ADE和△CFE中,AE=CE,∠AED=∠CEF,
DE=FE,∴△ADE≌△CFE(SAS).∴AD=CF.∵D是AB的中点,∴AD=BD.∴BD=FC.(2)证明:由(1)知△ADE≌△CFE,∴∠A=∠ECF.∴AB∥CF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
