人教版七年级下册数学第九章不等式与不等式组复习课件(58张)
文档属性
| 名称 | 人教版七年级下册数学第九章不等式与不等式组复习课件(58张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 21:29:03 | ||
图片预览









文档简介
(共58张PPT)
不等式与不等式组复习
一.
知识体系
1、
不等式的性质
<1>
若a>b,
则a+c>b+c
<2>若a>b,
c>0
则ac>bc
若c<0,
则ac<3>若a>b,
c>d
则a+c>b+d
同向不等式可以相加但不能相减
(
x-5y)2≥0
用不等式表示下列数量关系:
(1)2x与1的和小于零.
(2)x的一半与3的差不大于2.
(3)a是负数.
(4)a与b的和是非负数.
2x+1<0
x-3≤2
a<0
a+b
≥
0
(5)X的
与y的5倍的差的平方是一个非负数.
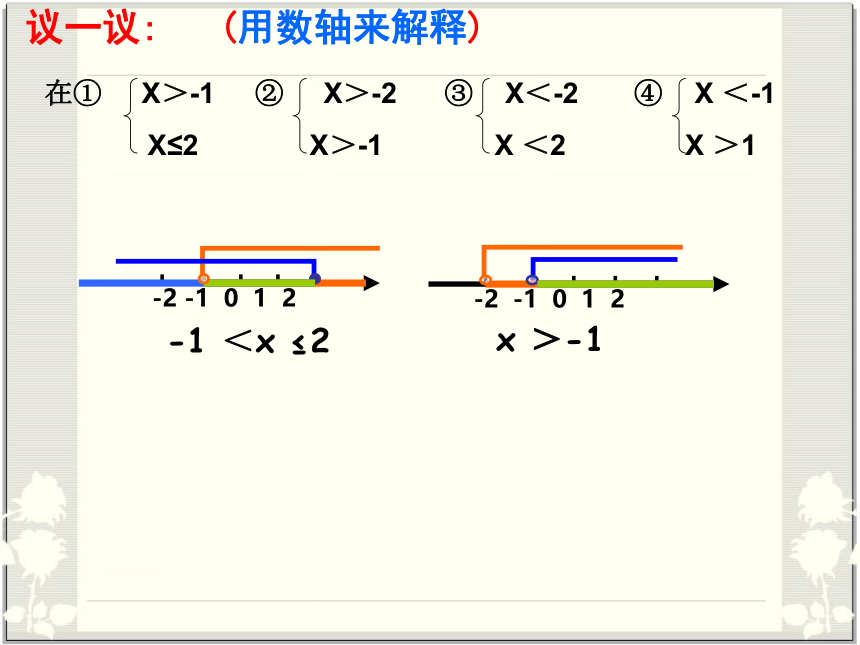
议一议:
(用数轴来解释)
-1<x≤2
议一议:
(用数轴来解释)
x
>-1
-1
<x
≤2
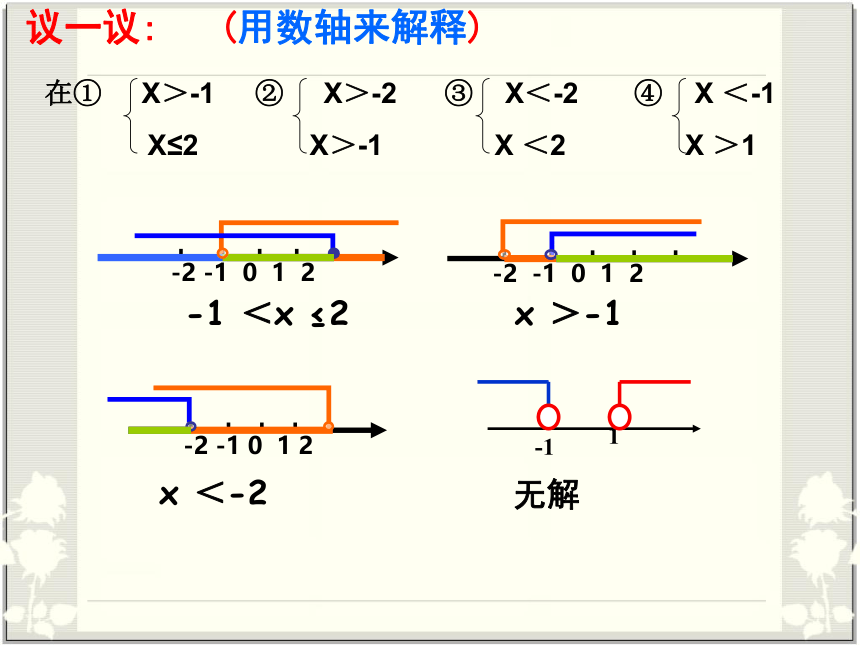
议一议:
(用数轴来解释)
x
<-2
-1
<x
≤2
x
>-1
无解
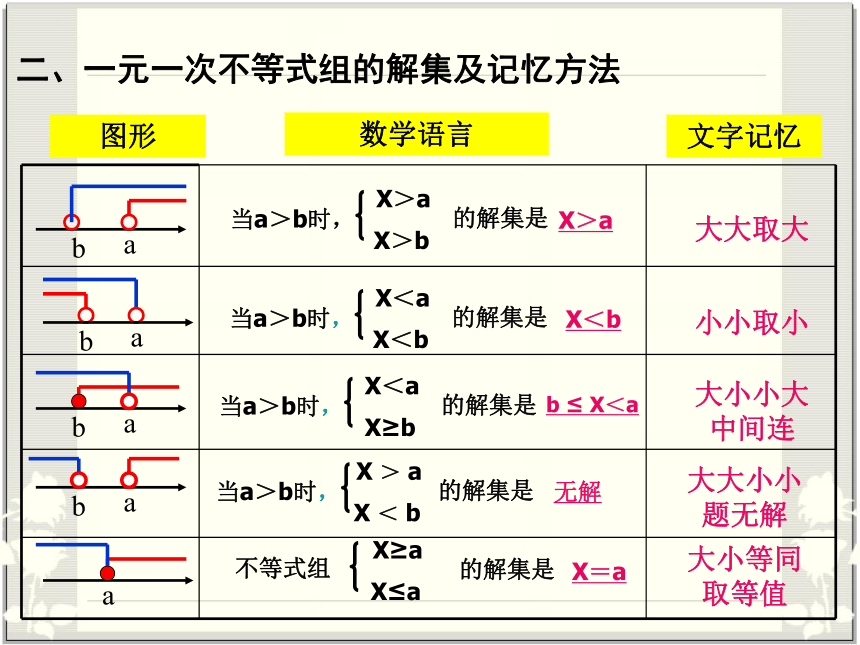
大大取大
X>a
小小取小
X<b
大小小大中间连
b
≤
X<a
大小等同取等值
X=a
大大小小题无解
无解
文字记忆
数学语言
图形
二、一元一次不等式组的解集及记忆方法
4、由不等式(m-5)x>m-5变形为x<
1,
则m需满足的条件是___________
2、若a
>b,且a、b
、
c为有理数,则ac2___bc2
5、若y=-x+7,且2≤y≤7,则x的取值范围是_____
3、已知不等式
3(x+1)
≥5x-3
正整数解是_____
二、热身训练:
1,2,3
≥
m<5
0≤x≤5
1、若a>b,则a-2___b-2,3a___3b,2-a___2-b
>
>
<
如果
m<n<0,那么下列结论中错误的是(
)
A.m-9B.-m>-n;
C.
D.
思维拓展:
C
例1:已知不等式3x-a≤0的正整数解是1,2,3,求a的范围
变式1:
不等式3x-a<0的正整数解为1,2,3,求a的范围
变式2:
不等式3x-a>0的负整数解为-1,-2,求a的范围
变式3:
不等式3x-a≥0的负整数解为-1,-2,求a的范围
解不等式:
并把解集在数轴上
表示出来。
原不等式的解集在数轴上表示如下:
2.
x
取何值时,代数式
的值:(1)小于
的值?(2)不小于
的值?
3.?己知
(1)当m为何值
时,
y
≥
0
?
(2)当m为何值时,y
<
-2
4.?当k取何值时,方程
的解
是正数。
5.
求同时满足不等式6x-2≥3x-4
和
的整数x
.
6.?要使3个连续奇数之和不小于100.
那么3个奇数
中,最小的奇数,应当不小于什么数?
7.?
解不等式组
并把它的解集
在数轴上表示出来。
8.
己知
求a
的取值范围。
9.??
解不等式
10.
解不等式组:
11.若
,求m的取值范围。
12.不等式x-8>3x-5
的最大整数解是(
)
13.x
取何值时,代数式
的值不小于
的值。
14.求不等式
的解集。
15.写出绝对值不大于是3
的所有整数。
16.
若
中
y
为非负数,
求k值。
17.当k为何值时,关于x的方程4(x+k)=x+5的解
是(1)0
;(2)
小于
–
3
.
18.把一个2位数的个位数字与十位数字对调,所
得的2位数比原2位数小18,
且知个位数字与十
位数字之和为6,求原来的2位数。
19.关于x的方程2+k(x-1)=x(k-2)+4x
的解若是
正数,那么k的值为(
)。
20.满足不等式5-3x>-1的正整数值,是方程
4(x-2)-[5(1-2x)-4(5x-1)]=a
的解,则a的值
是多少
?
21.如果a+b<0
,则不等式(a+b)x>a+b的解集
是(
)。
22.不等式
的非负整数解是(
)
23.方程组
的解为
则a的
取值范围是(
)。
24.解关于x的方程3x-(2a-3)=4x+(3a+6)
,
当解x
为负数时,求a
的值。
25.方程x+2k=4(x+k)+1有正数解时,k的取值
范围是(
)。
26.不等式
的解集是x>2
,求a的值
27.关于x
的不等式
的解都是不等式
的解,则a的取值范围为(
)
你能找出下列语句中的不等关系吗?
(1)小明家五月份的电费不超过50元;小华家五月份的电费不足100元;
小明家五月份电费≤50
小华家五月份的电费<100
隐含:
小华家五月份电费≥0
你能找出下列语句中的不等关系吗?
(2)小红星期天去逛街时带的钱不足200元,她花X元给自己买了一条裙子;
小红带的钱数<200
0<X<200
隐含:
你能找出下列语句中的不等关系吗?
(3)某工厂有原料200吨,现要生产甲、乙两种产品各X件,已知每件甲产品需用原料10吨,每件乙产品需用原料8吨。
甲产品用的原料+乙产品用的原料≤总原料
即:
10X+8X≤200
七年级某班元旦联欢时要分糖块,如果每人分3块,那么多8块,如果前面每人分5块,那么最后一位同学得到的糖少于3块。
不等关系
最后一位同学分到的糖<3
最后一位同学分到的糖≥0
隐含
问题1:
某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A产品需用甲种原料9千克,乙种原料3千克,出售后可获利700元;生产一件B产品需用甲种原料4千克,乙种原料10千克,出售后可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请设计出来.
(2)上面方案中哪种方案的获利最大,最大利润是多少?
问题3:
我校要举行文艺比赛,将评出一等奖5名,二等奖10名,三等奖15名,学校决定给获奖同学发奖品,同一等次的奖品相同,并且只能从下表所列物品中选取一件:
学校规定获奖等次越高,奖品单价越高,如果要求一等奖的奖品单价是二等奖奖品单价的5倍,二等奖的奖品单价是三等奖奖品单价的4倍,在总费用不超过1000元的前提下,有几种购买方案?花费最多的一种方案需要多少钱?
品名
小提琴
运动服
笛子
舞鞋
口琴
相册
笔记本
钢笔
单价(元)
120
80
24
22
16
6
5
4
题中的不等关系:
一等奖奖品费用
+
二等
+
三等≤1000
一等奖奖品单价≤120,
三等奖奖品单价≥4
解:
设三等奖的奖品单价为X元,二等奖奖品单价为4X元,一等奖奖品单价为20X元,则:
5×20X+10×4X+15X≤1000
20X
≤120
X
≥4
解得:4≤X≤6
解:
设三等奖的奖品单价为X元,二等奖奖品单价为4X元,一等奖奖品单价为20X元,则:
解得:4≤X≤6
所以,有两种购买方案:
方案1:三等奖奖品单价6元,二等奖奖品单价24元,一等奖奖品单价120元;
方案2:三等奖奖品单价4元,二等奖奖品单价16元,一等奖奖品单价80元.
花费最多需:5×120+10×24
+15×6=930(元)
问题2:祥云化工厂2004年12月在制定2005年某种化工产品的生产计划时,提供了下列数据:
(1)生产该产品的工人数不能超过200人;
(2)每个工人全年工作时数是2100小时;
(3)预计2005年该产品至少可以销售80000袋;(4)每生产一袋需要一个工人做4小时;
(5)每袋需要原料20千克;
(6)现在库存原料800吨,本月还需用200吨,2005年还可以补充1200吨.
试根据以上数据确定2005年该产品的生产计划.
1、若|3a-5|=5-3a,则a______.
不等式与绝对值,函数等知识结合的应用
2、已知一次函数y=(3k-6)x+1,y随x的增大而增大,则k的取值范围是______.
3、点P(-2a+1,
5)在第二象限,则a_____.
如果关于x的方程3x+a=x+4的解是非负数,求a的取值范围。
X是非负数
不等式与方程结合的应用
例、3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
〔解答〕设每个小组原来每天生产x件产品,则有
由不等式①得
由②得
又x为整数,所以x=16,即每个小组原来每天生产16件产品.
边学边练1、某中学为七年级寄宿学生安排宿舍,如果每间4人,那么有20人无法安排,如果每间8人,那么有一间不空也不满,求宿舍间数和寄宿学生人数。
解:设宿舍有x间,学生人数是(4x+20)人
0<8x-(4x+20)<8
由①得:x>5
由②得:x<7
所以:x=6
问题3
用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不超过1500吨,那么大约需要多少时间才能将污水抽完?
提示:
问题中包含着
个应用条件;
若设需要x
分钟才能将污水抽完,则条件一是什么?
第二个条件是
。
两个
总抽水量30x吨应大于或等于1200吨
总抽水量30x应小于或等于1500吨
解:
设需要x分钟才能将污水抽完,那么总的抽水量为30x吨。由题意,积存的污水在1200吨到1500吨之间,应有
1200≤30x≤1500
上式实际上包括了两个不等式
30≥1200
和
30x≤1500
一元一次不等式组的概念:
它说明了在这个实际问题中,未知量x应同时满足这两个条件。我们把这两个一元一次不等式合在一起,就得到一个一元一次不等式组:
分别解得
在数轴上表示
(分别求出①、②)
分别求这两个不等式的解集
概括
几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集。
解一元一次不等式组,通常可以先分别求出不等式组中每一个不等式的解集,再求出它们的公共部分。利用数轴可以直观地帮助我们求出不等式组的解集。
完成下列表格
x
>
a
x
<
b
b<
a
无解
1.
同大取大,
2.同小取小;
3.大小小大中间找,
4.大大小小解不了。
不等式与不等式组复习
一.
知识体系
1、
不等式的性质
<1>
若a>b,
则a+c>b+c
<2>若a>b,
c>0
则ac>bc
若c<0,
则ac
c>d
则a+c>b+d
同向不等式可以相加但不能相减
(
x-5y)2≥0
用不等式表示下列数量关系:
(1)2x与1的和小于零.
(2)x的一半与3的差不大于2.
(3)a是负数.
(4)a与b的和是非负数.
2x+1<0
x-3≤2
a<0
a+b
≥
0
(5)X的
与y的5倍的差的平方是一个非负数.
议一议:
(用数轴来解释)
-1<x≤2
议一议:
(用数轴来解释)
x
>-1
-1
<x
≤2
议一议:
(用数轴来解释)
x
<-2
-1
<x
≤2
x
>-1
无解
大大取大
X>a
小小取小
X<b
大小小大中间连
b
≤
X<a
大小等同取等值
X=a
大大小小题无解
无解
文字记忆
数学语言
图形
二、一元一次不等式组的解集及记忆方法
4、由不等式(m-5)x>m-5变形为x<
1,
则m需满足的条件是___________
2、若a
>b,且a、b
、
c为有理数,则ac2___bc2
5、若y=-x+7,且2≤y≤7,则x的取值范围是_____
3、已知不等式
3(x+1)
≥5x-3
正整数解是_____
二、热身训练:
1,2,3
≥
m<5
0≤x≤5
1、若a>b,则a-2___b-2,3a___3b,2-a___2-b
>
>
<
如果
m<n<0,那么下列结论中错误的是(
)
A.m-9
C.
D.
思维拓展:
C
例1:已知不等式3x-a≤0的正整数解是1,2,3,求a的范围
变式1:
不等式3x-a<0的正整数解为1,2,3,求a的范围
变式2:
不等式3x-a>0的负整数解为-1,-2,求a的范围
变式3:
不等式3x-a≥0的负整数解为-1,-2,求a的范围
解不等式:
并把解集在数轴上
表示出来。
原不等式的解集在数轴上表示如下:
2.
x
取何值时,代数式
的值:(1)小于
的值?(2)不小于
的值?
3.?己知
(1)当m为何值
时,
y
≥
0
?
(2)当m为何值时,y
<
-2
4.?当k取何值时,方程
的解
是正数。
5.
求同时满足不等式6x-2≥3x-4
和
的整数x
.
6.?要使3个连续奇数之和不小于100.
那么3个奇数
中,最小的奇数,应当不小于什么数?
7.?
解不等式组
并把它的解集
在数轴上表示出来。
8.
己知
求a
的取值范围。
9.??
解不等式
10.
解不等式组:
11.若
,求m的取值范围。
12.不等式x-8>3x-5
的最大整数解是(
)
13.x
取何值时,代数式
的值不小于
的值。
14.求不等式
的解集。
15.写出绝对值不大于是3
的所有整数。
16.
若
中
y
为非负数,
求k值。
17.当k为何值时,关于x的方程4(x+k)=x+5的解
是(1)0
;(2)
小于
–
3
.
18.把一个2位数的个位数字与十位数字对调,所
得的2位数比原2位数小18,
且知个位数字与十
位数字之和为6,求原来的2位数。
19.关于x的方程2+k(x-1)=x(k-2)+4x
的解若是
正数,那么k的值为(
)。
20.满足不等式5-3x>-1的正整数值,是方程
4(x-2)-[5(1-2x)-4(5x-1)]=a
的解,则a的值
是多少
?
21.如果a+b<0
,则不等式(a+b)x>a+b的解集
是(
)。
22.不等式
的非负整数解是(
)
23.方程组
的解为
则a的
取值范围是(
)。
24.解关于x的方程3x-(2a-3)=4x+(3a+6)
,
当解x
为负数时,求a
的值。
25.方程x+2k=4(x+k)+1有正数解时,k的取值
范围是(
)。
26.不等式
的解集是x>2
,求a的值
27.关于x
的不等式
的解都是不等式
的解,则a的取值范围为(
)
你能找出下列语句中的不等关系吗?
(1)小明家五月份的电费不超过50元;小华家五月份的电费不足100元;
小明家五月份电费≤50
小华家五月份的电费<100
隐含:
小华家五月份电费≥0
你能找出下列语句中的不等关系吗?
(2)小红星期天去逛街时带的钱不足200元,她花X元给自己买了一条裙子;
小红带的钱数<200
0<X<200
隐含:
你能找出下列语句中的不等关系吗?
(3)某工厂有原料200吨,现要生产甲、乙两种产品各X件,已知每件甲产品需用原料10吨,每件乙产品需用原料8吨。
甲产品用的原料+乙产品用的原料≤总原料
即:
10X+8X≤200
七年级某班元旦联欢时要分糖块,如果每人分3块,那么多8块,如果前面每人分5块,那么最后一位同学得到的糖少于3块。
不等关系
最后一位同学分到的糖<3
最后一位同学分到的糖≥0
隐含
问题1:
某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A产品需用甲种原料9千克,乙种原料3千克,出售后可获利700元;生产一件B产品需用甲种原料4千克,乙种原料10千克,出售后可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请设计出来.
(2)上面方案中哪种方案的获利最大,最大利润是多少?
问题3:
我校要举行文艺比赛,将评出一等奖5名,二等奖10名,三等奖15名,学校决定给获奖同学发奖品,同一等次的奖品相同,并且只能从下表所列物品中选取一件:
学校规定获奖等次越高,奖品单价越高,如果要求一等奖的奖品单价是二等奖奖品单价的5倍,二等奖的奖品单价是三等奖奖品单价的4倍,在总费用不超过1000元的前提下,有几种购买方案?花费最多的一种方案需要多少钱?
品名
小提琴
运动服
笛子
舞鞋
口琴
相册
笔记本
钢笔
单价(元)
120
80
24
22
16
6
5
4
题中的不等关系:
一等奖奖品费用
+
二等
+
三等≤1000
一等奖奖品单价≤120,
三等奖奖品单价≥4
解:
设三等奖的奖品单价为X元,二等奖奖品单价为4X元,一等奖奖品单价为20X元,则:
5×20X+10×4X+15X≤1000
20X
≤120
X
≥4
解得:4≤X≤6
解:
设三等奖的奖品单价为X元,二等奖奖品单价为4X元,一等奖奖品单价为20X元,则:
解得:4≤X≤6
所以,有两种购买方案:
方案1:三等奖奖品单价6元,二等奖奖品单价24元,一等奖奖品单价120元;
方案2:三等奖奖品单价4元,二等奖奖品单价16元,一等奖奖品单价80元.
花费最多需:5×120+10×24
+15×6=930(元)
问题2:祥云化工厂2004年12月在制定2005年某种化工产品的生产计划时,提供了下列数据:
(1)生产该产品的工人数不能超过200人;
(2)每个工人全年工作时数是2100小时;
(3)预计2005年该产品至少可以销售80000袋;(4)每生产一袋需要一个工人做4小时;
(5)每袋需要原料20千克;
(6)现在库存原料800吨,本月还需用200吨,2005年还可以补充1200吨.
试根据以上数据确定2005年该产品的生产计划.
1、若|3a-5|=5-3a,则a______.
不等式与绝对值,函数等知识结合的应用
2、已知一次函数y=(3k-6)x+1,y随x的增大而增大,则k的取值范围是______.
3、点P(-2a+1,
5)在第二象限,则a_____.
如果关于x的方程3x+a=x+4的解是非负数,求a的取值范围。
X是非负数
不等式与方程结合的应用
例、3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
〔解答〕设每个小组原来每天生产x件产品,则有
由不等式①得
由②得
又x为整数,所以x=16,即每个小组原来每天生产16件产品.
边学边练1、某中学为七年级寄宿学生安排宿舍,如果每间4人,那么有20人无法安排,如果每间8人,那么有一间不空也不满,求宿舍间数和寄宿学生人数。
解:设宿舍有x间,学生人数是(4x+20)人
0<8x-(4x+20)<8
由①得:x>5
由②得:x<7
所以:x=6
问题3
用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不超过1500吨,那么大约需要多少时间才能将污水抽完?
提示:
问题中包含着
个应用条件;
若设需要x
分钟才能将污水抽完,则条件一是什么?
第二个条件是
。
两个
总抽水量30x吨应大于或等于1200吨
总抽水量30x应小于或等于1500吨
解:
设需要x分钟才能将污水抽完,那么总的抽水量为30x吨。由题意,积存的污水在1200吨到1500吨之间,应有
1200≤30x≤1500
上式实际上包括了两个不等式
30≥1200
和
30x≤1500
一元一次不等式组的概念:
它说明了在这个实际问题中,未知量x应同时满足这两个条件。我们把这两个一元一次不等式合在一起,就得到一个一元一次不等式组:
分别解得
在数轴上表示
(分别求出①、②)
分别求这两个不等式的解集
概括
几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集。
解一元一次不等式组,通常可以先分别求出不等式组中每一个不等式的解集,再求出它们的公共部分。利用数轴可以直观地帮助我们求出不等式组的解集。
完成下列表格
x
>
a
x
<
b
b
a
无解
1.
同大取大,
2.同小取小;
3.大小小大中间找,
4.大大小小解不了。
