人教版八年级下册数学17.1 勾股定理的应用课件 (共19张PPT)
文档属性
| 名称 | 人教版八年级下册数学17.1 勾股定理的应用课件 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 729.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
勾股定理的应用
勾股定理
:直角三角形两直角边的平方和等于斜边的平方
1、勾股定理的内容是什么?
2、圆柱的侧面展开图是
。
3、展开图的长相当于圆柱的_________,
宽相当于圆柱的
。
长方形
底面周长
高
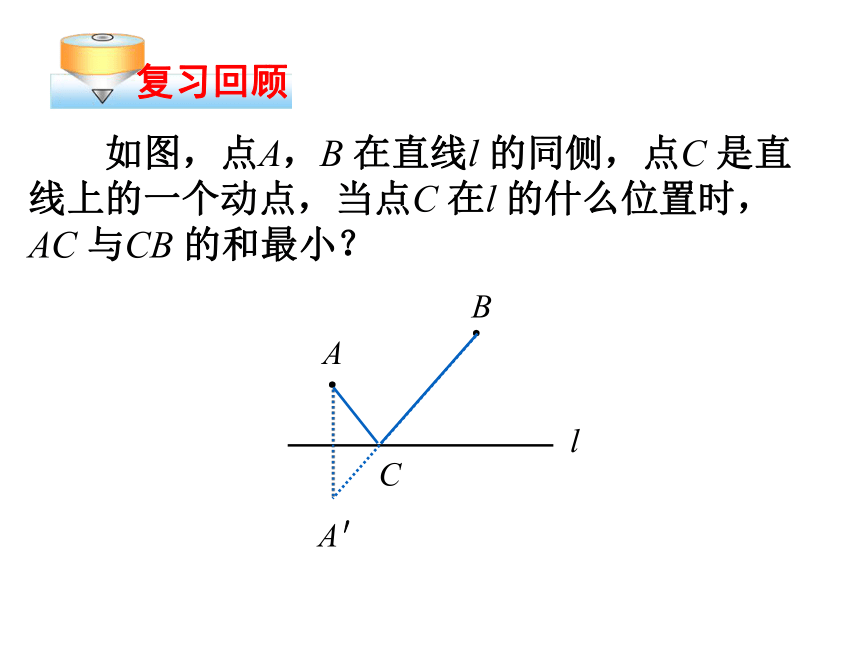
如图,点A,B
在直线l
的同侧,点C
是直线上的一个动点,当点C
在l
的什么位置时,AC
与CB
的和最小?
A′
C
B
A
勾股定理的应用
求解几何体的最短路径
“小黑当家”
有一只叫小黑的蚂蚁,有一天,妈妈出门前,给小黑准备了好吃的食物,可是放在了不同的地方,聪明的小黑能找到这些食物吗?
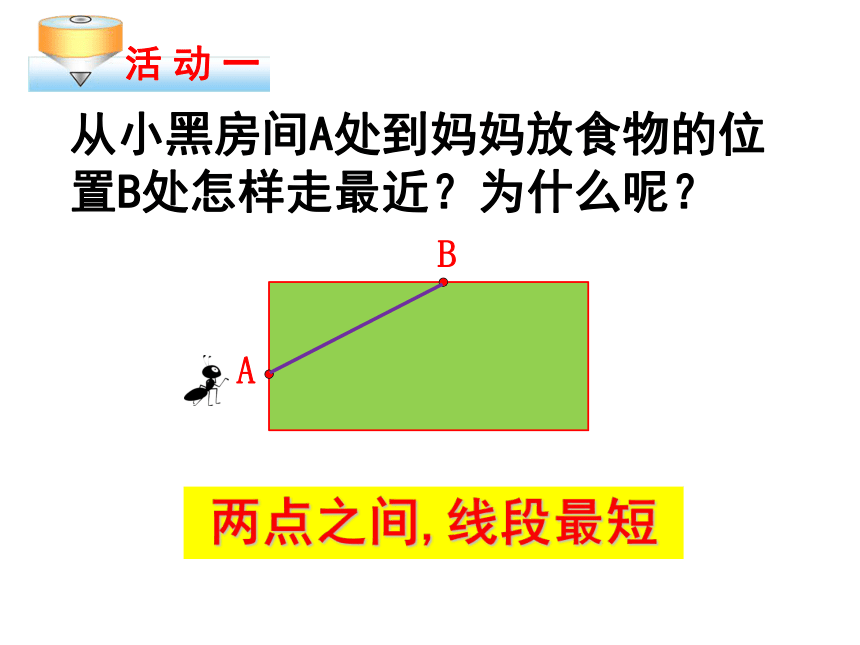
两点之间,线段最短
从小黑房间A处到妈妈放食物的位置B处怎样走最近?为什么呢?
A
B
B
在一个圆柱形小凳子上,若妈妈把食物放在点B处,小黑在A处闻到了食物的味道,于是它想从A处沿圆柱形小凳子表面爬行到B处,你们想一想,小黑怎么走最近?
A
以小组为单位,探究小黑爬行的最短路线
B
A
B
A
C
O
h
如何计算AB?
A
B
C
侧面展开图
A
B
如图,有一个高为15cm,底面周长为16cm的圆柱,在圆柱下底面的A点小黑想吃到圆柱上底面上与A点相对的B点处的食物,问小黑沿着侧面需要爬行的最短路程为多少厘米?
求立体图形中最短路径问题的方法
1、展
2、找
3、连
4、算
将立体图形展开为平面图形
找到相关点的位置
连接相关点,构造直角三角形
根据勾股定理求解
A
A
在一个高为15cm,底面周长为16cm的圆柱形杯子上,若有一滴蜂蜜在杯外壁离杯口9cm的点B处,小黑在杯外壁点A处爬向B处,你们想一想,小黑沿圆柱侧面爬行的最短路程是多少?
1.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则小黑从外壁A处到达内壁B处的最短距离为多少?
C
通过这节课的学习
谈谈你的收获
勾股定理的应用
勾股定理
:直角三角形两直角边的平方和等于斜边的平方
1、勾股定理的内容是什么?
2、圆柱的侧面展开图是
。
3、展开图的长相当于圆柱的_________,
宽相当于圆柱的
。
长方形
底面周长
高
如图,点A,B
在直线l
的同侧,点C
是直线上的一个动点,当点C
在l
的什么位置时,AC
与CB
的和最小?
A′
C
B
A
勾股定理的应用
求解几何体的最短路径
“小黑当家”
有一只叫小黑的蚂蚁,有一天,妈妈出门前,给小黑准备了好吃的食物,可是放在了不同的地方,聪明的小黑能找到这些食物吗?
两点之间,线段最短
从小黑房间A处到妈妈放食物的位置B处怎样走最近?为什么呢?
A
B
B
在一个圆柱形小凳子上,若妈妈把食物放在点B处,小黑在A处闻到了食物的味道,于是它想从A处沿圆柱形小凳子表面爬行到B处,你们想一想,小黑怎么走最近?
A
以小组为单位,探究小黑爬行的最短路线
B
A
B
A
C
O
h
如何计算AB?
A
B
C
侧面展开图
A
B
如图,有一个高为15cm,底面周长为16cm的圆柱,在圆柱下底面的A点小黑想吃到圆柱上底面上与A点相对的B点处的食物,问小黑沿着侧面需要爬行的最短路程为多少厘米?
求立体图形中最短路径问题的方法
1、展
2、找
3、连
4、算
将立体图形展开为平面图形
找到相关点的位置
连接相关点,构造直角三角形
根据勾股定理求解
A
A
在一个高为15cm,底面周长为16cm的圆柱形杯子上,若有一滴蜂蜜在杯外壁离杯口9cm的点B处,小黑在杯外壁点A处爬向B处,你们想一想,小黑沿圆柱侧面爬行的最短路程是多少?
1.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则小黑从外壁A处到达内壁B处的最短距离为多少?
C
通过这节课的学习
谈谈你的收获
