人教版八年级下册数学18.1.2平行四边形判定定理的简单应用课件 (共17张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.2平行四边形判定定理的简单应用课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 10:46:13 | ||
图片预览




文档简介
(共17张PPT)
平行四边形判定的简单应用
平行四边形的性质:
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对角线互相平分
平行四边形的判定:
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
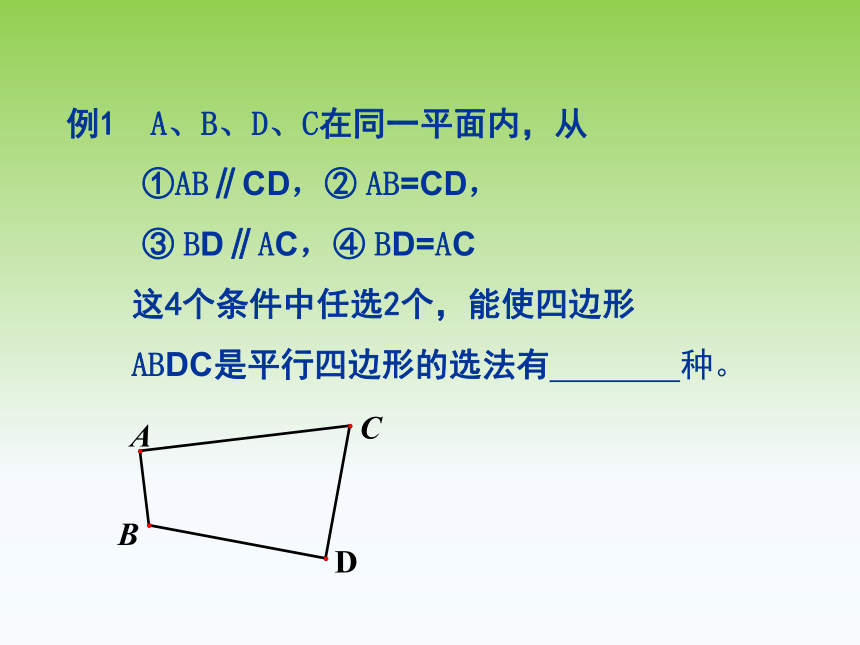
例1
A、B、D、C在同一平面内,从
①AB∥CD,②
AB=CD,
③
BD∥AC,④
BD=AC
这4个条件中任选2个,能使四边形
ABDC是平行四边形的选法有
种。
例题新授
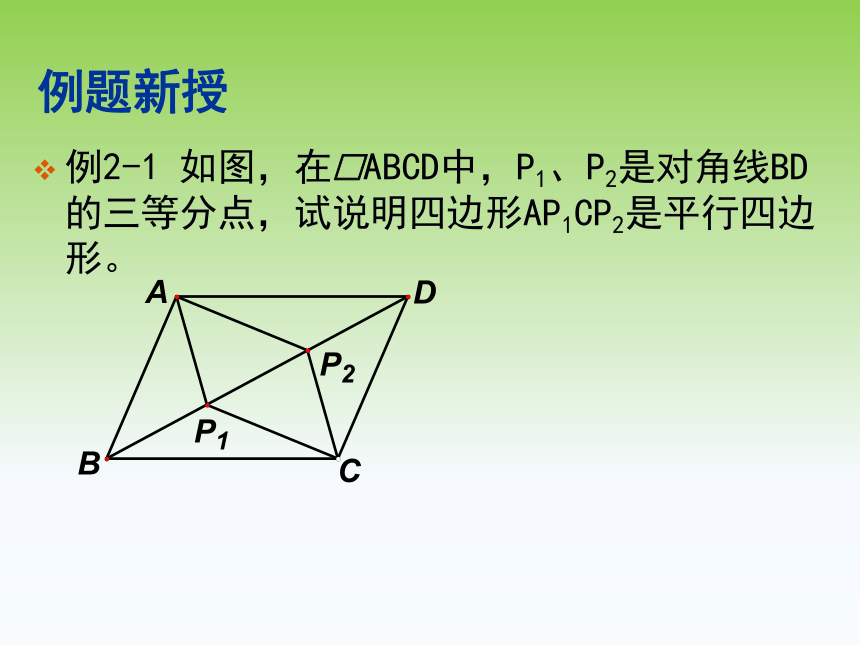
例2-1
如图,在□ABCD中,P1、P2是对角线BD的三等分点,试说明四边形AP1CP2是平行四边形。
例题新授
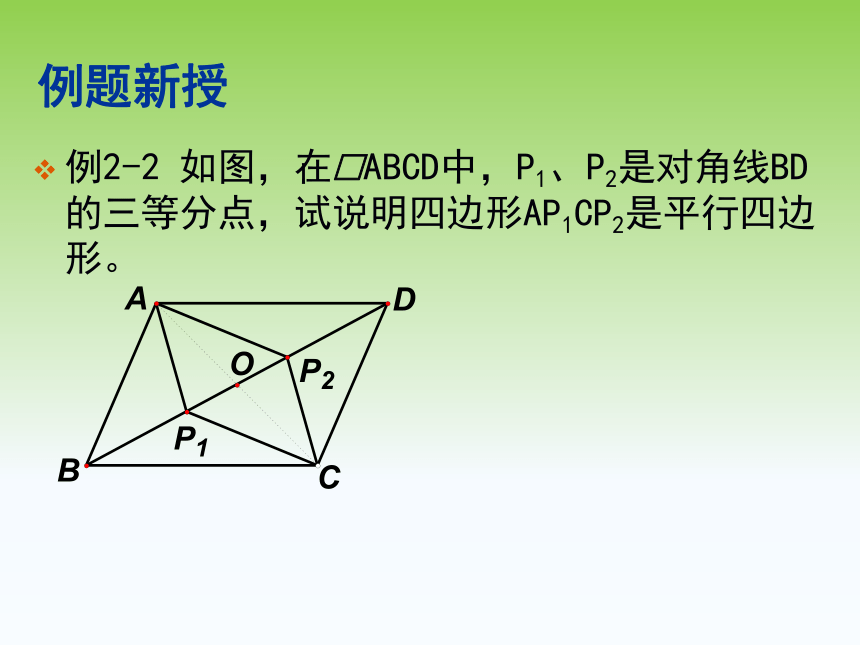
例2-2
如图,在□ABCD中,P1、P2是对角线BD的三等分点,试说明四边形AP1CP2是平行四边形。
方法归纳
平行四边形的判定必须根据题目的条件,合理筛选判定的方法。如本题涉及对角线问题,是较为典型的“用平行四边形证平行四边形”,通常采用对角线的有关知识来解决问题。
例3
如图,过□ABCD
的四个顶点,分别向两条对角线引垂线,垂足分别为E、H、G、F,四边形EFGH
是平行四边形吗?为什么?
方法归纳
要学会从复杂的图形中分离出基本图形,化繁为简,逐步培养自己透过现象看本质的能力。
试一试:如图,已知M是RtΔABC斜边BC的中点,
P、Q分别在AB、AC上,且PM⊥QM,
求证:PQ2
=PB2
+QC2
。
如图,已知M是RtΔABC斜边BC的中点,
P、Q分别在AB、AC上,且PM⊥QM,
求证:PQ2
=PB2
+QC2
。
方法归纳
延长三角形过一边中点的线段至一倍,构成平行四边形,可以将不相邻的三条边转化到同一三角形中。这也是用动态的观念解决几何问题的常用方法。
练习1:如图,四边形ABCD是平行四边形,BD⊥AD,AD=8,AB=10,求OB的长。
及时巩固
练习2:如图,□ABCD
中,E在AC上,AE=2EC,
F在AB上,BF=2AF,如果ΔBEF的面积为2cm2,
求□ABCD
的面积。
提示:
面积变换在面积问题中,求线段的比的问题时常用到。面积变换具有下面一些性质:
⑴等底(或同底)等高(或同高)的两个三角形(或平行四边形)面积相等;⑵等底(或等高)的两个三角形(或平行四边形)的面积的比等于对应高(或底)的比。
祝同学们学习进步!
再见
平行四边形判定的简单应用
平行四边形的性质:
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对角线互相平分
平行四边形的判定:
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
例1
A、B、D、C在同一平面内,从
①AB∥CD,②
AB=CD,
③
BD∥AC,④
BD=AC
这4个条件中任选2个,能使四边形
ABDC是平行四边形的选法有
种。
例题新授
例2-1
如图,在□ABCD中,P1、P2是对角线BD的三等分点,试说明四边形AP1CP2是平行四边形。
例题新授
例2-2
如图,在□ABCD中,P1、P2是对角线BD的三等分点,试说明四边形AP1CP2是平行四边形。
方法归纳
平行四边形的判定必须根据题目的条件,合理筛选判定的方法。如本题涉及对角线问题,是较为典型的“用平行四边形证平行四边形”,通常采用对角线的有关知识来解决问题。
例3
如图,过□ABCD
的四个顶点,分别向两条对角线引垂线,垂足分别为E、H、G、F,四边形EFGH
是平行四边形吗?为什么?
方法归纳
要学会从复杂的图形中分离出基本图形,化繁为简,逐步培养自己透过现象看本质的能力。
试一试:如图,已知M是RtΔABC斜边BC的中点,
P、Q分别在AB、AC上,且PM⊥QM,
求证:PQ2
=PB2
+QC2
。
如图,已知M是RtΔABC斜边BC的中点,
P、Q分别在AB、AC上,且PM⊥QM,
求证:PQ2
=PB2
+QC2
。
方法归纳
延长三角形过一边中点的线段至一倍,构成平行四边形,可以将不相邻的三条边转化到同一三角形中。这也是用动态的观念解决几何问题的常用方法。
练习1:如图,四边形ABCD是平行四边形,BD⊥AD,AD=8,AB=10,求OB的长。
及时巩固
练习2:如图,□ABCD
中,E在AC上,AE=2EC,
F在AB上,BF=2AF,如果ΔBEF的面积为2cm2,
求□ABCD
的面积。
提示:
面积变换在面积问题中,求线段的比的问题时常用到。面积变换具有下面一些性质:
⑴等底(或同底)等高(或同高)的两个三角形(或平行四边形)面积相等;⑵等底(或等高)的两个三角形(或平行四边形)的面积的比等于对应高(或底)的比。
祝同学们学习进步!
再见
