人教版数学八年级下册:19.2.1 正比例函数 (第2课时) 课件 (共18张PPT)
文档属性
| 名称 | 人教版数学八年级下册:19.2.1 正比例函数 (第2课时) 课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 07:36:46 | ||
图片预览


文档简介
(共18张PPT)
19.2
一次函数
19.2.1
正比例函数
(第2课时)
1.正比例函数的定义
一般地,形如
y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
2.画函数图象的步骤
列表、描点、连线
-4
-2
0
2
4
y=2x
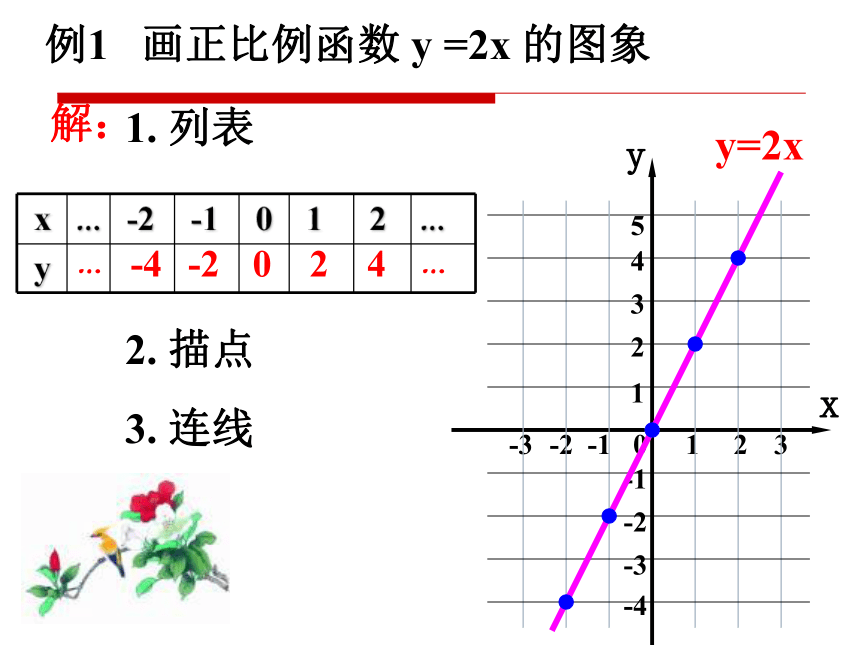
例1
画正比例函数
y
=2x
的图象
解:
1.
列表
2.
描点
3.
连线
…
…
x
…
-2
-1
0
1
2
…
y
y=2x
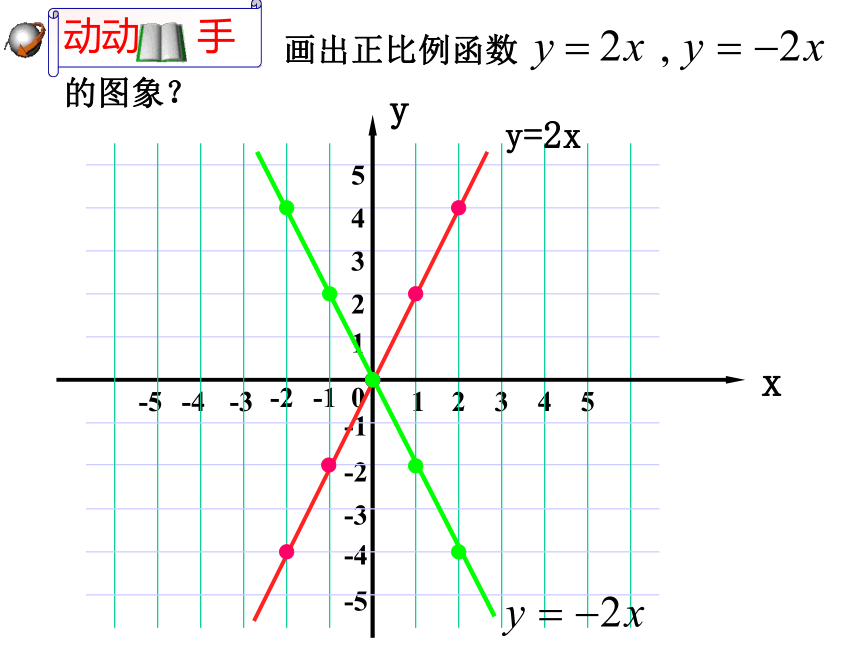
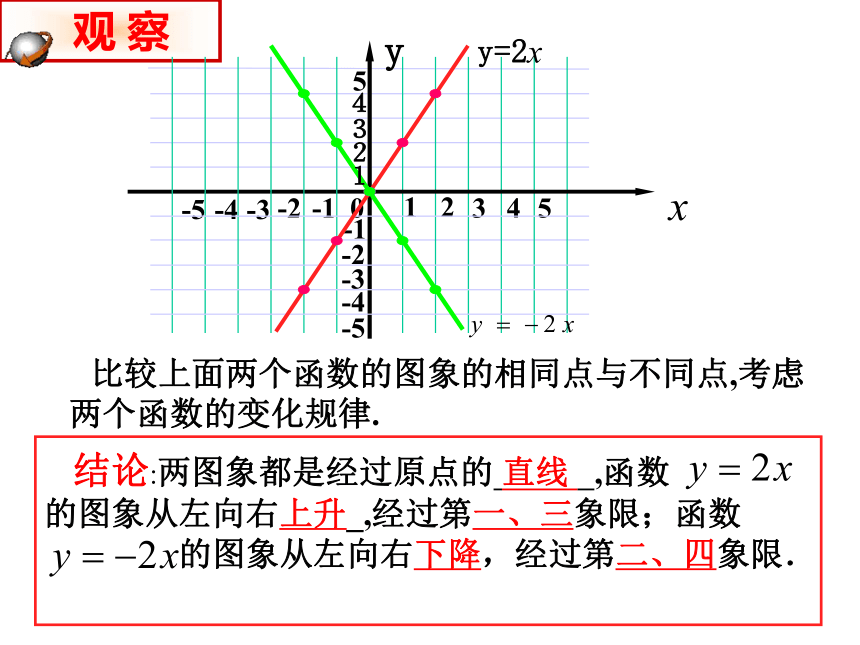
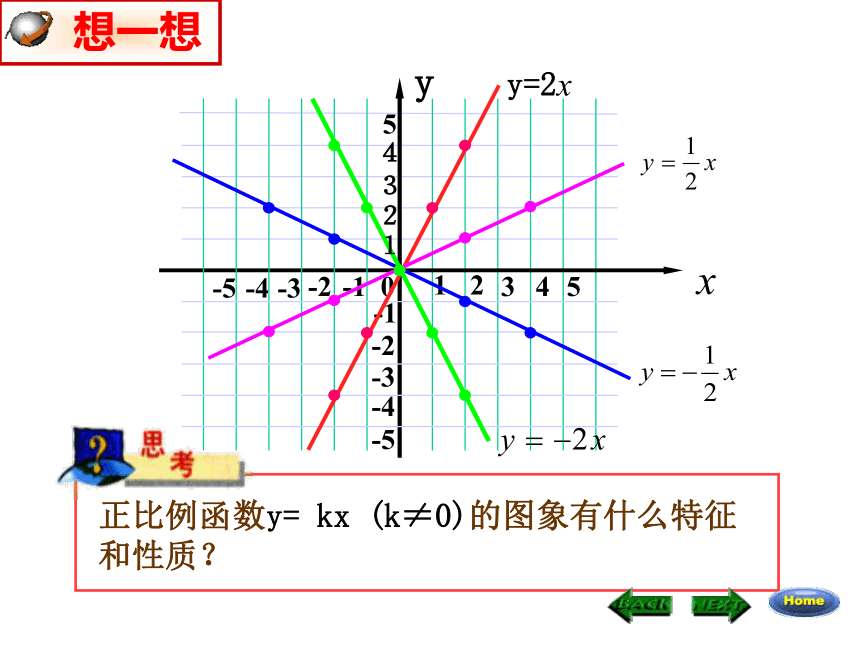
比较上面两个函数的图象的相同点与不同点,考虑
两个函数的变化规律.
一般地,正比例函数y=kx(k是常数,k≠0)的图象
直线y=kx经过第一、三象限,
直线y=kx经过第二、四象限,
我们称它为直线y=kx.
正比例函数图象的特征及性质:
是一条经过原点的直线,
当k
>0时,
当k
<0时,
从左向右上升,
即随着x的增大y也增大;
从左向右下降,
即随着x的增大y反而减小.
x
y
0
1
1
当
|k|
越大时,图像越靠近y轴
当
|k|
相等时,图像关于坐标轴对称
补充性质:
如图,三个正比例函数的图象分别对应的解析式是
①y=ax②
y=bx
③
y=cx,则a、b、c的大小关系是(
)
A.a>b>c
B.c>b>a
C.b>a>c
D.b>c>a
x
y
①
②
③
C
1
k
1
k
y=
kx
(k>0)
正比例函数y=
kx
(k≠0)
的图象是经过原点(0,0)和点(1,k)的一条直线。
解:选取两点(0,0)
,
(1,3)
1.画函数
y
=
3x
的图象
y=3x
过这两点画直线,
就是函数y=
3x
的图象
过这两点画直线,
B
二、四
0
-3
减小
1.
正比例函数y=(m-1)x的图象经过一、三象限,
A.
m=1
B.
m>1
C.
m<1
D.
m≥1
3.
函数y=-3x的图象在第
象限内,经过点
2.
正比例函数y=(3-k)
x,如果随着x的增大y反而减
小,则k的取值范围是
______.
k>3
4.
函数y=
x的图象在第
象限内,经过点
(0,
)与点(1,
),y随x的增大而
.
(0,
)与点(1,
),y随x的增大而
.
三、一
0
增大
则m的取值范围是(
)
5.
如果正比例函数y=(8-2a)x的图像经过二、四象限,求a的取值范围。
解:
∴比例系数k=8-2a<0
∴a>4
∵该函数图像经过二、四象限
问:如果正比例函数y=(8-2a)x,y的值随x的值增大而减少,求a的取值范围。
a>4
6.已知正比例函数y=(m+1)xm2
,它的图象经过第几象限?
解:
比例系数k=m+1=2>0
∵该函数是正比例函数
1、正比例函数y=kx的图象是经过(0,0)(1,k)的一条直线,
我们把正比例函数y=kx的图象叫做直线y=kx;
2、正比例函数y=kx的图象的画法;
3、正比例函数的性质:
1)图象都经过原点;
2)当k>0时,直线y=kx经过第一、三象限,从左向右上升,
即
y随x的增大而增大;
当k<0时,直线y=kx经过第二、四象限,从左向右下降,
即y随x的增大而减少。
3)
当
|k|
越大时,图像越靠近y轴;
当
|k|
相等时,图像关于坐标轴对称.
本节总结
19.2
一次函数
19.2.1
正比例函数
(第2课时)
1.正比例函数的定义
一般地,形如
y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
2.画函数图象的步骤
列表、描点、连线
-4
-2
0
2
4
y=2x
例1
画正比例函数
y
=2x
的图象
解:
1.
列表
2.
描点
3.
连线
…
…
x
…
-2
-1
0
1
2
…
y
y=2x
比较上面两个函数的图象的相同点与不同点,考虑
两个函数的变化规律.
一般地,正比例函数y=kx(k是常数,k≠0)的图象
直线y=kx经过第一、三象限,
直线y=kx经过第二、四象限,
我们称它为直线y=kx.
正比例函数图象的特征及性质:
是一条经过原点的直线,
当k
>0时,
当k
<0时,
从左向右上升,
即随着x的增大y也增大;
从左向右下降,
即随着x的增大y反而减小.
x
y
0
1
1
当
|k|
越大时,图像越靠近y轴
当
|k|
相等时,图像关于坐标轴对称
补充性质:
如图,三个正比例函数的图象分别对应的解析式是
①y=ax②
y=bx
③
y=cx,则a、b、c的大小关系是(
)
A.a>b>c
B.c>b>a
C.b>a>c
D.b>c>a
x
y
①
②
③
C
1
k
1
k
y=
kx
(k>0)
正比例函数y=
kx
(k≠0)
的图象是经过原点(0,0)和点(1,k)的一条直线。
解:选取两点(0,0)
,
(1,3)
1.画函数
y
=
3x
的图象
y=3x
过这两点画直线,
就是函数y=
3x
的图象
过这两点画直线,
B
二、四
0
-3
减小
1.
正比例函数y=(m-1)x的图象经过一、三象限,
A.
m=1
B.
m>1
C.
m<1
D.
m≥1
3.
函数y=-3x的图象在第
象限内,经过点
2.
正比例函数y=(3-k)
x,如果随着x的增大y反而减
小,则k的取值范围是
______.
k>3
4.
函数y=
x的图象在第
象限内,经过点
(0,
)与点(1,
),y随x的增大而
.
(0,
)与点(1,
),y随x的增大而
.
三、一
0
增大
则m的取值范围是(
)
5.
如果正比例函数y=(8-2a)x的图像经过二、四象限,求a的取值范围。
解:
∴比例系数k=8-2a<0
∴a>4
∵该函数图像经过二、四象限
问:如果正比例函数y=(8-2a)x,y的值随x的值增大而减少,求a的取值范围。
a>4
6.已知正比例函数y=(m+1)xm2
,它的图象经过第几象限?
解:
比例系数k=m+1=2>0
∵该函数是正比例函数
1、正比例函数y=kx的图象是经过(0,0)(1,k)的一条直线,
我们把正比例函数y=kx的图象叫做直线y=kx;
2、正比例函数y=kx的图象的画法;
3、正比例函数的性质:
1)图象都经过原点;
2)当k>0时,直线y=kx经过第一、三象限,从左向右上升,
即
y随x的增大而增大;
当k<0时,直线y=kx经过第二、四象限,从左向右下降,
即y随x的增大而减少。
3)
当
|k|
越大时,图像越靠近y轴;
当
|k|
相等时,图像关于坐标轴对称.
本节总结
