(鄂尔多斯专版)中考数学复习:选择填空常考题型课件-65张
文档属性
| 名称 | (鄂尔多斯专版)中考数学复习:选择填空常考题型课件-65张 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 11:51:08 | ||
图片预览









文档简介
(共65张PPT)
选择填空常考题型突破
规律探索型问题是近几年鄂尔多斯中考命题的热点题型之一,这类题目主要考查学生的数学观察、联想、归纳的能力,大体分为数列规律探究与图形规律探究两种类型,探寻规律要认真观察、仔细思考,善用联想,抓住问题中的变化与不变的因素来分析解决这类问题.探寻数列规律要寻找对应内容与序号之间的关联来解决;图形变化类的规律题首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
类型一 规律探索型问题(2019,15/2018,14/2017,13/2016,15/2014,
16/2013,15)
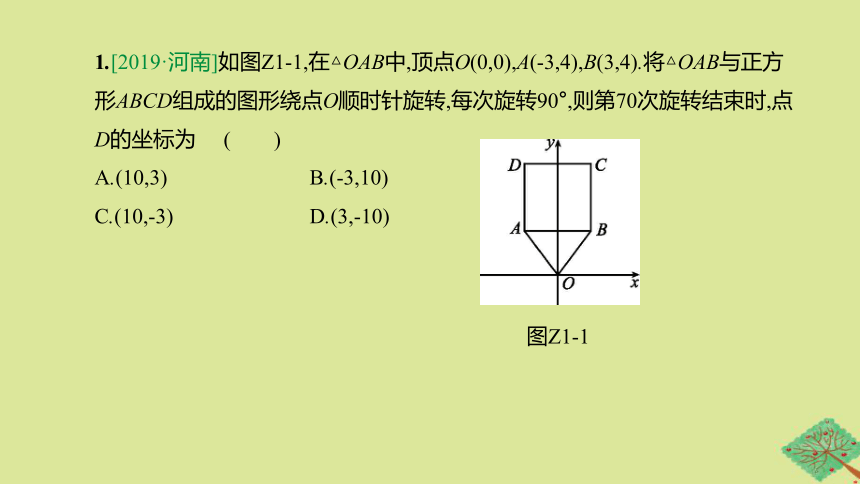
1.[2019·河南]如图Z1-1,在△OAB中,顶点O(0,0),A(-3,4),B(3,4).将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为
( )
A.(10,3)
B.(-3,10)
C.(10,-3)
D.(3,-10)
图Z1-1
[答案]
D
[解析]
延长DA交x轴于点M,
∵A(-3,4),B(3,4),
∴AB=6,AB∥x轴,
∵四边形ABCD为正方形,
∴AD=AB=6,∠DAB=90°,
∴∠DMO=∠DAB=90°,
连接OD,Rt△DMO中,MO=3,DM=10,则D点的坐标为(-3,10),
将△OAB和正方形ABCD组成的图形绕点O每次顺时针旋转90°,
Rt△DMO也同步绕点O每次顺时针旋转90°.
当图形第一次绕点O顺时针旋转90°后,D点的坐标为(10,3),
当图形第二次绕点O顺时针旋转90°后,D点的坐标为(3,-10),
当图形第三次绕点O顺时针旋转90°后,D点的坐标为(-10,-3),
当图形第四次绕点O顺时针旋转90°后,D点的坐标为(-3,10),
当图形第五次绕点O顺时针旋转90°后,D点的坐标为(10,3),
……
每四次为一个循环.
∵70÷4=17……2,
∴旋转70次后,D点的坐标为(3,-10),故选D.
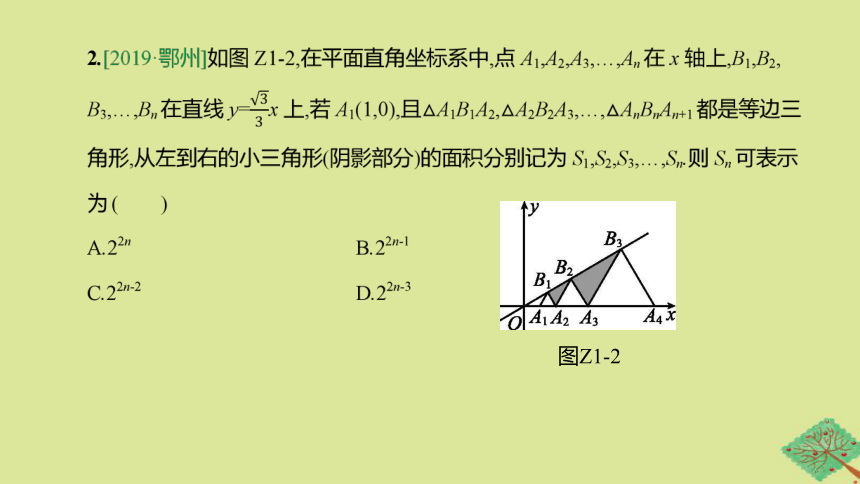
图Z1-2
[答案]
D
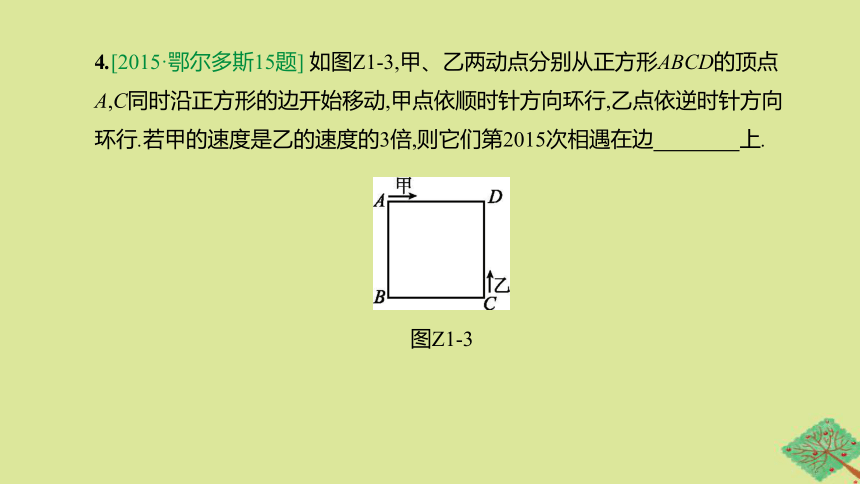
4.[2015·鄂尔多斯15题]
如图Z1-3,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在边 上.?
图Z1-3
[答案]
AB
6.[2018·遵义]
每一层三角形的个数与层数之间的关系如图Z1-4,则第2018层三角形的个数为 .?
图Z1-4
[答案]
4035
[解析]
由题图可知,第1层三角形的个数为1,第2层三角形的个数为3,第3层三角形的个数为5,第4层三角形的个数为7,第5层三角形的个数为9,……,
∴第n层三角形的个数为2n-1,
∴当n=2018时,三角形的个数为2×2018-1=4035.
7.[2017·衢州]
如图Z1-5,正三角形ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,将△ABO沿x轴正方向作无滑动地翻滚,经一次翻滚得△A1B1O,则翻滚3次后点B的对应点的坐标是 ,翻滚2017次后AB中点M经过的路径长为 .?
图Z1-5
8.[2019·鄂尔多斯15题]如图Z1-6,有一条折线A1B1A2B2A3B3A4B4…,它是由过A1(0,0),B1(4,4),A2(8,0)组成的折线依次平移8,16,24,…个单位得到的,直线y=kx+2与此折线有2n(n≥1且n为整数)个交点,则k的值为 .?
图Z1-6
类型二 函数图象问题(2019,10/2018,10/2017,10/2016,10/2015,
10/2013,10)
解决这类问题的关键是“变动为静”,即选取动点运动路径中任意一位置形成静态图形,再由静态图形的性质得出题设变量间的函数关系.
图Z1-7
1.如图Z1-7,在平行四边形ABCD中,AC=4,BD=6,P是BD上的任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E,F.设BP=x,EF=y,则能反映y与x之间关系的图象是
( )
图Z1-7
图Z1-8
[答案]
C
图Z1-9
图Z1-10
[答案]
A
图Z1-11
图Z1-12
[答案]
A
①
②
③
图Z1-13
图Z1-14
A
5.[2019·鄂尔多斯10题]在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行,快车到达B地后,停留3秒卸货,然后原路返回A地,慢车到达A地即停运休息,图Z1-15表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a,b的值分别为
( )
A.39,26
B.39,26.4
C.38,26
D.38,26.4
图Z1-15
[答案]
B
6.[2018·枣庄]
如图Z1-16①,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图②是当点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .?
图Z1-16
[答案]
12
类型三 新定义问题(2019,14/2016,6/2015,14/2014,7/2013,17)
解决此类题目的关键是要理解新定义运算的意义,然后通过试验、探究、猜想,在新定义下解决新问题.
[答案]
B
图Z1-17
[答案]
A
[答案]
C
[答案]
A
图Z1-18
C
6.高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数.
例如,[2.3]=2,[-1.5]=-2.
则有下列结论:
①[-2.1]+[1]=-2;
②[x]+[-x]=0;
③若[x+1]=3,则x的取值范围是2≤x<3;
④当-1≤x<1时,[x+1]+[-x+1]的值为0,1,2.
其中正确的结论是 .(写出所有正确结论的序号)?
[答案]
①③
[解析]
①[-2.1]+[1]=-3+1=-2,正确;
②[x]+[-x]=0,错误,
如[2.5]=2,[-2.5]=-3,2+(-3)≠0;③若[x+1]=3,
则x的取值范围是2≤x<3,正确;
④当-1≤x<1时,0≤x+1<2,0<-x+1≤2,
所以[x+1]的值为0或1,[-x+1]的值为0或1或2,
当[x+1]=0时,[-x+1]=1或2;当[x+1]=1时,[-x+1]=0或1,
所以[x+1]+[-x+1]的值为1或2.
故错误.
[答案]
①②③④
类型四 动点距离最值问题(2017,16/2014,10)
解决两条线段的和最小问题时最基本的依据就是“两点之间,线段最短”,最常见的基本图形就是“将军饮马问题”,在具体问题中要注意其变式.
图Z1-19
[答案]
D
[解析]
连接BD.由题意可得,
当P与D重合时,点F在AD上,点E在BD上,
此时PE+PF最小,
∵菱形ABCD中,∠A=60°,
∴AB=AD,则△ABD是等边三角形,
∴BD=AB=AD=5,
∵☉A,☉B的半径分别为3和2,
∴PE=DE=3,PF=DF=2,
∴PE+PF的最小值是5.故选D.
图Z1-20
[答案]
D
3.[2018·天津]
如图Z1-21,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是
( )
A.AB
B.DE
C.BD
D.AF
图Z1-21
[答案]
D
[解析]如图,取CD的中点E',连接AE',PE'.
由正方形的轴对称的性质可知EP=E'P,AF=AE',
∴AP+EP=AP+E'P,
∴AP+EP的最小值是AE',即AP+EP的最小值是AF.故选D.
图Z1-22
[答案]
A
图Z1-23
[答案]
B
图Z1-24
[答案]
A
7.如图Z1-25,矩形ABCD中,AB=2,AD=3,点E,F分别为AD,DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 .?
图Z1-25
[答案]
4
[解析]∵EF=2,点G为EF的中点,
∴DG=1,G是以D为圆心,以1为半径的圆弧上的点.
作A关于BC的对称点A',连接A'D,交BC于P,交以D为圆心,
以1为半径的圆于G,此时PA+PG的值最小,最小值为A'G的长.
∵AB=2,AD=3,∴AA'=4,
∴A'D=5,∴A'G=A'D-DG=5-1=4,
∴PA+PG的最小值为4.
图Z1-26
[答案]
1
选择填空常考题型突破
规律探索型问题是近几年鄂尔多斯中考命题的热点题型之一,这类题目主要考查学生的数学观察、联想、归纳的能力,大体分为数列规律探究与图形规律探究两种类型,探寻规律要认真观察、仔细思考,善用联想,抓住问题中的变化与不变的因素来分析解决这类问题.探寻数列规律要寻找对应内容与序号之间的关联来解决;图形变化类的规律题首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
类型一 规律探索型问题(2019,15/2018,14/2017,13/2016,15/2014,
16/2013,15)
1.[2019·河南]如图Z1-1,在△OAB中,顶点O(0,0),A(-3,4),B(3,4).将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为
( )
A.(10,3)
B.(-3,10)
C.(10,-3)
D.(3,-10)
图Z1-1
[答案]
D
[解析]
延长DA交x轴于点M,
∵A(-3,4),B(3,4),
∴AB=6,AB∥x轴,
∵四边形ABCD为正方形,
∴AD=AB=6,∠DAB=90°,
∴∠DMO=∠DAB=90°,
连接OD,Rt△DMO中,MO=3,DM=10,则D点的坐标为(-3,10),
将△OAB和正方形ABCD组成的图形绕点O每次顺时针旋转90°,
Rt△DMO也同步绕点O每次顺时针旋转90°.
当图形第一次绕点O顺时针旋转90°后,D点的坐标为(10,3),
当图形第二次绕点O顺时针旋转90°后,D点的坐标为(3,-10),
当图形第三次绕点O顺时针旋转90°后,D点的坐标为(-10,-3),
当图形第四次绕点O顺时针旋转90°后,D点的坐标为(-3,10),
当图形第五次绕点O顺时针旋转90°后,D点的坐标为(10,3),
……
每四次为一个循环.
∵70÷4=17……2,
∴旋转70次后,D点的坐标为(3,-10),故选D.
图Z1-2
[答案]
D
4.[2015·鄂尔多斯15题]
如图Z1-3,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在边 上.?
图Z1-3
[答案]
AB
6.[2018·遵义]
每一层三角形的个数与层数之间的关系如图Z1-4,则第2018层三角形的个数为 .?
图Z1-4
[答案]
4035
[解析]
由题图可知,第1层三角形的个数为1,第2层三角形的个数为3,第3层三角形的个数为5,第4层三角形的个数为7,第5层三角形的个数为9,……,
∴第n层三角形的个数为2n-1,
∴当n=2018时,三角形的个数为2×2018-1=4035.
7.[2017·衢州]
如图Z1-5,正三角形ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,将△ABO沿x轴正方向作无滑动地翻滚,经一次翻滚得△A1B1O,则翻滚3次后点B的对应点的坐标是 ,翻滚2017次后AB中点M经过的路径长为 .?
图Z1-5
8.[2019·鄂尔多斯15题]如图Z1-6,有一条折线A1B1A2B2A3B3A4B4…,它是由过A1(0,0),B1(4,4),A2(8,0)组成的折线依次平移8,16,24,…个单位得到的,直线y=kx+2与此折线有2n(n≥1且n为整数)个交点,则k的值为 .?
图Z1-6
类型二 函数图象问题(2019,10/2018,10/2017,10/2016,10/2015,
10/2013,10)
解决这类问题的关键是“变动为静”,即选取动点运动路径中任意一位置形成静态图形,再由静态图形的性质得出题设变量间的函数关系.
图Z1-7
1.如图Z1-7,在平行四边形ABCD中,AC=4,BD=6,P是BD上的任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E,F.设BP=x,EF=y,则能反映y与x之间关系的图象是
( )
图Z1-7
图Z1-8
[答案]
C
图Z1-9
图Z1-10
[答案]
A
图Z1-11
图Z1-12
[答案]
A
①
②
③
图Z1-13
图Z1-14
A
5.[2019·鄂尔多斯10题]在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行,快车到达B地后,停留3秒卸货,然后原路返回A地,慢车到达A地即停运休息,图Z1-15表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a,b的值分别为
( )
A.39,26
B.39,26.4
C.38,26
D.38,26.4
图Z1-15
[答案]
B
6.[2018·枣庄]
如图Z1-16①,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图②是当点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .?
图Z1-16
[答案]
12
类型三 新定义问题(2019,14/2016,6/2015,14/2014,7/2013,17)
解决此类题目的关键是要理解新定义运算的意义,然后通过试验、探究、猜想,在新定义下解决新问题.
[答案]
B
图Z1-17
[答案]
A
[答案]
C
[答案]
A
图Z1-18
C
6.高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数.
例如,[2.3]=2,[-1.5]=-2.
则有下列结论:
①[-2.1]+[1]=-2;
②[x]+[-x]=0;
③若[x+1]=3,则x的取值范围是2≤x<3;
④当-1≤x<1时,[x+1]+[-x+1]的值为0,1,2.
其中正确的结论是 .(写出所有正确结论的序号)?
[答案]
①③
[解析]
①[-2.1]+[1]=-3+1=-2,正确;
②[x]+[-x]=0,错误,
如[2.5]=2,[-2.5]=-3,2+(-3)≠0;③若[x+1]=3,
则x的取值范围是2≤x<3,正确;
④当-1≤x<1时,0≤x+1<2,0<-x+1≤2,
所以[x+1]的值为0或1,[-x+1]的值为0或1或2,
当[x+1]=0时,[-x+1]=1或2;当[x+1]=1时,[-x+1]=0或1,
所以[x+1]+[-x+1]的值为1或2.
故错误.
[答案]
①②③④
类型四 动点距离最值问题(2017,16/2014,10)
解决两条线段的和最小问题时最基本的依据就是“两点之间,线段最短”,最常见的基本图形就是“将军饮马问题”,在具体问题中要注意其变式.
图Z1-19
[答案]
D
[解析]
连接BD.由题意可得,
当P与D重合时,点F在AD上,点E在BD上,
此时PE+PF最小,
∵菱形ABCD中,∠A=60°,
∴AB=AD,则△ABD是等边三角形,
∴BD=AB=AD=5,
∵☉A,☉B的半径分别为3和2,
∴PE=DE=3,PF=DF=2,
∴PE+PF的最小值是5.故选D.
图Z1-20
[答案]
D
3.[2018·天津]
如图Z1-21,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是
( )
A.AB
B.DE
C.BD
D.AF
图Z1-21
[答案]
D
[解析]如图,取CD的中点E',连接AE',PE'.
由正方形的轴对称的性质可知EP=E'P,AF=AE',
∴AP+EP=AP+E'P,
∴AP+EP的最小值是AE',即AP+EP的最小值是AF.故选D.
图Z1-22
[答案]
A
图Z1-23
[答案]
B
图Z1-24
[答案]
A
7.如图Z1-25,矩形ABCD中,AB=2,AD=3,点E,F分别为AD,DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 .?
图Z1-25
[答案]
4
[解析]∵EF=2,点G为EF的中点,
∴DG=1,G是以D为圆心,以1为半径的圆弧上的点.
作A关于BC的对称点A',连接A'D,交BC于P,交以D为圆心,
以1为半径的圆于G,此时PA+PG的值最小,最小值为A'G的长.
∵AB=2,AD=3,∴AA'=4,
∴A'D=5,∴A'G=A'D-DG=5-1=4,
∴PA+PG的最小值为4.
图Z1-26
[答案]
1
同课章节目录
