(鄂尔多斯专版)中考数学复习——二次函数的综合题课件(共53张PPT)
文档属性
| 名称 | (鄂尔多斯专版)中考数学复习——二次函数的综合题课件(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1010.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 13:43:51 | ||
图片预览








文档简介
(共53张PPT)
二次函数的综合题
类型一 特殊三角形存在性问题(2019,24)
知识储备
1.等腰三角形存在性问题
(1)等腰三角形要分类讨论.
如图Z7-1,当一个三角形为等腰三角形时,存在三种情况:AB=AC;AB=BC;
BC=AC,所以要进行分类讨论.
图Z7-1
图Z7-2
(3)等腰三角形存在性问题.
代数法:若△ABC的边长平方AB2,BC2,AC2方便用勾股定理求解,则由AB2=AC2,BC2=BA2,CA2=CB2分别建立方程,依次求解.
几何法:两圆一线法:如图Z7-3,已知线段AB,在平面内找一点C,使得△ABC为等腰三角形,满足条件的点C如图Z7-3所示(在以点A,B为圆心,AB的长为半径的圆和线段AB的垂直平分线上,除了与点A,B在同一直线上的点外所有的点).
其他方法:可用等腰三角形的性质(作垂线,
三线合一),将证明两腰相等转化为证明中点,或
用相似三角形的性质,或用哪个定角的三角函
数比来建立方程.
图Z7-3
2.直角三角形存在性问题
若△ABC是以AB为直角边的直角三角形,则点C在过点A且垂直于AB的直线或过点B且垂直于AB的直线上.
若△ABC是以BC为斜边的直角三角形,D为斜边BC的中点,则DA=DB=DC,∠BAC=90°.
若以点A,B,C为顶点的三角形是直角三角形,则分三种情况.
几何法:把∠A=90°或∠B=90°或∠C=90°转化为相似三角形对应边成比例建立方程求解;
代数法:用勾股定理表示AB2,BC2,AC2,由AB2+BC2=AC2或AB2+AC2=BC2或BC2+AC2=AB2建立方程依次求解.
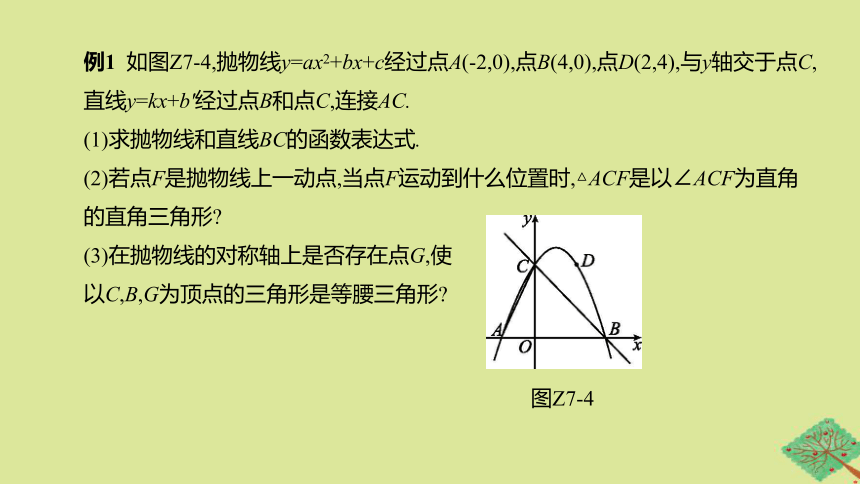
例1
如图Z7-4,抛物线y=ax2+bx+c经过点A(-2,0),点B(4,0),点D(2,4),与y轴交于点C,直线y=kx+b'经过点B和点C,连接AC.
(1)求抛物线和直线BC的函数表达式.
(2)若点F是抛物线上一动点,当点F运动到什么位置时,△ACF是以∠ACF为直角的直角三角形?
(3)在抛物线的对称轴上是否存在点G,使
以C,B,G为顶点的三角形是等腰三角形?
图Z7-4
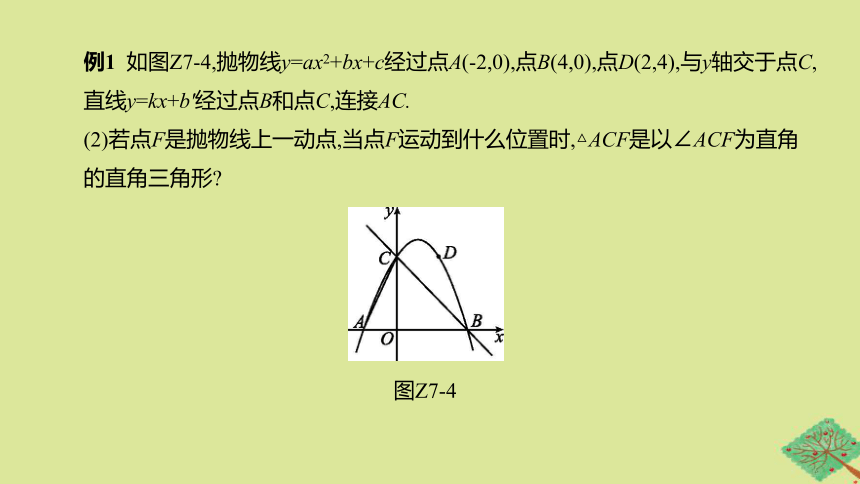
例1
如图Z7-4,抛物线y=ax2+bx+c经过点A(-2,0),点B(4,0),点D(2,4),与y轴交于点C,直线y=kx+b'经过点B和点C,连接AC.
(2)若点F是抛物线上一动点,当点F运动到什么位置时,△ACF是以∠ACF为直角的直角三角形?
图Z7-4
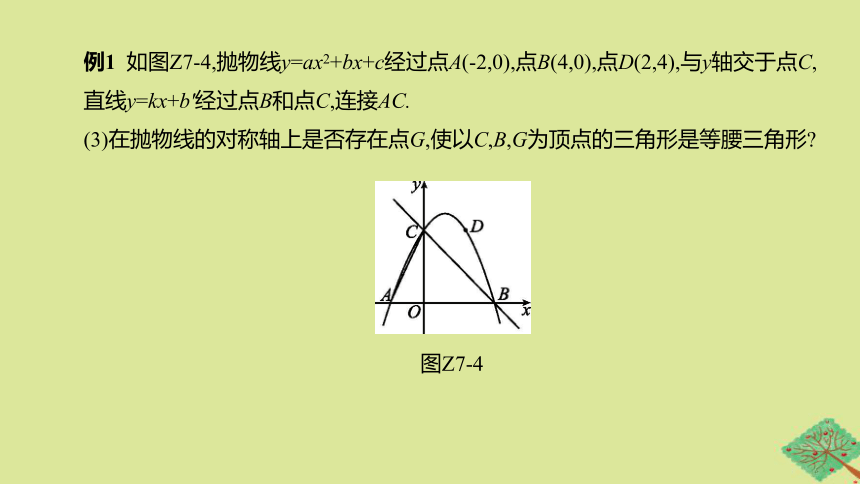
例1
如图Z7-4,抛物线y=ax2+bx+c经过点A(-2,0),点B(4,0),点D(2,4),与y轴交于点C,直线y=kx+b'经过点B和点C,连接AC.
(3)在抛物线的对称轴上是否存在点G,使以C,B,G为顶点的三角形是等腰三角形?
图Z7-4
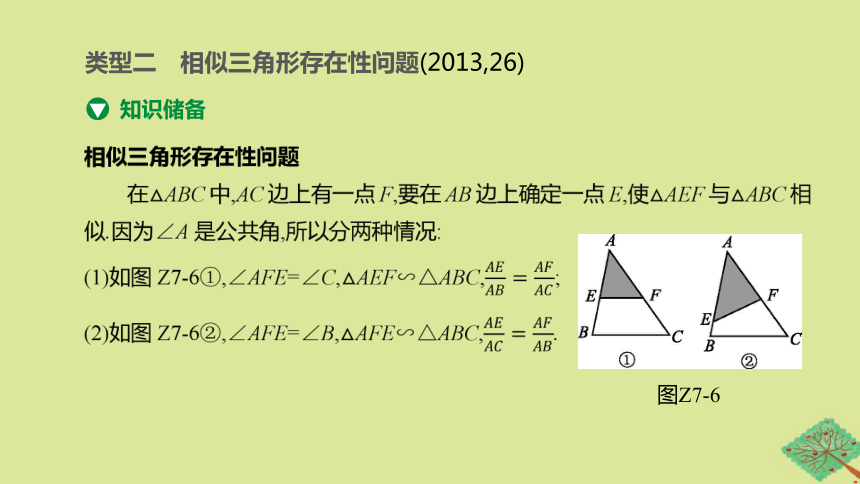
类型二 相似三角形存在性问题(2013,26)
知识储备
图Z7-6
注意事项:
(1)求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形.
(2)根据已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小.
(3)若两个三角形的各边均未给出,则应先设
所求点的坐标,进而用函数解析式来表示各
边的长度,之后利用相似来列方程求解.
图Z7-6
图Z7-7
(4)设抛物线的对称轴与x轴相交于点E,点P是位于直线BC上方抛物线上的一动点,连接PE,交CB于F.当△BEF与△ACB相似时,求点P的坐标.
(5)若点Q是线段BC上一动点,是否存在点Q,使△AOC与△OCQ相似?若存在,求出点Q的坐标;若不存在,请说明理由.
图Z7-7
图Z7-7
图Z7-7
图Z7-7
图Z7-7
类型三 二次函数与四边形的结合(2018,23/2017,23/2015,24/2013,
26)
知识储备
1.平行四边形存在性问题
题型
3个定点+1个动点
2个定点+2个动点
例图
(续表)
题型
3个定点+1个动点
2个定点+2个动点
例图
A,M,N为定点,D为动点
A,C为两个定点,另两个动点中一点在x轴上,另一点在抛物线上
(续表)
知识原理
平行四边形的对边平行且相等,对角线互相平分(中心对称性)
解
题
策
略
方法
具体思路
适用情况
(1)直接
计算法
根据已知两点的连线为边,或者为对角线分两大类,分别计算
已知两点的连线在坐标轴上或平行于坐标轴
(2)构
造全
等法
过平行四边形的某两个顶点作坐标轴的垂线,利用平行四边形一组对边所在的两个三角形全等,把平行且相等的对边转化为水平或者垂直方向的两条对应边相等
已知两点的连线不与坐标轴平行;
容易画出草图
(续表)
解
题
策
略
方法
具体思路
适用情况
(3)中
心对
称法
已知两点的连线为对角线时,它的中点也是另外待定的两点连线的中点,设待定两点的坐标,用中点坐标公式表示其中点坐标,由中点重合,建立方程(组)即可
已知两点的连线不与坐标轴平行;
不方便画出草图
(4)平
移坐
标法
利用平移的意义,根据已知两点间横、纵坐标的距离关系,得待定两点也有同样的数量关系
已知两点的连线不与坐标轴平行;
仅适用于不要去书写过程的题目
2.矩形存在性问题
由于矩形是含90°角的平行四边形,因此,解决矩形存在性问题,需要综合平行四边形和直角三角形存在性问题的方法.
3.菱形存在性问题
由于菱形是一组邻边相等的平行四边形,因此,解决菱形存在性问题,需要综合平行四边形和等腰三角形存在性问题的方法.
4.正方形存在性问题
由于正方形既是矩形也是菱形,因此,解决正方形存在性问题,需要灵活选用所有存在性问题的方法.
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(1)求此抛物线的解析式,顶点M的坐标,对称轴l;
图Z7-10
(2)抛物线沿直线AB平移,使得点A落在点B处,此时点C的对应点为C',求C'的坐标,
试判断四边形ABC'C的形状,并说明理由;
图Z7-10
(3)设点C'是平面内一点,是否存在以点A,B,C,C'为顶点的四边形是平行四边形.若存在,求出点C'的坐标,若不存在,请说明理由;
图Z7-10
(4)设点G是抛物线对称轴上一点,点K是平面内一点,是否存在点G,使得以A,C,G,
K为顶点的四边形是矩形,若存在,求出点G的坐标,若不存在,请说明理由;
图Z7-10
(5)设点G是抛物线对称轴上一点,过点G作平行于AB的一条直线l',点K在l'上,若以A,O,G,K为顶点的四边形是菱形,写出所有满足条件的点G,点K坐标;
图Z7-10
(6)设点P是抛物线对称轴上一点,点Q是平面内一点,是否存在以A,P,Q,E为顶点的四边形为正方形,若存在,求出点P,Q的坐标,若不存在,请说明理由.
图Z7-10
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(2)抛物线沿直线AB平移,使得点A落在点B处,此时点C的对应点为C',求C'的坐标,
试判断四边形ABC'C的形状,并说明理由;
图Z7-10
解:
(2)如图①,∵A(-5,0),B(-1,0),C(0,5),
∴C'(4,5),
∴四边形ABC'C是平行四边形.
理由如下:根据平移性质得:
AB=CC'=4,AB∥CC',
∴四边形ABC'C是平行四边形.
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(3)设点C'是平面内一点,是否存在以点A,B,C,C'为顶点的四边形是平行四边形.若存在,求出点C'的坐标,若不存在,请说明理由;
图Z7-10
解:
(3)存在,理由如下:
(i)当线段AB为平行四边形的边时,
当点C'在点C右侧时,如图①,将线段AB沿AC平移,使点A与点C重合,此时点C'坐标为(4,5);
当点C'在点C左侧时,如图②,将线段BC沿BA平移,使点B与点A重合,此时点C'的坐标为(-4,5);
(ii)当线段AB为平行四边形对角线时,如图③,
将线段AC沿CB平移,使点C与点B重合,此时
点C'的坐标为(-6,-5).
综上所述,满足条件的点C'的坐标为(4,5),(-6,-5),(-4,5).
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(4)设点G是抛物线对称轴上一点,点K是平面内一点,是否存在点G,使得以A,C,G,
K为顶点的四边形是矩形,若存在,求出点G的坐标,若不存在,请说明理由;
图Z7-10
解:
(4)存在.理由如下:
以A,C,G,K为顶点的四边形是矩形,则△ACG一定是直角三角形,如图④,
设点G的坐标为(-3,g),
作GH⊥y轴于点H(以图④中G1为例).
∵AC2=52+52=50,
AG2=(5-3)2+g2=4+g2,
CG2=32+(5-g)2=g2-10g+34.
(i)若∠ACG=90°,则AC2+CG2=AG2,
即50+g2-10g+34=4+g2,解得g=8,
此时点G的坐标为(-3,8);
(ii)若∠CAG=90°,则AC2+AG2=CG2.
即50+4+g2=g2-10g+34,解得g=-2,
此时点G的坐标为(-3,-2);
(iii)若∠CGA=90°,则CG2+AG2=AC2,
即g2-10g+34+4+g2=50,解得g1=6,g2=-1,
此时点G的坐标为(-3,6)或(-3,-1).
综上所述,满足条件的点G共有4个,分别为(-3,8),(-3,6),(-3,-1),(-3,-2);
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(5)设点G是抛物线对称轴上一点,过点G作平行于AB的一条直线l',点K在l'上,若以A,O,G,K为顶点的四边形是菱形,写出所有满足条件的点G,点K坐标;
图Z7-10
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(6)设点P是抛物线对称轴上一点,点Q是平面内一点,是否存在以A,P,Q,E为顶点的四边形为正方形,若存在,求出点P,Q的坐标,若不存在,请说明理由.
图Z7-10
解:
(6)存在,理由如下:
∵点P在抛物线对称轴上,∴设点P(-3,t).
如图⑥,当AE是正方形的边时,点E与点P1关于AB对称,点Q1与点B重合,
∴点P1的坐标为(-3,-2),点Q1的坐标为(-1,0);
当AE是正方形的对角线时,点P2与点D重合,
∴点P2的坐标为(-3,0),点Q2的坐标为(-5,2).
【方法点析】平行四边形存在性问题,如果已经确定了对边平行关系,那么只需要根据对边相等列出方程即可求解;如果是由两个定点、两个动点构成的平行四边形,往往需要确定哪条边为对角线来作为分类的标准,分成三类,可以设两个未知数,然后根据对角线互相平分,即两条对角线中点重合来列方程组求解即可.
矩形存在性问题,可以转化为直角三角形存在性问题;菱形存在性问题,可以转化为等腰三角形存在性问题;正方形存在性问题,可以转化为等腰直角三角形存在性问题.
类型四 二次函数与圆的结合(2019,24/2014,24)
例4[2019·鄂尔多斯改编]如图Z7-14,抛物线y=ax2+bx-2(a≠0)与x轴交于A(-3,0),
B(1,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)求△ABC外接圆圆心N的坐标;
(3)变式1:以点C为圆心,1为半径作☉C,过点B作☉C的切线,求切点M的坐标;
(4)变式2:直线y=k与抛物线
交于E,F两点,以EF为直径
的☉M与x轴相切,求k的值.
图Z7-14
例4[2019·鄂尔多斯改编]如图Z7-14,抛物线y=ax2+bx-2(a≠0)与x轴交于A(-3,0),
B(1,0)两点,与y轴交于点C.
(2)求△ABC外接圆圆心N的坐标;
图Z7-14
例4[2019·鄂尔多斯改编]如图Z7-14,抛物线y=ax2+bx-2(a≠0)与x轴交于A(-3,0),
B(1,0)两点,与y轴交于点C.
(3)变式1:以点C为圆心,1为半径作☉C,过点B作☉C的切线,求切点M的坐标;
图Z7-14
例4[2019·鄂尔多斯改编]如图Z7-14,抛物线y=ax2+bx-2(a≠0)与x轴交于A(-3,0),
B(1,0)两点,与y轴交于点C.
(4)变式2:直线y=k与抛物线交于E,F两点,以EF为直径的☉M与x轴相切,求k的值.
图Z7-14
二次函数的综合题
类型一 特殊三角形存在性问题(2019,24)
知识储备
1.等腰三角形存在性问题
(1)等腰三角形要分类讨论.
如图Z7-1,当一个三角形为等腰三角形时,存在三种情况:AB=AC;AB=BC;
BC=AC,所以要进行分类讨论.
图Z7-1
图Z7-2
(3)等腰三角形存在性问题.
代数法:若△ABC的边长平方AB2,BC2,AC2方便用勾股定理求解,则由AB2=AC2,BC2=BA2,CA2=CB2分别建立方程,依次求解.
几何法:两圆一线法:如图Z7-3,已知线段AB,在平面内找一点C,使得△ABC为等腰三角形,满足条件的点C如图Z7-3所示(在以点A,B为圆心,AB的长为半径的圆和线段AB的垂直平分线上,除了与点A,B在同一直线上的点外所有的点).
其他方法:可用等腰三角形的性质(作垂线,
三线合一),将证明两腰相等转化为证明中点,或
用相似三角形的性质,或用哪个定角的三角函
数比来建立方程.
图Z7-3
2.直角三角形存在性问题
若△ABC是以AB为直角边的直角三角形,则点C在过点A且垂直于AB的直线或过点B且垂直于AB的直线上.
若△ABC是以BC为斜边的直角三角形,D为斜边BC的中点,则DA=DB=DC,∠BAC=90°.
若以点A,B,C为顶点的三角形是直角三角形,则分三种情况.
几何法:把∠A=90°或∠B=90°或∠C=90°转化为相似三角形对应边成比例建立方程求解;
代数法:用勾股定理表示AB2,BC2,AC2,由AB2+BC2=AC2或AB2+AC2=BC2或BC2+AC2=AB2建立方程依次求解.
例1
如图Z7-4,抛物线y=ax2+bx+c经过点A(-2,0),点B(4,0),点D(2,4),与y轴交于点C,直线y=kx+b'经过点B和点C,连接AC.
(1)求抛物线和直线BC的函数表达式.
(2)若点F是抛物线上一动点,当点F运动到什么位置时,△ACF是以∠ACF为直角的直角三角形?
(3)在抛物线的对称轴上是否存在点G,使
以C,B,G为顶点的三角形是等腰三角形?
图Z7-4
例1
如图Z7-4,抛物线y=ax2+bx+c经过点A(-2,0),点B(4,0),点D(2,4),与y轴交于点C,直线y=kx+b'经过点B和点C,连接AC.
(2)若点F是抛物线上一动点,当点F运动到什么位置时,△ACF是以∠ACF为直角的直角三角形?
图Z7-4
例1
如图Z7-4,抛物线y=ax2+bx+c经过点A(-2,0),点B(4,0),点D(2,4),与y轴交于点C,直线y=kx+b'经过点B和点C,连接AC.
(3)在抛物线的对称轴上是否存在点G,使以C,B,G为顶点的三角形是等腰三角形?
图Z7-4
类型二 相似三角形存在性问题(2013,26)
知识储备
图Z7-6
注意事项:
(1)求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形.
(2)根据已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小.
(3)若两个三角形的各边均未给出,则应先设
所求点的坐标,进而用函数解析式来表示各
边的长度,之后利用相似来列方程求解.
图Z7-6
图Z7-7
(4)设抛物线的对称轴与x轴相交于点E,点P是位于直线BC上方抛物线上的一动点,连接PE,交CB于F.当△BEF与△ACB相似时,求点P的坐标.
(5)若点Q是线段BC上一动点,是否存在点Q,使△AOC与△OCQ相似?若存在,求出点Q的坐标;若不存在,请说明理由.
图Z7-7
图Z7-7
图Z7-7
图Z7-7
图Z7-7
类型三 二次函数与四边形的结合(2018,23/2017,23/2015,24/2013,
26)
知识储备
1.平行四边形存在性问题
题型
3个定点+1个动点
2个定点+2个动点
例图
(续表)
题型
3个定点+1个动点
2个定点+2个动点
例图
A,M,N为定点,D为动点
A,C为两个定点,另两个动点中一点在x轴上,另一点在抛物线上
(续表)
知识原理
平行四边形的对边平行且相等,对角线互相平分(中心对称性)
解
题
策
略
方法
具体思路
适用情况
(1)直接
计算法
根据已知两点的连线为边,或者为对角线分两大类,分别计算
已知两点的连线在坐标轴上或平行于坐标轴
(2)构
造全
等法
过平行四边形的某两个顶点作坐标轴的垂线,利用平行四边形一组对边所在的两个三角形全等,把平行且相等的对边转化为水平或者垂直方向的两条对应边相等
已知两点的连线不与坐标轴平行;
容易画出草图
(续表)
解
题
策
略
方法
具体思路
适用情况
(3)中
心对
称法
已知两点的连线为对角线时,它的中点也是另外待定的两点连线的中点,设待定两点的坐标,用中点坐标公式表示其中点坐标,由中点重合,建立方程(组)即可
已知两点的连线不与坐标轴平行;
不方便画出草图
(4)平
移坐
标法
利用平移的意义,根据已知两点间横、纵坐标的距离关系,得待定两点也有同样的数量关系
已知两点的连线不与坐标轴平行;
仅适用于不要去书写过程的题目
2.矩形存在性问题
由于矩形是含90°角的平行四边形,因此,解决矩形存在性问题,需要综合平行四边形和直角三角形存在性问题的方法.
3.菱形存在性问题
由于菱形是一组邻边相等的平行四边形,因此,解决菱形存在性问题,需要综合平行四边形和等腰三角形存在性问题的方法.
4.正方形存在性问题
由于正方形既是矩形也是菱形,因此,解决正方形存在性问题,需要灵活选用所有存在性问题的方法.
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(1)求此抛物线的解析式,顶点M的坐标,对称轴l;
图Z7-10
(2)抛物线沿直线AB平移,使得点A落在点B处,此时点C的对应点为C',求C'的坐标,
试判断四边形ABC'C的形状,并说明理由;
图Z7-10
(3)设点C'是平面内一点,是否存在以点A,B,C,C'为顶点的四边形是平行四边形.若存在,求出点C'的坐标,若不存在,请说明理由;
图Z7-10
(4)设点G是抛物线对称轴上一点,点K是平面内一点,是否存在点G,使得以A,C,G,
K为顶点的四边形是矩形,若存在,求出点G的坐标,若不存在,请说明理由;
图Z7-10
(5)设点G是抛物线对称轴上一点,过点G作平行于AB的一条直线l',点K在l'上,若以A,O,G,K为顶点的四边形是菱形,写出所有满足条件的点G,点K坐标;
图Z7-10
(6)设点P是抛物线对称轴上一点,点Q是平面内一点,是否存在以A,P,Q,E为顶点的四边形为正方形,若存在,求出点P,Q的坐标,若不存在,请说明理由.
图Z7-10
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(2)抛物线沿直线AB平移,使得点A落在点B处,此时点C的对应点为C',求C'的坐标,
试判断四边形ABC'C的形状,并说明理由;
图Z7-10
解:
(2)如图①,∵A(-5,0),B(-1,0),C(0,5),
∴C'(4,5),
∴四边形ABC'C是平行四边形.
理由如下:根据平移性质得:
AB=CC'=4,AB∥CC',
∴四边形ABC'C是平行四边形.
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(3)设点C'是平面内一点,是否存在以点A,B,C,C'为顶点的四边形是平行四边形.若存在,求出点C'的坐标,若不存在,请说明理由;
图Z7-10
解:
(3)存在,理由如下:
(i)当线段AB为平行四边形的边时,
当点C'在点C右侧时,如图①,将线段AB沿AC平移,使点A与点C重合,此时点C'坐标为(4,5);
当点C'在点C左侧时,如图②,将线段BC沿BA平移,使点B与点A重合,此时点C'的坐标为(-4,5);
(ii)当线段AB为平行四边形对角线时,如图③,
将线段AC沿CB平移,使点C与点B重合,此时
点C'的坐标为(-6,-5).
综上所述,满足条件的点C'的坐标为(4,5),(-6,-5),(-4,5).
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(4)设点G是抛物线对称轴上一点,点K是平面内一点,是否存在点G,使得以A,C,G,
K为顶点的四边形是矩形,若存在,求出点G的坐标,若不存在,请说明理由;
图Z7-10
解:
(4)存在.理由如下:
以A,C,G,K为顶点的四边形是矩形,则△ACG一定是直角三角形,如图④,
设点G的坐标为(-3,g),
作GH⊥y轴于点H(以图④中G1为例).
∵AC2=52+52=50,
AG2=(5-3)2+g2=4+g2,
CG2=32+(5-g)2=g2-10g+34.
(i)若∠ACG=90°,则AC2+CG2=AG2,
即50+g2-10g+34=4+g2,解得g=8,
此时点G的坐标为(-3,8);
(ii)若∠CAG=90°,则AC2+AG2=CG2.
即50+4+g2=g2-10g+34,解得g=-2,
此时点G的坐标为(-3,-2);
(iii)若∠CGA=90°,则CG2+AG2=AC2,
即g2-10g+34+4+g2=50,解得g1=6,g2=-1,
此时点G的坐标为(-3,6)或(-3,-1).
综上所述,满足条件的点G共有4个,分别为(-3,8),(-3,6),(-3,-1),(-3,-2);
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(5)设点G是抛物线对称轴上一点,过点G作平行于AB的一条直线l',点K在l'上,若以A,O,G,K为顶点的四边形是菱形,写出所有满足条件的点G,点K坐标;
图Z7-10
例3
如图Z7-10①,抛物线经过点A(-5,0),B(-1,0),C(0,5)三点,顶点为M,连接AC,BC,抛物线的对称轴为l,l与x轴交于点D,与AC交于点E.
(6)设点P是抛物线对称轴上一点,点Q是平面内一点,是否存在以A,P,Q,E为顶点的四边形为正方形,若存在,求出点P,Q的坐标,若不存在,请说明理由.
图Z7-10
解:
(6)存在,理由如下:
∵点P在抛物线对称轴上,∴设点P(-3,t).
如图⑥,当AE是正方形的边时,点E与点P1关于AB对称,点Q1与点B重合,
∴点P1的坐标为(-3,-2),点Q1的坐标为(-1,0);
当AE是正方形的对角线时,点P2与点D重合,
∴点P2的坐标为(-3,0),点Q2的坐标为(-5,2).
【方法点析】平行四边形存在性问题,如果已经确定了对边平行关系,那么只需要根据对边相等列出方程即可求解;如果是由两个定点、两个动点构成的平行四边形,往往需要确定哪条边为对角线来作为分类的标准,分成三类,可以设两个未知数,然后根据对角线互相平分,即两条对角线中点重合来列方程组求解即可.
矩形存在性问题,可以转化为直角三角形存在性问题;菱形存在性问题,可以转化为等腰三角形存在性问题;正方形存在性问题,可以转化为等腰直角三角形存在性问题.
类型四 二次函数与圆的结合(2019,24/2014,24)
例4[2019·鄂尔多斯改编]如图Z7-14,抛物线y=ax2+bx-2(a≠0)与x轴交于A(-3,0),
B(1,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)求△ABC外接圆圆心N的坐标;
(3)变式1:以点C为圆心,1为半径作☉C,过点B作☉C的切线,求切点M的坐标;
(4)变式2:直线y=k与抛物线
交于E,F两点,以EF为直径
的☉M与x轴相切,求k的值.
图Z7-14
例4[2019·鄂尔多斯改编]如图Z7-14,抛物线y=ax2+bx-2(a≠0)与x轴交于A(-3,0),
B(1,0)两点,与y轴交于点C.
(2)求△ABC外接圆圆心N的坐标;
图Z7-14
例4[2019·鄂尔多斯改编]如图Z7-14,抛物线y=ax2+bx-2(a≠0)与x轴交于A(-3,0),
B(1,0)两点,与y轴交于点C.
(3)变式1:以点C为圆心,1为半径作☉C,过点B作☉C的切线,求切点M的坐标;
图Z7-14
例4[2019·鄂尔多斯改编]如图Z7-14,抛物线y=ax2+bx-2(a≠0)与x轴交于A(-3,0),
B(1,0)两点,与y轴交于点C.
(4)变式2:直线y=k与抛物线交于E,F两点,以EF为直径的☉M与x轴相切,求k的值.
图Z7-14
同课章节目录
