人教版九年级数学上册21.2.1 配方法课件(1)(22张PPT)
文档属性
| 名称 | 人教版九年级数学上册21.2.1 配方法课件(1)(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 236.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 10:53:58 | ||
图片预览

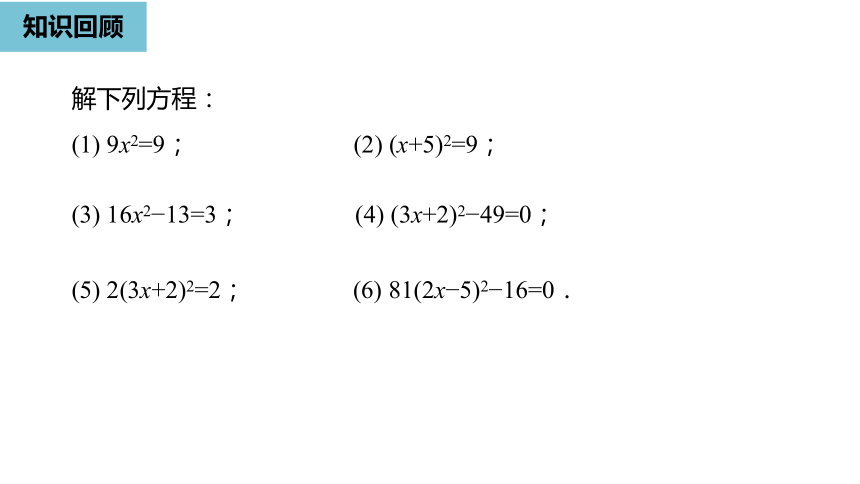
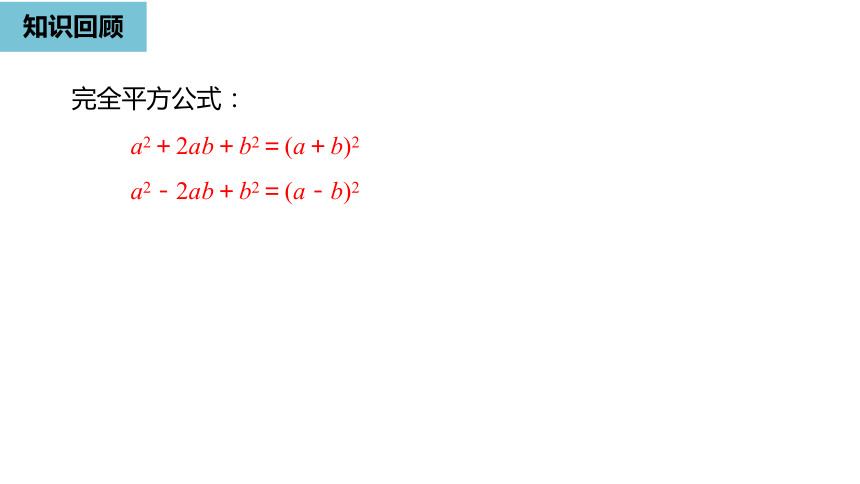





文档简介
(共22张PPT)
21.2.1
配方法
一元二次方程
人教版-数学-九年级上册
知识回顾
解下列方程:
(1)
9x2=9;
(2)
(x+5)2=9;
(3)
16x2?13=3;
(4)
(3x+2)2?49=0;
(5)
2(3x+2)2=2;
(6)
81(2x?5)2?16=0.
知识回顾
完全平方公式:
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
学习目标
1.理解一元二次方程配方的方法.
2.掌握用配方法解一元二次方程.
课堂导入
读诗词解题:
(通过列方程,算出周瑜去世时的年龄)
大江东去浪淘尽,千古风流数人物.
而立之年督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符.
哪位学子算得快,多少年华属周瑜?
解:设个位数字为x,十位数字为x?3.
x2?11x+30=0
x2=10(x?3)+x
知识点1
新知探究
根据完全平方公式:a2±2ab+b2=(a±b)2
完成填空:
(1)
x2–4x+____=(x–____)2
(2)
x2+12x+____=(x+____)2
(3)
y2–8y+____=(y–____)2
思考:你所填写的
b,b2
与一次项的系数有怎样的关系?
二次项系数为
1
的完全平方式:常数项等于一次项系数一半的平方.
4
2
36
6
16
4
知识点1
新知探究
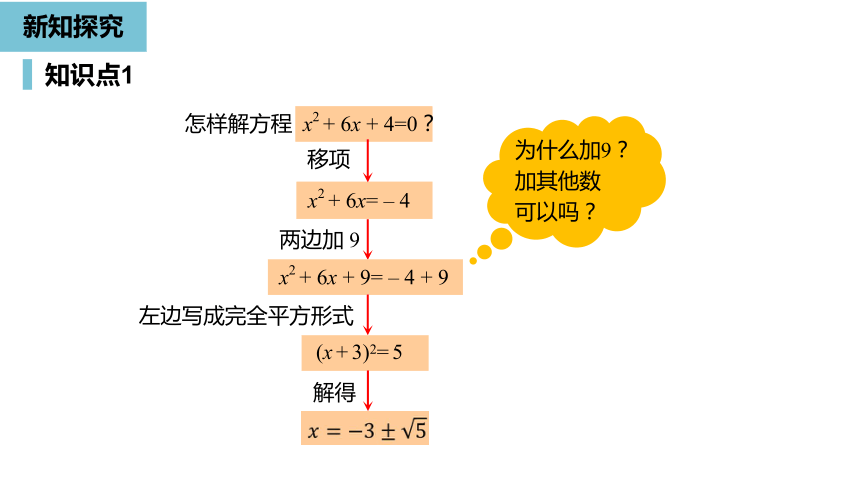
移项
x2
+
6x=
–
4
两边加
9
x2
+
6x
+
9=
–
4
+
9
左边写成完全平方形式
(x
+
3)2=
5
为什么加9?加其他数可以吗?
解得
怎样解方程
x2
+
6x
+
4=0?
知识点1
新知探究
通过配成完全平方形式来解一元二次方程的方法,叫做配方法
.
用配方法解一元二次方程的基本思路:
把方程化为
(x
+
n)2=
p
的形式
将一元二次方程降次
转化为一元一次方程求解
知识点1
新知探究
用配方法解一元二次方程的一般步骤:
一般步骤
方法
一移
移项
将常数项移到等号右边,含未知数的项移到等号左边
二化
二次项系数化为1
左、右两边同时除以二次项系数
三配
配方
左、右两边同时加上一次项系数一半的平方
四开
开平方求根
利用平方根的意义直接开平方
知识点1
新知探究
配方法的依据是完全平方公式的逆用
a2±2ab+b2=(a±b)2
和直接开平方法,其实质是对一元二次方程进行变形,使其转化为能够直接开平方的方程形式,从而把一元二次方程转化成两个一元一次方程来解.
知识点1
新知探究
一般地,如果一个一元二次方程通过配方转化成
(x+n)2=p
的形式,那么就有:
(1)当
p>0
时,方程有两个不等的实数根
x1=-n-,x2=﹣n+
;
(2)当
p=0
时,方程有两个相等的实数根
x1=x2=-n;
(3)当
p<0
时,因为对任意实数
x
,都有
(x+n)2≥0,所以方程无实数根.
跟踪训练
新知探究
大江东去浪淘尽,千古风流数人物.
而立之年督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符.
哪位学子算得快,多少年华属周瑜?
x2?11x+30=0
x=5或x=6
年龄为25或36岁,而立之年是三十岁,
所以周瑜去世时的年龄为36岁.
解:设个位数字为x,十位数字为x?3.
x2=10(x?3)+x
跟踪训练
新知探究
解下列方程:
(1)x2-8x+1=0;
(2)2x2+1=3x;
(3)
3x2-6x+4=0.
解: (1)移项,得
x2-8x=-1.
配方,得
x2-8x+42=-1+42,
(x-4)2=15.
由此可得
跟踪训练
新知探究
(2)
移项,得
2x2-3x=-1.
二次项系数化为1,得
配方,得
由此可得
解下列方程:
(1)x2-8x+1=0;
(2)2x2+1=3x;
(3)
3x2-6x+4=0.
解:
跟踪训练
新知探究
(3)移项,得
3x2-6x=-4,
二次项系数化为1,得
配方,得
因为实数的平方不会是负数,所以x取任何实数时,
(x-1)2
都是非负数,上式都不成立,即原方程无实数根.
x2-2x=
.
x2-2x
+
12
=
+
12.
(x-1)2=
.
解下列方程:
(1)x2-8x+1=0;
(2)2x2+1=3x;
(3)
3x2-6x+4=0.
解:
随堂练习
1
填空:
(1)x2+10x+____=(x+____)2;
(2)x2-12x+____=(x-____)2;
(3)x2+5x+____=(x+____)2;
(4)x2-
x+____=(x-____)2.
25
5
36
6
随堂练习
2
解:(1)移项,得x2-x=,
配方,得x2-x+
=
+
,
(x-
)2=2,
由此可得,x-
=±
,
x1=
+
,x2=
-
.
解下列方程:
(1)x2-x-
=0;
(2)x(x+4)=8x+12.
随堂练习
2
解下列方程:
(1)x2-x-
=0;
(2)x(x+4)=8x+12.
解:
(2)去括号,移项,合并同类项,得x2-4x=12,
配方,得x2-4x+4=12+4,(x-2)2=16,
由此可得x-2=±4,x1=6,x2=-2.
课堂小结
1.
通过配成完全平方的形式来解一元二次方程的方法,
叫做配方法.
2.
用配方法解一元二次方程的一般步骤:
一移
→
二化
→
三配→
四开.
对接中考
1
一元二次方程
配方后可化为(
)
A.
B.
C.
D.
B
对接中考
2
若将一元二次方程
x2-8x-9=0
化成
(x+n)2=d
的形式,则n=
,d=
.
-4
25
x2-8x-9=0,
x2-8x=9,
移项得
配方
x2-8x+
42
=9+
42
,
所以
(x-4)2=25,
即
n=-
4,d=25.
解:
对接中考
3
已知方程
x2-6x+q=0
配方后是
(x-p)2=7
,那么方程
x2+6x+q=0
配方后是(
)
A.(x-p)2=5
B.(x+p)2=5
C.(x-p)2=7
D.(x+p)2=7
D
21.2.1
配方法
一元二次方程
人教版-数学-九年级上册
知识回顾
解下列方程:
(1)
9x2=9;
(2)
(x+5)2=9;
(3)
16x2?13=3;
(4)
(3x+2)2?49=0;
(5)
2(3x+2)2=2;
(6)
81(2x?5)2?16=0.
知识回顾
完全平方公式:
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
学习目标
1.理解一元二次方程配方的方法.
2.掌握用配方法解一元二次方程.
课堂导入
读诗词解题:
(通过列方程,算出周瑜去世时的年龄)
大江东去浪淘尽,千古风流数人物.
而立之年督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符.
哪位学子算得快,多少年华属周瑜?
解:设个位数字为x,十位数字为x?3.
x2?11x+30=0
x2=10(x?3)+x
知识点1
新知探究
根据完全平方公式:a2±2ab+b2=(a±b)2
完成填空:
(1)
x2–4x+____=(x–____)2
(2)
x2+12x+____=(x+____)2
(3)
y2–8y+____=(y–____)2
思考:你所填写的
b,b2
与一次项的系数有怎样的关系?
二次项系数为
1
的完全平方式:常数项等于一次项系数一半的平方.
4
2
36
6
16
4
知识点1
新知探究
移项
x2
+
6x=
–
4
两边加
9
x2
+
6x
+
9=
–
4
+
9
左边写成完全平方形式
(x
+
3)2=
5
为什么加9?加其他数可以吗?
解得
怎样解方程
x2
+
6x
+
4=0?
知识点1
新知探究
通过配成完全平方形式来解一元二次方程的方法,叫做配方法
.
用配方法解一元二次方程的基本思路:
把方程化为
(x
+
n)2=
p
的形式
将一元二次方程降次
转化为一元一次方程求解
知识点1
新知探究
用配方法解一元二次方程的一般步骤:
一般步骤
方法
一移
移项
将常数项移到等号右边,含未知数的项移到等号左边
二化
二次项系数化为1
左、右两边同时除以二次项系数
三配
配方
左、右两边同时加上一次项系数一半的平方
四开
开平方求根
利用平方根的意义直接开平方
知识点1
新知探究
配方法的依据是完全平方公式的逆用
a2±2ab+b2=(a±b)2
和直接开平方法,其实质是对一元二次方程进行变形,使其转化为能够直接开平方的方程形式,从而把一元二次方程转化成两个一元一次方程来解.
知识点1
新知探究
一般地,如果一个一元二次方程通过配方转化成
(x+n)2=p
的形式,那么就有:
(1)当
p>0
时,方程有两个不等的实数根
x1=-n-,x2=﹣n+
;
(2)当
p=0
时,方程有两个相等的实数根
x1=x2=-n;
(3)当
p<0
时,因为对任意实数
x
,都有
(x+n)2≥0,所以方程无实数根.
跟踪训练
新知探究
大江东去浪淘尽,千古风流数人物.
而立之年督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符.
哪位学子算得快,多少年华属周瑜?
x2?11x+30=0
x=5或x=6
年龄为25或36岁,而立之年是三十岁,
所以周瑜去世时的年龄为36岁.
解:设个位数字为x,十位数字为x?3.
x2=10(x?3)+x
跟踪训练
新知探究
解下列方程:
(1)x2-8x+1=0;
(2)2x2+1=3x;
(3)
3x2-6x+4=0.
解: (1)移项,得
x2-8x=-1.
配方,得
x2-8x+42=-1+42,
(x-4)2=15.
由此可得
跟踪训练
新知探究
(2)
移项,得
2x2-3x=-1.
二次项系数化为1,得
配方,得
由此可得
解下列方程:
(1)x2-8x+1=0;
(2)2x2+1=3x;
(3)
3x2-6x+4=0.
解:
跟踪训练
新知探究
(3)移项,得
3x2-6x=-4,
二次项系数化为1,得
配方,得
因为实数的平方不会是负数,所以x取任何实数时,
(x-1)2
都是非负数,上式都不成立,即原方程无实数根.
x2-2x=
.
x2-2x
+
12
=
+
12.
(x-1)2=
.
解下列方程:
(1)x2-8x+1=0;
(2)2x2+1=3x;
(3)
3x2-6x+4=0.
解:
随堂练习
1
填空:
(1)x2+10x+____=(x+____)2;
(2)x2-12x+____=(x-____)2;
(3)x2+5x+____=(x+____)2;
(4)x2-
x+____=(x-____)2.
25
5
36
6
随堂练习
2
解:(1)移项,得x2-x=,
配方,得x2-x+
=
+
,
(x-
)2=2,
由此可得,x-
=±
,
x1=
+
,x2=
-
.
解下列方程:
(1)x2-x-
=0;
(2)x(x+4)=8x+12.
随堂练习
2
解下列方程:
(1)x2-x-
=0;
(2)x(x+4)=8x+12.
解:
(2)去括号,移项,合并同类项,得x2-4x=12,
配方,得x2-4x+4=12+4,(x-2)2=16,
由此可得x-2=±4,x1=6,x2=-2.
课堂小结
1.
通过配成完全平方的形式来解一元二次方程的方法,
叫做配方法.
2.
用配方法解一元二次方程的一般步骤:
一移
→
二化
→
三配→
四开.
对接中考
1
一元二次方程
配方后可化为(
)
A.
B.
C.
D.
B
对接中考
2
若将一元二次方程
x2-8x-9=0
化成
(x+n)2=d
的形式,则n=
,d=
.
-4
25
x2-8x-9=0,
x2-8x=9,
移项得
配方
x2-8x+
42
=9+
42
,
所以
(x-4)2=25,
即
n=-
4,d=25.
解:
对接中考
3
已知方程
x2-6x+q=0
配方后是
(x-p)2=7
,那么方程
x2+6x+q=0
配方后是(
)
A.(x-p)2=5
B.(x+p)2=5
C.(x-p)2=7
D.(x+p)2=7
D
同课章节目录
