第一章 一元一次不等式组总复习
图片预览




文档简介
(共11张PPT)
1、判断下列各式是否是一元一次不等式组
(1)X-1<0 (2) X-1<0 (3) X-1<0
Y>0 X>0
(4)X-1<0 (5) X-1<0
>0 X+1<0
X>0
问题与回顾
理解一元一次不等式组的概念注意:
1)在同一不等式组里的未知数必须是同一个;
2)不等式组里不等式的个数并未规定;
3)均为一元一次不等式。
×
×
√
×
√
2、列一元一次不等式组
X的相反数的2倍与3的和是非负数,且x与1的差不大于-4。
-2x+3≥0
x-1≤-4
列一元一次不等式组时注意:
1、抓住表示数量关系的关键词明确运算列出代数式。如:倍、和、差等
2、抓住表示不等关系的关键词明确不等关系列出不等式。如:大于、小于、不大于、不小于、非负数等。
3、解一元一次不等式组分几步完成?关键一步是什么?
第一步:分别解每一个不等式;
第二步:利用数轴找出所有解集的公共部分(一定是用不等式表示出来)。
★
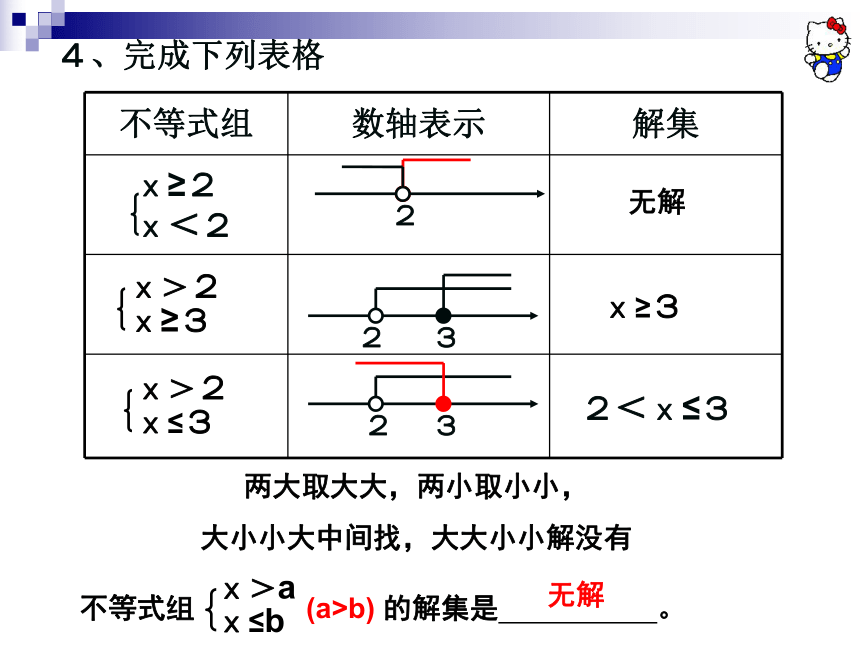
4、完成下列表格
不等式组 数轴表示 解集
x<2
x≥2
2
3
2<x≤3
2
无解
x>2
x≥3
x≥3
2
3
x>2
x≤3
两大取大大,两小取小小,
大小小大中间找,大大小小解没有
x>a
x≤b
不等式组 (a>b) 的解集是 。
无解
巩固与提升
例1(2007山东威海)解不等式组:
解:解不等式①得:x≥-2
解不等式②得:x<-
在数轴上表示不等式①、②的解集为
-2
所以不等式组的解集为-2≤x<-
0、1、2
2、(2007湖北咸宁)不等式组
的整数解是___________.
4、若不等式组 无解,
则m的取值范围是 。
m≤1
1、不等式组 的解集是 。
t=3
3、求不等式的 解集
解:原不等式可变为
解得:
应用与解决
例2、某县城规定每人每月用电量不超过50度部分按每度0.5元收费,超过部分按每度0.8元收费。已知小明家有5口人,每月总用电量超过50度,其电费预算支出为49~65元。你能知道小明家每月用电量应控制在什么范围内吗?
分析:
1、设小明家每月用电量为x度(x>50)
单价(元/度) 用电量(度) 电费(元)
规定部分
超过部分
0.5
0.8
50
X-50
0.5×50
0.8(x-50)
3、两个不等关系为:(题中直接指出)
2、总电费为:0.5×50+ 0.8(x-50)
4、列不等式组——解不等式组——根据实际确定答案
5、作答
解:设小明家每月用电量为x度(x>50),依题意得
0.5×50+ 0.8(x-50) ≥49
0.5×50+ 0.8(x-50) ≤65
①
②
解不等式①得 x≥80
解不等式②得 x≤100
所以不等式组的解集是 80≤x≤100
答:小明家的用电量应控制在80~100度之间。
3、有一群猴子,分桃子时若每只猴子分3个,则剩59个;若每只猴子分5个,都能分得桃子,但有一只猴子分得的桃子不够5个,问有多少只猴子多少个桃子?
分析:
1、设有x只猴子,
则桃子数为(3x+59)个
每只猴子5个, X只猴子需5x个桃子,超过已有桃子数;每只猴子5个,(X-1)只猴子需5(x-1)个桃子,少于已有桃子数。
或:每只猴子5个,(X-1)只猴子需5(x-1)个桃子,最后一只猴子分得的桃子数为:(3x+59)- 5(x-1),最后一只猴子不够5个:最后一只猴子分得的桃子数大于0而小于5。
2、不等关系
解:设有x只猴子,则桃子数为(3x+59)个,依题意得
5x> 3x+59
5(x-1)< 3x+59
解得:29.5<x<32
因为x为整数,所以x=30或x=31.
当x=30时,3x+59=149
当x=31时,3x+59=152
答:有30只猴子,149个桃子或有31只猴子,152个桃子。
2、机动:P13复习题一A组6T
(2007四川成都)解不等式组:
并写出该不等式组的整数解.
作业与检测
1、判断下列各式是否是一元一次不等式组
(1)X-1<0 (2) X-1<0 (3) X-1<0
Y>0 X>0
(4)X-1<0 (5) X-1<0
>0 X+1<0
X>0
问题与回顾
理解一元一次不等式组的概念注意:
1)在同一不等式组里的未知数必须是同一个;
2)不等式组里不等式的个数并未规定;
3)均为一元一次不等式。
×
×
√
×
√
2、列一元一次不等式组
X的相反数的2倍与3的和是非负数,且x与1的差不大于-4。
-2x+3≥0
x-1≤-4
列一元一次不等式组时注意:
1、抓住表示数量关系的关键词明确运算列出代数式。如:倍、和、差等
2、抓住表示不等关系的关键词明确不等关系列出不等式。如:大于、小于、不大于、不小于、非负数等。
3、解一元一次不等式组分几步完成?关键一步是什么?
第一步:分别解每一个不等式;
第二步:利用数轴找出所有解集的公共部分(一定是用不等式表示出来)。
★
4、完成下列表格
不等式组 数轴表示 解集
x<2
x≥2
2
3
2<x≤3
2
无解
x>2
x≥3
x≥3
2
3
x>2
x≤3
两大取大大,两小取小小,
大小小大中间找,大大小小解没有
x>a
x≤b
不等式组 (a>b) 的解集是 。
无解
巩固与提升
例1(2007山东威海)解不等式组:
解:解不等式①得:x≥-2
解不等式②得:x<-
在数轴上表示不等式①、②的解集为
-2
所以不等式组的解集为-2≤x<-
0、1、2
2、(2007湖北咸宁)不等式组
的整数解是___________.
4、若不等式组 无解,
则m的取值范围是 。
m≤1
1、不等式组 的解集是 。
t=3
3、求不等式的 解集
解:原不等式可变为
解得:
应用与解决
例2、某县城规定每人每月用电量不超过50度部分按每度0.5元收费,超过部分按每度0.8元收费。已知小明家有5口人,每月总用电量超过50度,其电费预算支出为49~65元。你能知道小明家每月用电量应控制在什么范围内吗?
分析:
1、设小明家每月用电量为x度(x>50)
单价(元/度) 用电量(度) 电费(元)
规定部分
超过部分
0.5
0.8
50
X-50
0.5×50
0.8(x-50)
3、两个不等关系为:(题中直接指出)
2、总电费为:0.5×50+ 0.8(x-50)
4、列不等式组——解不等式组——根据实际确定答案
5、作答
解:设小明家每月用电量为x度(x>50),依题意得
0.5×50+ 0.8(x-50) ≥49
0.5×50+ 0.8(x-50) ≤65
①
②
解不等式①得 x≥80
解不等式②得 x≤100
所以不等式组的解集是 80≤x≤100
答:小明家的用电量应控制在80~100度之间。
3、有一群猴子,分桃子时若每只猴子分3个,则剩59个;若每只猴子分5个,都能分得桃子,但有一只猴子分得的桃子不够5个,问有多少只猴子多少个桃子?
分析:
1、设有x只猴子,
则桃子数为(3x+59)个
每只猴子5个, X只猴子需5x个桃子,超过已有桃子数;每只猴子5个,(X-1)只猴子需5(x-1)个桃子,少于已有桃子数。
或:每只猴子5个,(X-1)只猴子需5(x-1)个桃子,最后一只猴子分得的桃子数为:(3x+59)- 5(x-1),最后一只猴子不够5个:最后一只猴子分得的桃子数大于0而小于5。
2、不等关系
解:设有x只猴子,则桃子数为(3x+59)个,依题意得
5x> 3x+59
5(x-1)< 3x+59
解得:29.5<x<32
因为x为整数,所以x=30或x=31.
当x=30时,3x+59=149
当x=31时,3x+59=152
答:有30只猴子,149个桃子或有31只猴子,152个桃子。
2、机动:P13复习题一A组6T
(2007四川成都)解不等式组:
并写出该不等式组的整数解.
作业与检测
