解直角三角形的应用(复习课)
文档属性
| 名称 | 解直角三角形的应用(复习课) |  | |
| 格式 | rar | ||
| 文件大小 | 830.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-02 15:06:00 | ||
图片预览


文档简介
(共14张PPT)
---解直角三角形的应用
教学目标:
1、使学生学过的知识条理化、系统化,同时通过复习
找出平时的缺、漏,以便及时弥补.
2、培养学生综合、概括等逻辑思维能力及分析问题、解
决问题的能力.
3.德育渗透点
教学重点:
锐角三角函数的概念、特殊角的三角函数值、
余角余函数关系、
同角三角函数关系、查表等知识及简单应用.
教学难点:
知识的应用.
A
B
C
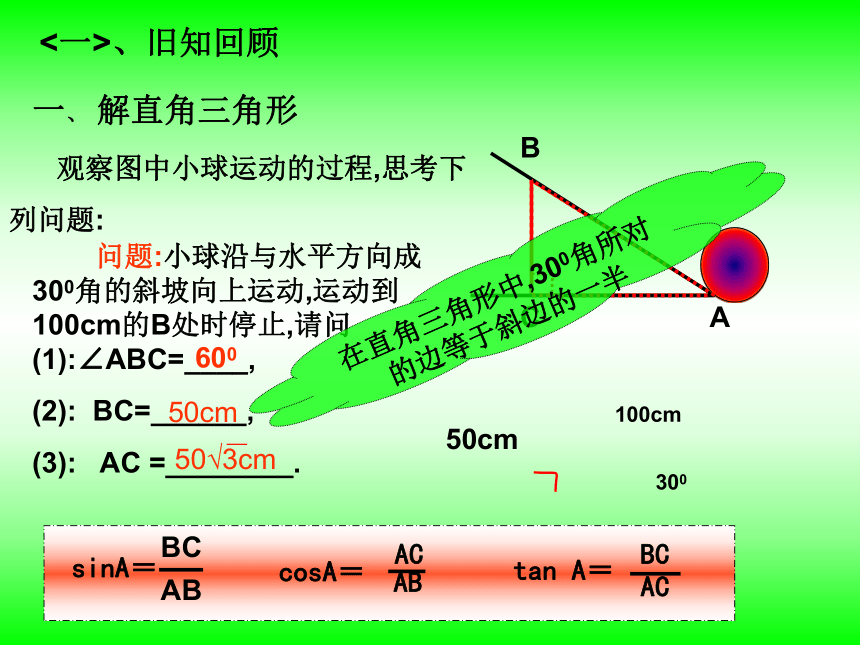
一、 解直角三角形
问题:小球沿与水平方向成300角的斜坡向上运动,运动到100cm的B处时停止,请问 (1):∠ABC=____,
(2): BC=______,
(3): AC =________.
观察图中小球运动的过程,思考下
列问题:
<一>、旧知回顾
600
50cm
50√3cm
100cm
300
50cm
在直角三角形中,300角所对的边等于斜边的一半
sinA=
BC
AB
cosA=
AC
AB
tan A=
BC
AC
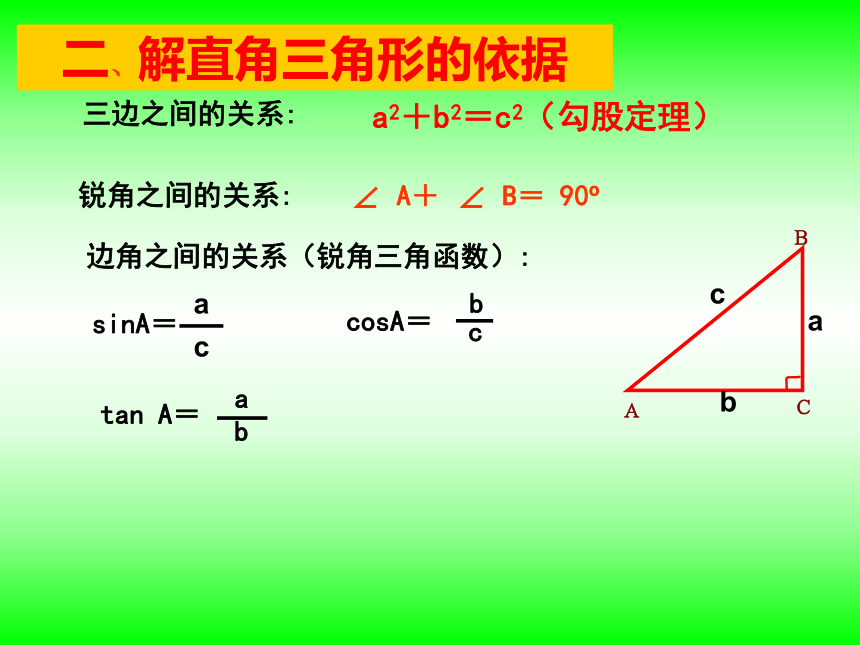
三边之间的关系:
a2+b2=c2(勾股定理)
锐角之间的关系:
∠ A+ ∠ B= 90
边角之间的关系(锐角三角函数):
tan A=
a
b
sinA=
a
c
cosA=
b
c
A
C
B
a
b
c
二、解直角三角形的依据
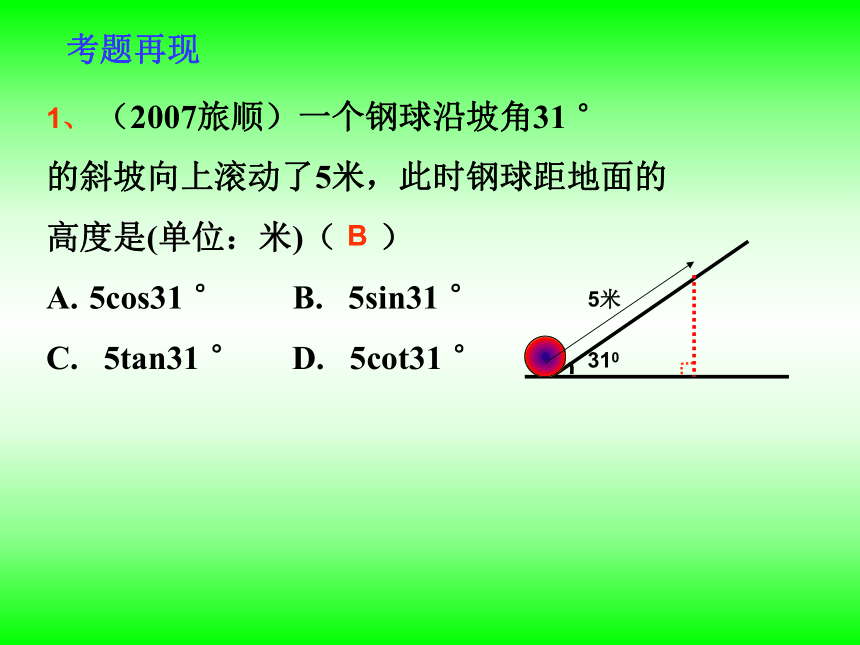
1、 (2007旅顺)一个钢球沿坡角31 °
的斜坡向上滚动了5米,此时钢球距地面的
高度是(单位:米)( )
5cos31 ° B. 5sin31 °
C. 5tan31 ° D. 5cot31 °
考题再现
B
310
5米
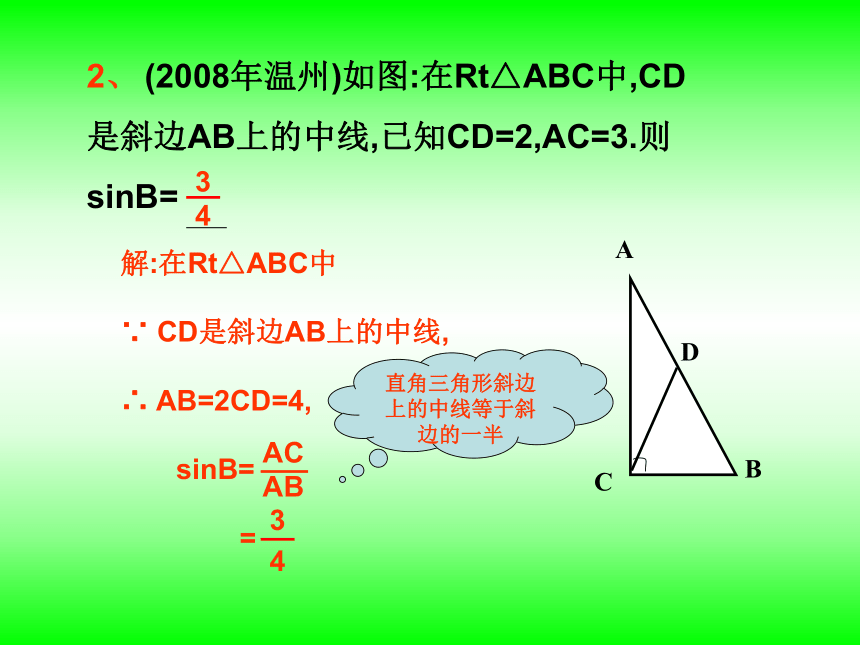
2、 (2008年温州)如图:在Rt△ABC中,CD
是斜边AB上的中线,已知CD=2,AC=3.则
sinB=
解:在Rt△ABC中
∵ CD是斜边AB上的中线,
∴ AB=2CD=4,
sinB=
=
AC
AB
3
4
A
B
C
D
3
4
直角三角形斜边上的中线等于斜边的一半
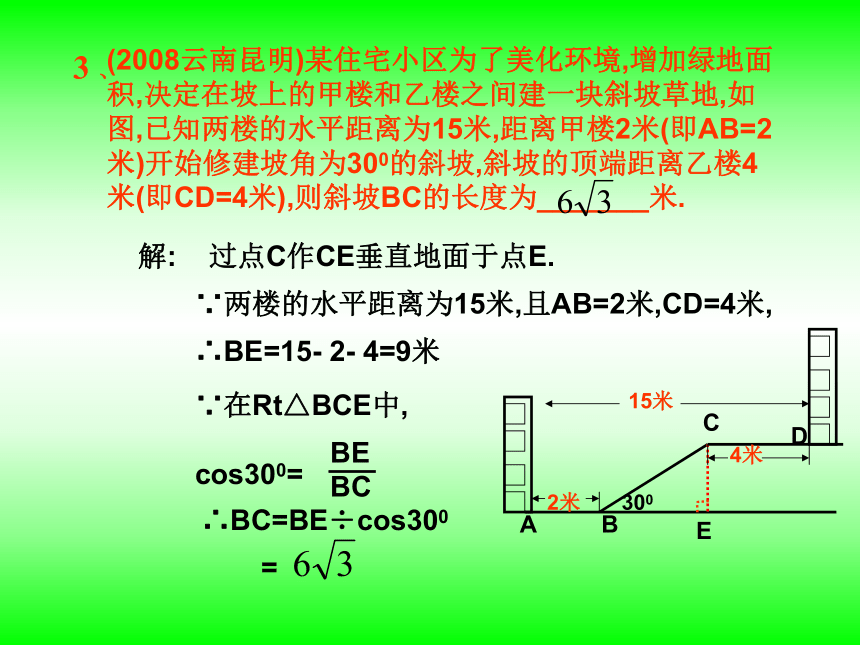
3 、
(2008云南昆明)某住宅小区为了美化环境,增加绿地面积,决定在坡上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为300的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),则斜坡BC的长度为_______米.
300
C
D
A
B
E
解: 过点C作CE垂直地面于点E.
∵两楼的水平距离为15米,且AB=2米,CD=4米,
∴BE=15- 2- 4=9米
∵在Rt△BCE中,
cos300=
∴BC=BE÷cos300
BE
BC
=
15米
2米
4米
在解直角三角形及应用时经常接触到的一些概念
<三>、基本概念
(1)仰角和俯角:
(2)方位角:
30°
45°
B
O
A
东
西
北
南
水平线
铅垂线
仰角
俯角
视线
视线
(2007南充)如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,则A,C两地的距离为 ____
北
A
北
B
C
400
40海里
D
200
有一个角是600的三角形是等边三角形
答:货轮无触礁危险。
在Rt△ADC中,
∵ tan∠DCA=------
∴AD= tan600x= x
在Rt△ADB中,
∵ tan30 = ---- = --------
AD≈12×1.732 =20.784 > 20
解:过点A作AD⊥BC于D,
A
B
D
C
N
N1
30
60
二、例题赏析
24海里
X
AD
DC
AD
BD
3 x
√
X=12
X+24
设CD=x,则BD=X+24
例、(2006贵州)如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 ,航行24海里到C,见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
30
60
(2007年昆明)如图,AB和CD是同一地面上的两座相距36米的楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为450,楼底D的俯角为300,求楼CD的高?(结果保留根号)
300
450
A
B
C
D
36
2、本节学习以后,我们可以得到解直角三角形的两种基本图形:
小结:
A
A
B
B
C
C
D
D
1、解直角三角形的依据.
三边之间的关系:
a2+b2=c2(勾股定理);
锐角之间的关系:
∠ A+ ∠ B= 90
边角之间的关系(锐角三角函数):
sinA=
a
c
cosA=
b
c
tan A=
a
b
A
C
B
a
b
c
(2007淄博)王英同学从A地沿北偏西60 方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地多少距离?
A
B
C
北
南
西
东
D
E
600
100m
200m
---解直角三角形的应用
教学目标:
1、使学生学过的知识条理化、系统化,同时通过复习
找出平时的缺、漏,以便及时弥补.
2、培养学生综合、概括等逻辑思维能力及分析问题、解
决问题的能力.
3.德育渗透点
教学重点:
锐角三角函数的概念、特殊角的三角函数值、
余角余函数关系、
同角三角函数关系、查表等知识及简单应用.
教学难点:
知识的应用.
A
B
C
一、 解直角三角形
问题:小球沿与水平方向成300角的斜坡向上运动,运动到100cm的B处时停止,请问 (1):∠ABC=____,
(2): BC=______,
(3): AC =________.
观察图中小球运动的过程,思考下
列问题:
<一>、旧知回顾
600
50cm
50√3cm
100cm
300
50cm
在直角三角形中,300角所对的边等于斜边的一半
sinA=
BC
AB
cosA=
AC
AB
tan A=
BC
AC
三边之间的关系:
a2+b2=c2(勾股定理)
锐角之间的关系:
∠ A+ ∠ B= 90
边角之间的关系(锐角三角函数):
tan A=
a
b
sinA=
a
c
cosA=
b
c
A
C
B
a
b
c
二、解直角三角形的依据
1、 (2007旅顺)一个钢球沿坡角31 °
的斜坡向上滚动了5米,此时钢球距地面的
高度是(单位:米)( )
5cos31 ° B. 5sin31 °
C. 5tan31 ° D. 5cot31 °
考题再现
B
310
5米
2、 (2008年温州)如图:在Rt△ABC中,CD
是斜边AB上的中线,已知CD=2,AC=3.则
sinB=
解:在Rt△ABC中
∵ CD是斜边AB上的中线,
∴ AB=2CD=4,
sinB=
=
AC
AB
3
4
A
B
C
D
3
4
直角三角形斜边上的中线等于斜边的一半
3 、
(2008云南昆明)某住宅小区为了美化环境,增加绿地面积,决定在坡上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为300的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),则斜坡BC的长度为_______米.
300
C
D
A
B
E
解: 过点C作CE垂直地面于点E.
∵两楼的水平距离为15米,且AB=2米,CD=4米,
∴BE=15- 2- 4=9米
∵在Rt△BCE中,
cos300=
∴BC=BE÷cos300
BE
BC
=
15米
2米
4米
在解直角三角形及应用时经常接触到的一些概念
<三>、基本概念
(1)仰角和俯角:
(2)方位角:
30°
45°
B
O
A
东
西
北
南
水平线
铅垂线
仰角
俯角
视线
视线
(2007南充)如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,则A,C两地的距离为 ____
北
A
北
B
C
400
40海里
D
200
有一个角是600的三角形是等边三角形
答:货轮无触礁危险。
在Rt△ADC中,
∵ tan∠DCA=------
∴AD= tan600x= x
在Rt△ADB中,
∵ tan30 = ---- = --------
AD≈12×1.732 =20.784 > 20
解:过点A作AD⊥BC于D,
A
B
D
C
N
N1
30
60
二、例题赏析
24海里
X
AD
DC
AD
BD
3 x
√
X=12
X+24
设CD=x,则BD=X+24
例、(2006贵州)如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 ,航行24海里到C,见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
30
60
(2007年昆明)如图,AB和CD是同一地面上的两座相距36米的楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为450,楼底D的俯角为300,求楼CD的高?(结果保留根号)
300
450
A
B
C
D
36
2、本节学习以后,我们可以得到解直角三角形的两种基本图形:
小结:
A
A
B
B
C
C
D
D
1、解直角三角形的依据.
三边之间的关系:
a2+b2=c2(勾股定理);
锐角之间的关系:
∠ A+ ∠ B= 90
边角之间的关系(锐角三角函数):
sinA=
a
c
cosA=
b
c
tan A=
a
b
A
C
B
a
b
c
(2007淄博)王英同学从A地沿北偏西60 方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地多少距离?
A
B
C
北
南
西
东
D
E
600
100m
200m
