六年级下册数学课件-《4、正比例和反比例练习》(1) 苏教版 (共19张PPT)
文档属性
| 名称 | 六年级下册数学课件-《4、正比例和反比例练习》(1) 苏教版 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 614.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 17:53:47 | ||
图片预览






文档简介
(共19张PPT)
用比例列方程解决实际问题
1、判断下面两种相关联的量成什么比例?正比例请举红旗;反比例请举黄旗。
(1)速度一定,路程和时间成(
)比例。
(2)路程一定,速度和时间成( )比例。
(3)订阅《小学生数学报》,订阅数量和订阅总价成( )比例。
(4)一辆汽车从甲地驶入乙地,行驶的速度和时间成( )比例。
正
反
正
反
创设情境,唤醒原型
思考:1、这道题中涉及哪三种量?
2、哪种量是一定?
3、总价和数量成什么比例关系?
总价、数量和单价。
单价一定。
单价一定,总价和数量成正比例。
例1:小明买6本笔记本用了30元,小刚想买4本同样的笔记本,要用多少钱?
创设情境,唤醒原型
例1:小明买6本笔记本用了30元,小刚想买4本同样的笔记本,要用多少钱?
创设情境,唤醒原型
要求:
①直接用比例列方程解答;
②有困难的可以跟老师示意,求助智慧锦囊;
③思考:这样列式的理由是什么?
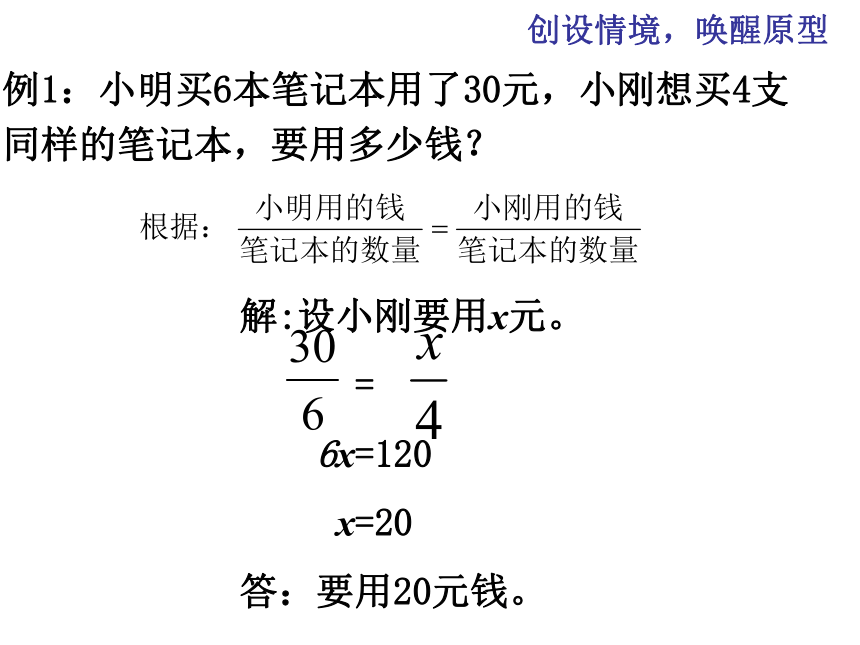
例1:小明买6本笔记本用了30元,小刚想买4本同样的笔记本,要用多少钱?
创设情境,唤醒原型
例1:小明买6本笔记本用了30元,小刚想买4支同样的笔记本,要用多少钱?
解:设小刚要用x元。
=
6x=120
x=20
答:要用20元钱。
创设情境,唤醒原型
(1)找出题目中的相关联的量;
(2)判断题目中两种相关联的量是成哪种比例关系;
(3)设未知量为x;
(4)列出方程并解答;
(5)检验后写出答案;
用比例列方程解决实际问题的步骤:
自主尝试,建设模型
例2:一辆汽车从甲地开往乙地,如果每小时行驶80千米,需要行驶9小时;如果每小时行驶90千米,那么需要行驶几小时?
解:设需要行驶x小时。
90x=80×9
90x=720
x=8
答:需要行驶8小时。
自主尝试,建设模型
1.张大妈家上个月用了8吨水,水费是12.8元;李奶奶家用了10吨水,李奶奶家上个月的水费是x元。
只列方程不计算:
2.一个办公楼原来平均每天照明用电100千瓦时,改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用x天。
25x=100×5
抽象本质,优化模型
3.甲乙两车从相距272千米的两地同时相向而行,3小时后两车还相距17千米。甲每小时行驶45千米,乙每小时行驶多少千米?
抽象本质,优化模型
解:设乙每小时行驶x千米。
45×3+3x+17=272
3x=120
x=40
答:乙每小时行驶40千米。
(1)找出题目中的等量关系;
(2)设未知量为x;
(3)列出方程并解答;
(4)检验后写出答案;
列方程解决问题的步骤:
抽象本质,优化模型
用比例解决问题的步骤:
(1)找出题目中的正反比例关系;
(2)设未知量为x;
(3)列出方程并解答;
(4)检验后写出答案;
某加工厂做一批零件,若每天加工200个,20天可以完成;若每天多加工50个,需几天完成?(用比例解)
解:设需x天完成。
(200+50)x=200×20
250x=4000
x
=16
答:需16天完成。
抽象本质,优化模型
某农场要收割小麦140公顷,前3天收割了84公顷,照这样计算,剩下的还要几天才能收割完?(用比例解)
解:设剩下的x天才能收完
(140-84):x
=84
:
3
84x=168
x=2
答:剩下的还要2天才能收割完。
公项数
:
时间
=
每天收割的公顷数(一定)
抽象本质,优化模型
必做题:
工程队修一条水渠,每天工作6小时,12天可以完成。如果工作效率不变,每天工作8小时,多少天可以完成任务?(用比例解)
解:设x天可以完成任务。
8x=6×12
8x=72
x=9
答:9天可以完成任务。
深化运用,衍生模型
选做题:
☆:从甲地开往乙地,客车要10小时,货车要15小时,货车与客车的速度比是(
)。
A.3:2
B.2:3
C.3:5
D无法确定
☆☆:用同样的砖铺地,铺边长6分米的方砖要用128块。如果改铺边长8分米的方砖,需要多少块?(用比例解)
☆☆☆:合理选条件,帮助他编题。
小明受老师委托,编一道比例应用题,于是他前往“数学超市”选购了一些条件:①计划每天生产30辆;②实际每天生产40辆;③计划25天完成;④实际20天完成;⑤计划一共生产了900辆;⑥实际一共生产了1000辆。
小明需要你的帮助,你能帮助他编编题吗?写出你编的问题。
深化运用,衍生模型
选做题:
☆:从甲地开往乙地,客车要10小时,货车要15小时,货车与客车的速度比是(
)。
A.3:2
B.2:3
C.3:5
D无法确定
深化运用,衍生模型
B
选做题:
☆☆:用同样的砖铺地,铺边长6分米的方砖要用128块。如果改铺边长8分米的方砖,需要多少块?(用比例知识解)
深化运用,衍生模型
解:设需要x块方砖。
128×6?=x×8?
64x=4608
x=72
答:需要72块方砖。
选做题:
☆☆☆:合理选条件,帮助他编题。
小明受老师委托,编一道比例应用题,于是他前往“数学超市”选购了一些条件:①计划每天生产30辆;
②实际每天生产40辆;
③计划25天完成;
④实际20天完成;
⑤计划一共生产了900辆;
⑥实际一共生产了1000辆。
小明需要你的帮助,你能帮助他编编题吗?写出你编的问题。
深化运用,衍生模型
★用比例解决问题时需要哪几个步骤?
1、找
2、判
3、设
4、列
5、检
用比例列方程解决实际问题
1、判断下面两种相关联的量成什么比例?正比例请举红旗;反比例请举黄旗。
(1)速度一定,路程和时间成(
)比例。
(2)路程一定,速度和时间成( )比例。
(3)订阅《小学生数学报》,订阅数量和订阅总价成( )比例。
(4)一辆汽车从甲地驶入乙地,行驶的速度和时间成( )比例。
正
反
正
反
创设情境,唤醒原型
思考:1、这道题中涉及哪三种量?
2、哪种量是一定?
3、总价和数量成什么比例关系?
总价、数量和单价。
单价一定。
单价一定,总价和数量成正比例。
例1:小明买6本笔记本用了30元,小刚想买4本同样的笔记本,要用多少钱?
创设情境,唤醒原型
例1:小明买6本笔记本用了30元,小刚想买4本同样的笔记本,要用多少钱?
创设情境,唤醒原型
要求:
①直接用比例列方程解答;
②有困难的可以跟老师示意,求助智慧锦囊;
③思考:这样列式的理由是什么?
例1:小明买6本笔记本用了30元,小刚想买4本同样的笔记本,要用多少钱?
创设情境,唤醒原型
例1:小明买6本笔记本用了30元,小刚想买4支同样的笔记本,要用多少钱?
解:设小刚要用x元。
=
6x=120
x=20
答:要用20元钱。
创设情境,唤醒原型
(1)找出题目中的相关联的量;
(2)判断题目中两种相关联的量是成哪种比例关系;
(3)设未知量为x;
(4)列出方程并解答;
(5)检验后写出答案;
用比例列方程解决实际问题的步骤:
自主尝试,建设模型
例2:一辆汽车从甲地开往乙地,如果每小时行驶80千米,需要行驶9小时;如果每小时行驶90千米,那么需要行驶几小时?
解:设需要行驶x小时。
90x=80×9
90x=720
x=8
答:需要行驶8小时。
自主尝试,建设模型
1.张大妈家上个月用了8吨水,水费是12.8元;李奶奶家用了10吨水,李奶奶家上个月的水费是x元。
只列方程不计算:
2.一个办公楼原来平均每天照明用电100千瓦时,改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用x天。
25x=100×5
抽象本质,优化模型
3.甲乙两车从相距272千米的两地同时相向而行,3小时后两车还相距17千米。甲每小时行驶45千米,乙每小时行驶多少千米?
抽象本质,优化模型
解:设乙每小时行驶x千米。
45×3+3x+17=272
3x=120
x=40
答:乙每小时行驶40千米。
(1)找出题目中的等量关系;
(2)设未知量为x;
(3)列出方程并解答;
(4)检验后写出答案;
列方程解决问题的步骤:
抽象本质,优化模型
用比例解决问题的步骤:
(1)找出题目中的正反比例关系;
(2)设未知量为x;
(3)列出方程并解答;
(4)检验后写出答案;
某加工厂做一批零件,若每天加工200个,20天可以完成;若每天多加工50个,需几天完成?(用比例解)
解:设需x天完成。
(200+50)x=200×20
250x=4000
x
=16
答:需16天完成。
抽象本质,优化模型
某农场要收割小麦140公顷,前3天收割了84公顷,照这样计算,剩下的还要几天才能收割完?(用比例解)
解:设剩下的x天才能收完
(140-84):x
=84
:
3
84x=168
x=2
答:剩下的还要2天才能收割完。
公项数
:
时间
=
每天收割的公顷数(一定)
抽象本质,优化模型
必做题:
工程队修一条水渠,每天工作6小时,12天可以完成。如果工作效率不变,每天工作8小时,多少天可以完成任务?(用比例解)
解:设x天可以完成任务。
8x=6×12
8x=72
x=9
答:9天可以完成任务。
深化运用,衍生模型
选做题:
☆:从甲地开往乙地,客车要10小时,货车要15小时,货车与客车的速度比是(
)。
A.3:2
B.2:3
C.3:5
D无法确定
☆☆:用同样的砖铺地,铺边长6分米的方砖要用128块。如果改铺边长8分米的方砖,需要多少块?(用比例解)
☆☆☆:合理选条件,帮助他编题。
小明受老师委托,编一道比例应用题,于是他前往“数学超市”选购了一些条件:①计划每天生产30辆;②实际每天生产40辆;③计划25天完成;④实际20天完成;⑤计划一共生产了900辆;⑥实际一共生产了1000辆。
小明需要你的帮助,你能帮助他编编题吗?写出你编的问题。
深化运用,衍生模型
选做题:
☆:从甲地开往乙地,客车要10小时,货车要15小时,货车与客车的速度比是(
)。
A.3:2
B.2:3
C.3:5
D无法确定
深化运用,衍生模型
B
选做题:
☆☆:用同样的砖铺地,铺边长6分米的方砖要用128块。如果改铺边长8分米的方砖,需要多少块?(用比例知识解)
深化运用,衍生模型
解:设需要x块方砖。
128×6?=x×8?
64x=4608
x=72
答:需要72块方砖。
选做题:
☆☆☆:合理选条件,帮助他编题。
小明受老师委托,编一道比例应用题,于是他前往“数学超市”选购了一些条件:①计划每天生产30辆;
②实际每天生产40辆;
③计划25天完成;
④实际20天完成;
⑤计划一共生产了900辆;
⑥实际一共生产了1000辆。
小明需要你的帮助,你能帮助他编编题吗?写出你编的问题。
深化运用,衍生模型
★用比例解决问题时需要哪几个步骤?
1、找
2、判
3、设
4、列
5、检
