六年级下册数学课件 《4、正比例和反比例练习》(2) 苏教版 (共29张PPT)
文档属性
| 名称 | 六年级下册数学课件 《4、正比例和反比例练习》(2) 苏教版 (共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
《正比例的意义》自主学习单
一、自主学习第56页例1,回答以下问题:
1、表中列出了哪两种量?
2、观察表中的数据,说一说,哪一种量的变化引起了另外一种量的变化?
3、仔细观察表中的数据,这两种量在变化中有没有不变的规律?
写出几组相对应的路程和时间的比,并求出比值。这个比值表示什么?
4、这个规律能否用一个式子表示?
路程和时间
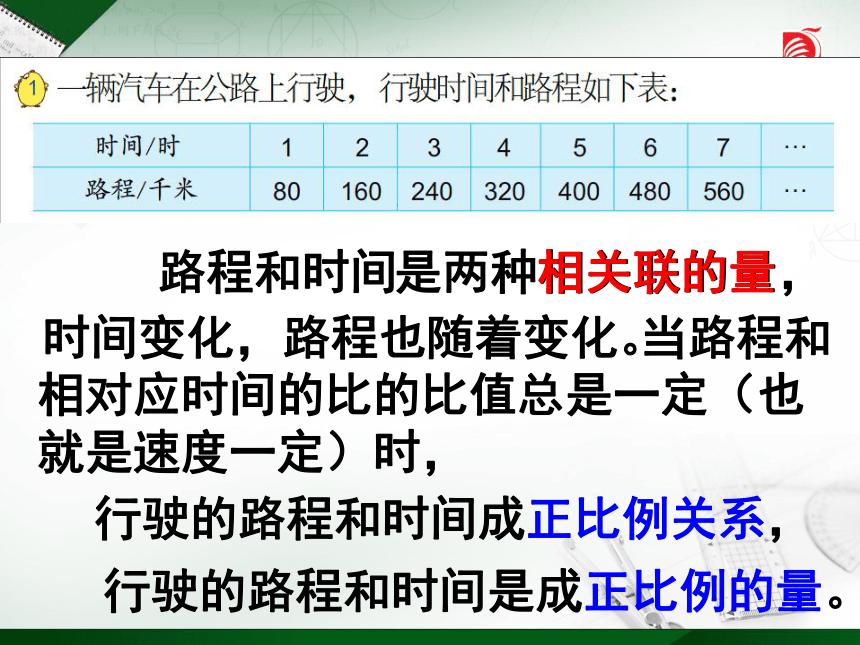
是两种相关联的量,
时间变化,路程也随着变化。
当路程和相对应时间的比的比值总是一定(也就是速度一定)时,
行驶的路程和时间成正比例关系,
行驶的路程和时间是成正比例的量。
相关联的量
路程和时间
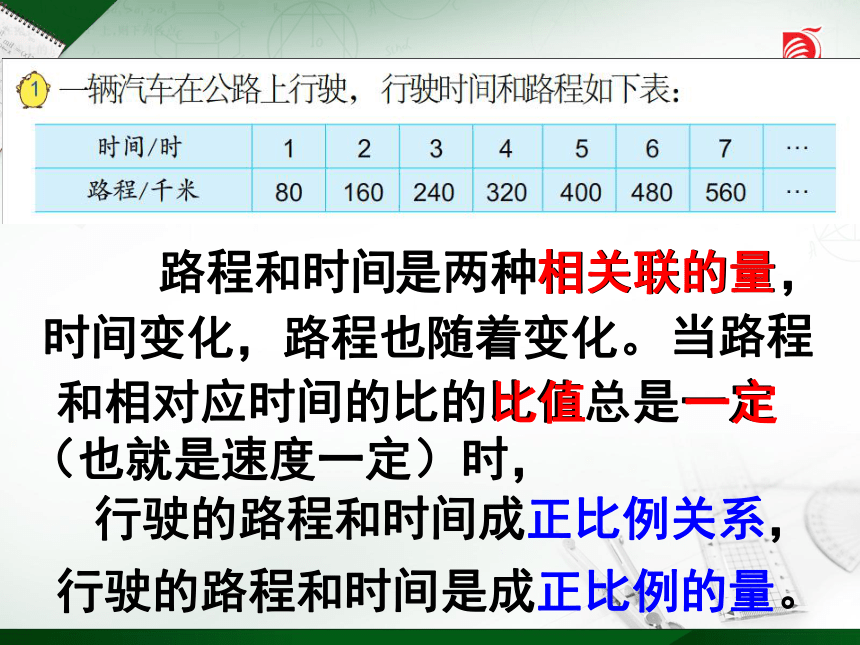
是两种相关联的量,
时间变化,路程也随着变化。
当路程
和相对应时间的比的比值总是一定
(也就是速度一定)时,
行驶的路程和时间成正比例关系,
行驶的路程和时间是成正比例的量。
相关联的量
比值
一定
1.6
2
2.4
自学提示:
(1)填一填,说一说总价和数量的变化。
(2)算一算,总价和对应数量的比值大小相等吗?
(3)写一写,你能用式子表示总价和对应数量的关系吗?
(4)判一判,铅笔的总价和数量成正比例吗?为什么?
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用下面的式子表示:
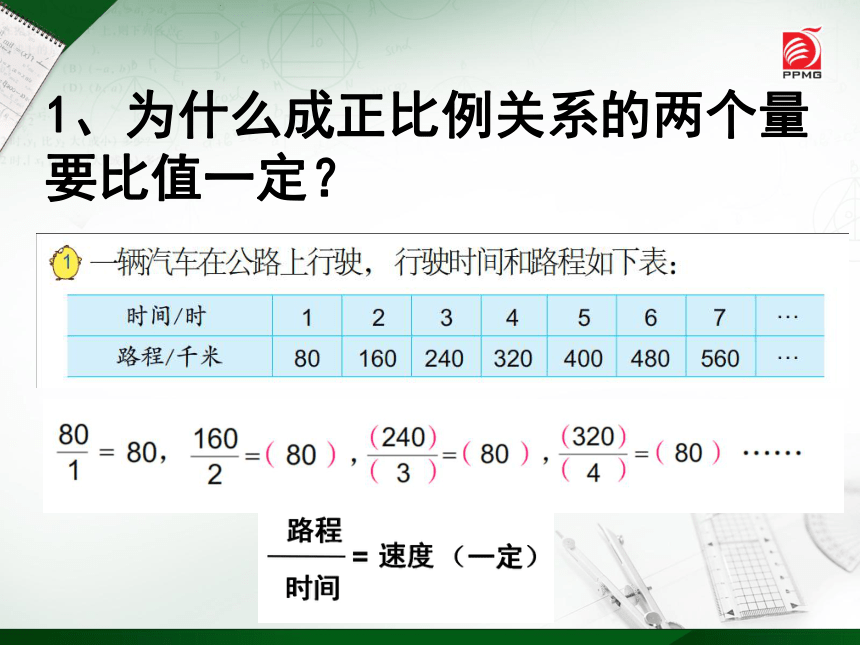
1、为什么成正比例关系的两个量要比值一定?
2、如果比值用
能否说明时间与路程是正比例关系?
3、生活中有没有反比例关系?
4、在初中是否还要学习正比例关系?
1、为什么成正比例关系的两个量要比值一定?
2、如果比值用
能否说明时间与路程是正比例关系?
每千米用的时间(一定)
正比例关系描述:
1、两种相关联的量,一种量扩大或缩小,另外一种量也随着扩大或缩小。
2、两种量相对应比的比值一定。
3、生活中有没有反比例关系?
1、两种相关联的量,一种量扩大或缩小,另外一种量也随着
缩小或扩大。
2、两种量(
)一定。
反比例关系描述
的积
4、在初中是否学习正比例关系?
活动1
南山湖水库水位的高低与相应的蓄水量如下表:
从表格中你能获取什么信息?你怎样读取表格中的信息?
横看:蓄水量随水位的变化而变化
竖看:对于水位的每一个值,蓄水量都有唯一值与它对应
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
如图,搭1条小鱼需要8根火柴棒,搭2条小鱼需要14根火柴棒,搭3条小鱼需要20根火柴棒,
(1)火柴棒根数s随着小鱼条数n的变化而变化
活动2
6n+2
1.这个变化过程中有哪些变量?
3.在这个变化过程中,两个变量有什么关系?
2.按这样的规律搭n条小鱼需要s根火柴棒,那么它们之间的关系s=
。
(2)对于小鱼条数n的每一个值,火柴棒根数s都有唯一值与它对应。
活动3
一石激起千层浪,小石子激起的波纹可以看作是一个不断向外扩展的圆.
(1)在这个变化过程中,有哪些变量?
(2)选择其中的两个,说说它们的关系.
圆的半径、直径、周长、面积…
一般地,如果在一个变化的过程中有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称
y是x的函数,x是自变量.
函数的概念
上海
南京
在这个变化过程中,有哪些函数?
1.把一根2m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为多少米?
(2)当长方形的宽为0.2m时,长为多少米?
(3)这个长方形的长是宽的函数吗?为什么?
(4)这个变化过程中还有其它函数吗?
解:(3)在这个变化过程中有两个变量“长”
和“宽”;“长”随着“宽”的变化而变化;且对于“宽”的每一个值,“长”都有唯一确定的值与之对应.
所以长方形的长是宽的函数.
2.按图示的运算程序,每输入一个实数
x
,便可输出一个相应的实数
y
.
小结
在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.
什么叫函数?
2、函数的表示方法
可以用三种方法
①图象法、
②列表法、
③解析式法
正比例函数定义
y=
kx是x的正比例函数
例1:下列函数关系式中,哪些是正比例函数?
正比例函数的表示方式
2、y=8x
y=x
y
3
0
-2
-1
0
1
2
x
…
-2
-1
0
1
2
…
y=x
…
…
漏刻是我国古代发明的一种计时工具,它是劳动人民的智慧结晶,也是一次函数的一次创造性地使用.请读一读教材课后阅读资料或上网查阅相关材料.
老师告诉你:
日落月出花果香,物转星移看沧桑。
?因果变化多联系,安得良策破迷茫?
?常变奠基说严谨,新知函数叙苍黄。
?相关变量有两个,对应唯一莫相忘。
《函数》
函数小史
我国清代数学家李善兰(1811-1882年)
在翻译《代数学》一书时,
把“function”译成“函数”沿用至今。
知识拓展——(见平台上的微课)
《正比例的意义》自主学习单
一、自主学习第56页例1,回答以下问题:
1、表中列出了哪两种量?
2、观察表中的数据,说一说,哪一种量的变化引起了另外一种量的变化?
3、仔细观察表中的数据,这两种量在变化中有没有不变的规律?
写出几组相对应的路程和时间的比,并求出比值。这个比值表示什么?
4、这个规律能否用一个式子表示?
路程和时间
是两种相关联的量,
时间变化,路程也随着变化。
当路程和相对应时间的比的比值总是一定(也就是速度一定)时,
行驶的路程和时间成正比例关系,
行驶的路程和时间是成正比例的量。
相关联的量
路程和时间
是两种相关联的量,
时间变化,路程也随着变化。
当路程
和相对应时间的比的比值总是一定
(也就是速度一定)时,
行驶的路程和时间成正比例关系,
行驶的路程和时间是成正比例的量。
相关联的量
比值
一定
1.6
2
2.4
自学提示:
(1)填一填,说一说总价和数量的变化。
(2)算一算,总价和对应数量的比值大小相等吗?
(3)写一写,你能用式子表示总价和对应数量的关系吗?
(4)判一判,铅笔的总价和数量成正比例吗?为什么?
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用下面的式子表示:
1、为什么成正比例关系的两个量要比值一定?
2、如果比值用
能否说明时间与路程是正比例关系?
3、生活中有没有反比例关系?
4、在初中是否还要学习正比例关系?
1、为什么成正比例关系的两个量要比值一定?
2、如果比值用
能否说明时间与路程是正比例关系?
每千米用的时间(一定)
正比例关系描述:
1、两种相关联的量,一种量扩大或缩小,另外一种量也随着扩大或缩小。
2、两种量相对应比的比值一定。
3、生活中有没有反比例关系?
1、两种相关联的量,一种量扩大或缩小,另外一种量也随着
缩小或扩大。
2、两种量(
)一定。
反比例关系描述
的积
4、在初中是否学习正比例关系?
活动1
南山湖水库水位的高低与相应的蓄水量如下表:
从表格中你能获取什么信息?你怎样读取表格中的信息?
横看:蓄水量随水位的变化而变化
竖看:对于水位的每一个值,蓄水量都有唯一值与它对应
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
如图,搭1条小鱼需要8根火柴棒,搭2条小鱼需要14根火柴棒,搭3条小鱼需要20根火柴棒,
(1)火柴棒根数s随着小鱼条数n的变化而变化
活动2
6n+2
1.这个变化过程中有哪些变量?
3.在这个变化过程中,两个变量有什么关系?
2.按这样的规律搭n条小鱼需要s根火柴棒,那么它们之间的关系s=
。
(2)对于小鱼条数n的每一个值,火柴棒根数s都有唯一值与它对应。
活动3
一石激起千层浪,小石子激起的波纹可以看作是一个不断向外扩展的圆.
(1)在这个变化过程中,有哪些变量?
(2)选择其中的两个,说说它们的关系.
圆的半径、直径、周长、面积…
一般地,如果在一个变化的过程中有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称
y是x的函数,x是自变量.
函数的概念
上海
南京
在这个变化过程中,有哪些函数?
1.把一根2m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为多少米?
(2)当长方形的宽为0.2m时,长为多少米?
(3)这个长方形的长是宽的函数吗?为什么?
(4)这个变化过程中还有其它函数吗?
解:(3)在这个变化过程中有两个变量“长”
和“宽”;“长”随着“宽”的变化而变化;且对于“宽”的每一个值,“长”都有唯一确定的值与之对应.
所以长方形的长是宽的函数.
2.按图示的运算程序,每输入一个实数
x
,便可输出一个相应的实数
y
.
小结
在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.
什么叫函数?
2、函数的表示方法
可以用三种方法
①图象法、
②列表法、
③解析式法
正比例函数定义
y=
kx是x的正比例函数
例1:下列函数关系式中,哪些是正比例函数?
正比例函数的表示方式
2、y=8x
y=x
y
3
0
-2
-1
0
1
2
x
…
-2
-1
0
1
2
…
y=x
…
…
漏刻是我国古代发明的一种计时工具,它是劳动人民的智慧结晶,也是一次函数的一次创造性地使用.请读一读教材课后阅读资料或上网查阅相关材料.
老师告诉你:
日落月出花果香,物转星移看沧桑。
?因果变化多联系,安得良策破迷茫?
?常变奠基说严谨,新知函数叙苍黄。
?相关变量有两个,对应唯一莫相忘。
《函数》
函数小史
我国清代数学家李善兰(1811-1882年)
在翻译《代数学》一书时,
把“function”译成“函数”沿用至今。
知识拓展——(见平台上的微课)
