六年级下册数学课件《6、立体图形的表面积和体积(1)》(4) 苏教版 (共61张PPT)
文档属性
| 名称 | 六年级下册数学课件《6、立体图形的表面积和体积(1)》(4) 苏教版 (共61张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 18:06:17 | ||
图片预览




文档简介
(共61张PPT)
学习目标:
1.我要进一步理解立体图形的表面积和体积(容积)的意义;
2.我要进一步掌握常用的体积(容积)单位及其进率,会进行它们之间的简单换算;
3.我要进一步掌握立体图形表面积和体积的计算方法,并能解决相关的实际问题。
导学单:
小组整理讨论:
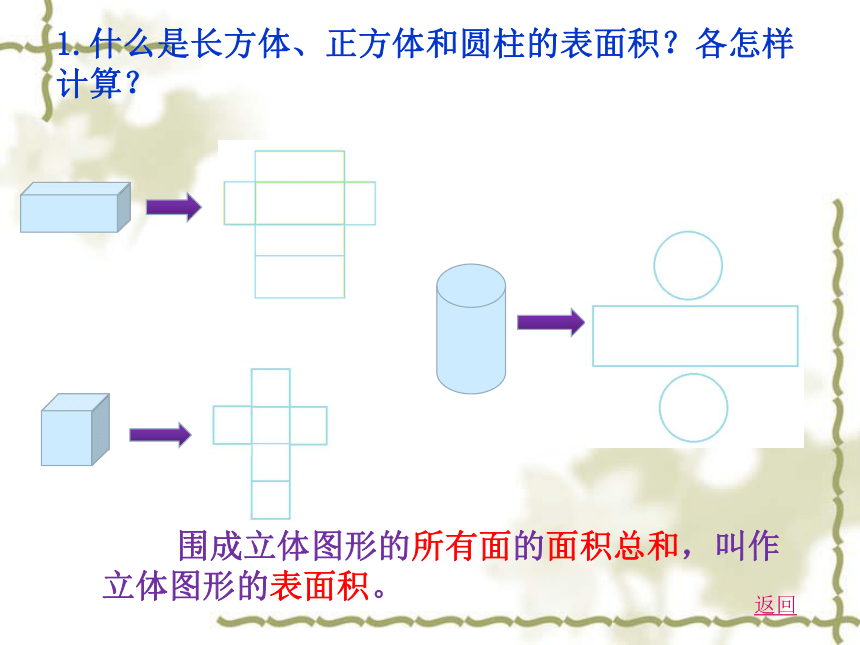
1.什么是长方体、正方体和圆柱的表面积?各怎样计算?
2.什么是物体的体积?什么是容器的容积?
3.常用的体积(容积)单位有哪些?相邻体积(容积)单位间的进率各是多少?
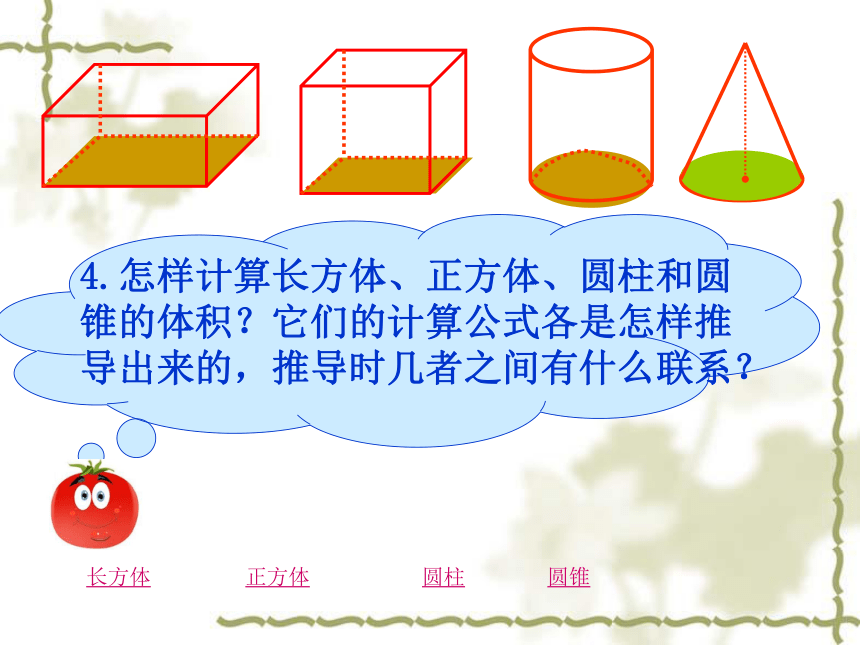
4.怎样计算长方体、正方体、圆柱和圆锥的体积?它们的计算公式各是怎样推导出来的,推导时几者之间有什么联系?
1.什么是长方体、正方体和圆柱的表面积?各怎样计算?
围成立体图形的所有面的面积总和,叫作立体图形的表面积。
返回
2.什么是物体的体积?什么是容器的容积?
物体所占空间的大小叫作物体的体积。
容器所能容纳物体的体积叫作容器的容积。
返回
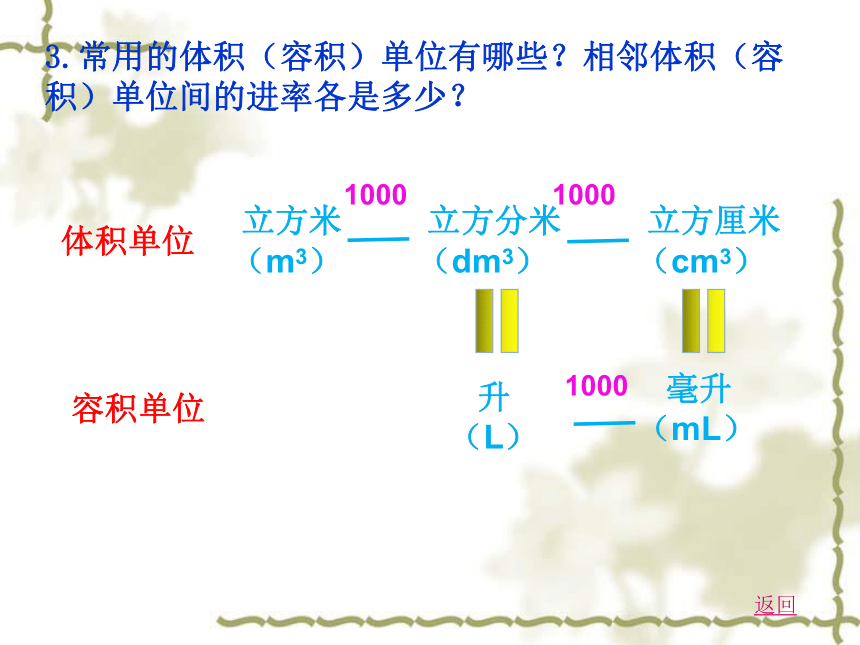
3.常用的体积(容积)单位有哪些?相邻体积(容积)单位间的进率各是多少?
体积单位
立方米
(m3)
立方分米
(dm3)
立方厘米
(cm3)
1000
1000
容积单位
升
(L)
毫升
(mL)
1000
返回
长方体
正方体
圆柱
圆锥
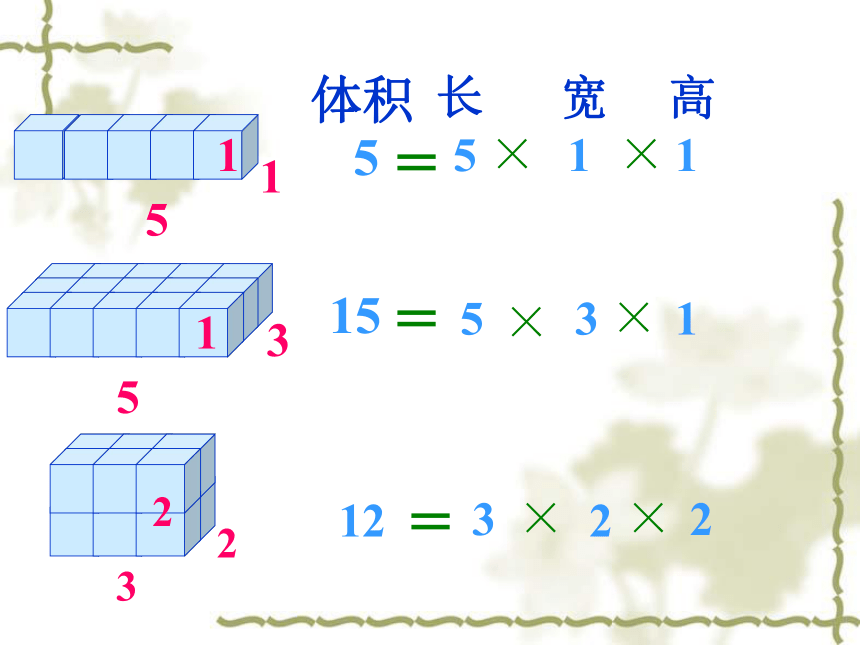
5
体积
长
1
1
宽
1
1
高
15
5
5
3
3
1
1
12
3
3
2
2
2
2
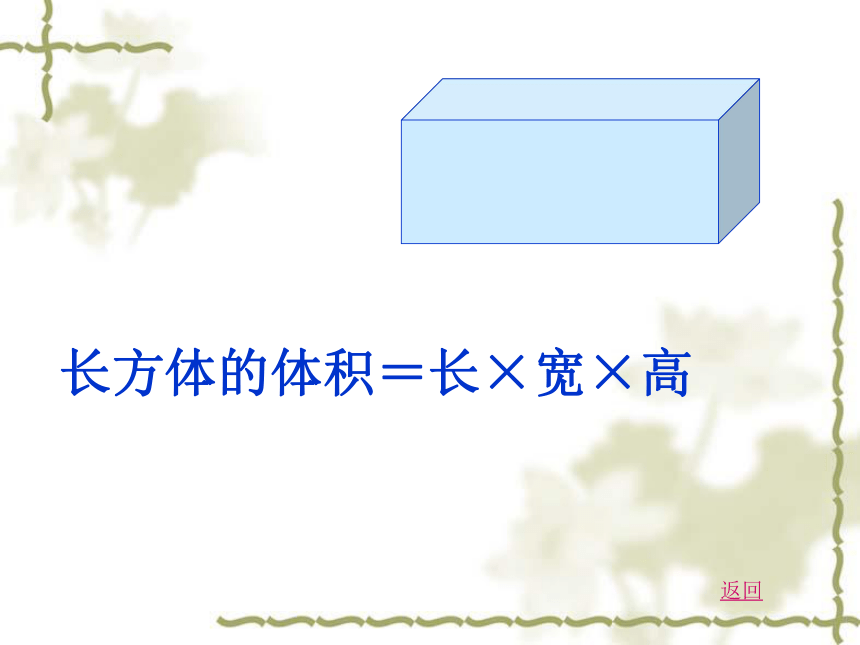
长方体的体积=长×宽×高
返回
棱长
棱长
棱长
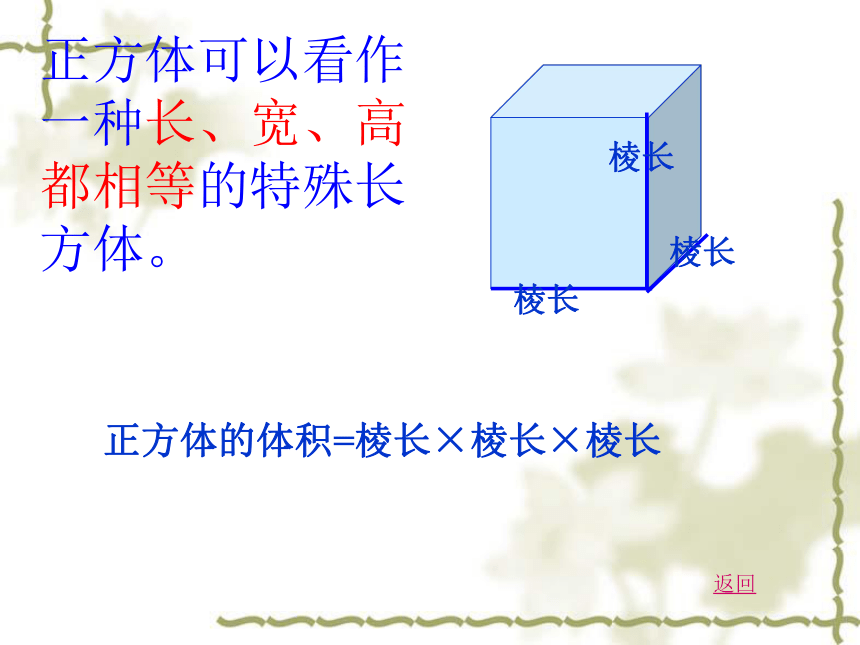
正方体的体积=棱长×棱长×棱长
正方体可以看作一种长、宽、高都相等的特殊长方体。
返回
返回
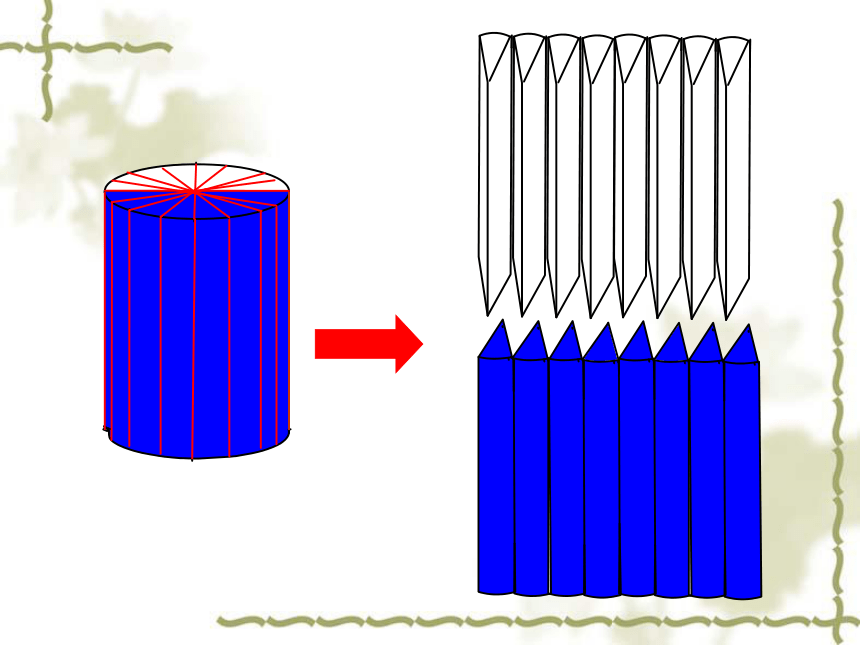
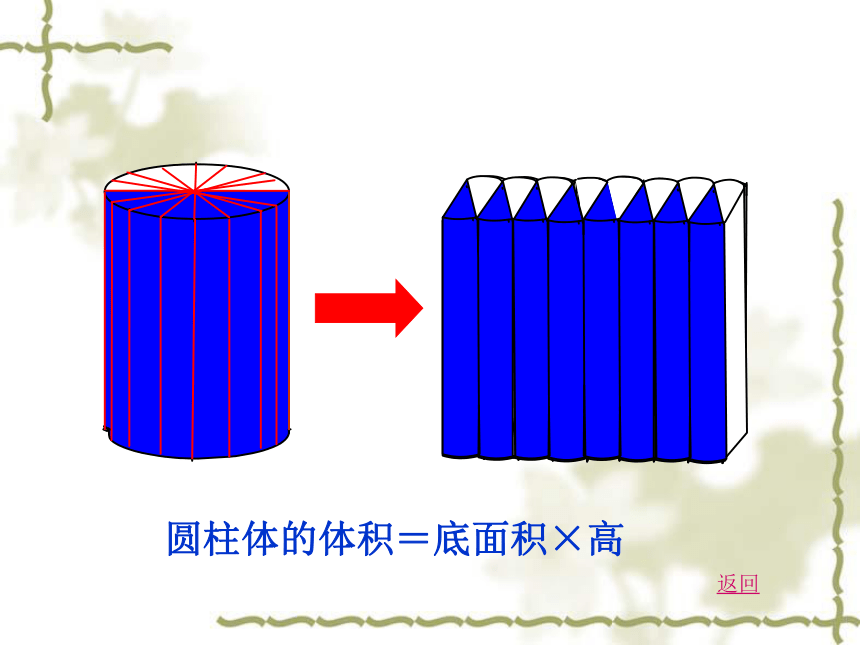
圆柱体的体积=底面积×高
圆锥的高
圆柱的高
底面
等底等高
第1次
第1次
第1次
第1次
第1次
第1次
第1次
第1次
第1次
第2次
第2次
第2次
第2次
第2次
第2次
第2次
第2次
第2次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
1次
1次
2次
2次
3次
3次
圆锥体的体积=底面积×高×
立体图形的表面积和体积有什么区别?
(1)表示的意义不同;
(2)计量的单位不同;
(3)计算的方法不同。
平方米
毫升
立方米
立方分米
升
500
90
1040
4.05
0.06
75
达标检测:
1.完成课本第94页第1-2题。
达标检测
2.仔细辨析,正确判断:
(1)一个圆柱形水桶的体积就是它的容积。(
)
(2)棱长6厘米的正方体,表面积和体积相等。(
)
(3)圆锥的体积等于圆柱体积的
,它们不一定等底等高。(
)
(4)将一个圆柱的底面等分成16份,剪拼成一个近似的长方体,表面积和体积都没改变。(
)
×
×
√
×
联系实际,学有所用(只列式不计算)
一个无盖圆柱形水桶,底面半径是3分米,高是
8分米。
(1)沿水桶上口边沿有一道铁丝箍,铁丝箍长多少分米?
(2)这个水桶的占地面积有多大?
(3)制作这个水桶至少需要铁皮多少平方分米?
(4)这个水桶能盛水多少升?(壁厚忽略不计)
2×π×3
求底面周长
求底面积
π×32
求侧面积和一个底面积的和
2×π×3×8+π×32
求容积
π×32×8
综合应用,提升思维(必做)
1.右图中马铃薯的体积是多少?
2.一个棱长为6厘米的正方体铁块,熔铸成半径为5厘米的
圆锥形铁块,求圆锥的高。(用方程解,要求只列方程)
3.以右面这个直角三角形的一条直角边为轴
旋转一周,得到的形体的体积最大是多少?
π×(10÷2)2×(25-15)
π×32×4×
=12π(cm3)
π×42×3×
=16π(cm3)
16πcm3>12πcm3
综合应用,提升思维(必做)
(4)一个长方体花坛,从里面量长10m,宽2m,高0.8m,四周用砖砌成,砖墙的厚度是0.2米,中间填满泥土。
(1)花坛所占的空间有多大?
(2)花坛里大约有泥土多少立方米?
(3)需要多少立方米的砖?
(10+0.2×2)×(2+0.2×2)×0.8
10×2×0.8
(10+0.2×2)×(2+0.2×2)×0.8-10×2×0.8
勇攀高峰(选做)
从一个棱长6厘米的正方体中挖去一个棱长1厘米的小正方体,剩下的图形和原图形相比,表面积有没有变化?体积呢?如果发生了变化,想一想,发生了怎样的变化?
表面积不变
体积减少1cm3
表面积增加2cm2
体积减少1cm3
表面积增加4cm2
体积减少1cm3
学习目标:
1.我要进一步理解立体图形的表面积和体积(容积)的意义;
2.我要进一步掌握常用的体积(容积)单位及其进率,会进行它们之间的简单换算;
3.我要进一步掌握立体图形表面积和体积的计算方法,并能解决相关的实际问题。
学习目标:
1.我要进一步理解立体图形的表面积和体积(容积)的意义;
2.我要进一步掌握常用的体积(容积)单位及其进率,会进行它们之间的简单换算;
3.我要进一步掌握立体图形表面积和体积的计算方法,并能解决相关的实际问题。
导学单:
小组整理讨论:
1.什么是长方体、正方体和圆柱的表面积?各怎样计算?
2.什么是物体的体积?什么是容器的容积?
3.常用的体积(容积)单位有哪些?相邻体积(容积)单位间的进率各是多少?
4.怎样计算长方体、正方体、圆柱和圆锥的体积?它们的计算公式各是怎样推导出来的,推导时几者之间有什么联系?
1.什么是长方体、正方体和圆柱的表面积?各怎样计算?
围成立体图形的所有面的面积总和,叫作立体图形的表面积。
返回
2.什么是物体的体积?什么是容器的容积?
物体所占空间的大小叫作物体的体积。
容器所能容纳物体的体积叫作容器的容积。
返回
3.常用的体积(容积)单位有哪些?相邻体积(容积)单位间的进率各是多少?
体积单位
立方米
(m3)
立方分米
(dm3)
立方厘米
(cm3)
1000
1000
容积单位
升
(L)
毫升
(mL)
1000
返回
长方体
正方体
圆柱
圆锥
5
体积
长
1
1
宽
1
1
高
15
5
5
3
3
1
1
12
3
3
2
2
2
2
长方体的体积=长×宽×高
返回
棱长
棱长
棱长
正方体的体积=棱长×棱长×棱长
正方体可以看作一种长、宽、高都相等的特殊长方体。
返回
返回
圆柱体的体积=底面积×高
圆锥的高
圆柱的高
底面
等底等高
第1次
第1次
第1次
第1次
第1次
第1次
第1次
第1次
第1次
第2次
第2次
第2次
第2次
第2次
第2次
第2次
第2次
第2次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
第3次
1次
1次
2次
2次
3次
3次
圆锥体的体积=底面积×高×
立体图形的表面积和体积有什么区别?
(1)表示的意义不同;
(2)计量的单位不同;
(3)计算的方法不同。
平方米
毫升
立方米
立方分米
升
500
90
1040
4.05
0.06
75
达标检测:
1.完成课本第94页第1-2题。
达标检测
2.仔细辨析,正确判断:
(1)一个圆柱形水桶的体积就是它的容积。(
)
(2)棱长6厘米的正方体,表面积和体积相等。(
)
(3)圆锥的体积等于圆柱体积的
,它们不一定等底等高。(
)
(4)将一个圆柱的底面等分成16份,剪拼成一个近似的长方体,表面积和体积都没改变。(
)
×
×
√
×
联系实际,学有所用(只列式不计算)
一个无盖圆柱形水桶,底面半径是3分米,高是
8分米。
(1)沿水桶上口边沿有一道铁丝箍,铁丝箍长多少分米?
(2)这个水桶的占地面积有多大?
(3)制作这个水桶至少需要铁皮多少平方分米?
(4)这个水桶能盛水多少升?(壁厚忽略不计)
2×π×3
求底面周长
求底面积
π×32
求侧面积和一个底面积的和
2×π×3×8+π×32
求容积
π×32×8
综合应用,提升思维(必做)
1.右图中马铃薯的体积是多少?
2.一个棱长为6厘米的正方体铁块,熔铸成半径为5厘米的
圆锥形铁块,求圆锥的高。(用方程解,要求只列方程)
3.以右面这个直角三角形的一条直角边为轴
旋转一周,得到的形体的体积最大是多少?
π×(10÷2)2×(25-15)
π×32×4×
=12π(cm3)
π×42×3×
=16π(cm3)
16πcm3>12πcm3
综合应用,提升思维(必做)
(4)一个长方体花坛,从里面量长10m,宽2m,高0.8m,四周用砖砌成,砖墙的厚度是0.2米,中间填满泥土。
(1)花坛所占的空间有多大?
(2)花坛里大约有泥土多少立方米?
(3)需要多少立方米的砖?
(10+0.2×2)×(2+0.2×2)×0.8
10×2×0.8
(10+0.2×2)×(2+0.2×2)×0.8-10×2×0.8
勇攀高峰(选做)
从一个棱长6厘米的正方体中挖去一个棱长1厘米的小正方体,剩下的图形和原图形相比,表面积有没有变化?体积呢?如果发生了变化,想一想,发生了怎样的变化?
表面积不变
体积减少1cm3
表面积增加2cm2
体积减少1cm3
表面积增加4cm2
体积减少1cm3
学习目标:
1.我要进一步理解立体图形的表面积和体积(容积)的意义;
2.我要进一步掌握常用的体积(容积)单位及其进率,会进行它们之间的简单换算;
3.我要进一步掌握立体图形表面积和体积的计算方法,并能解决相关的实际问题。
