人教版九年级数学上册21.3实际问题与一元二次方程(1)课件(16张PPT)
文档属性
| 名称 | 人教版九年级数学上册21.3实际问题与一元二次方程(1)课件(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 160.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 19:41:30 | ||
图片预览




文档简介
(共16张PPT)
21.3
第1课时
实际问题与一元二次方程
知识回顾
1.解一元二次方程有哪些方法?
直接开平方法、配方法、公式法、因式分解法.
2.列一元二次方程解应用题的步骤?
①审题,
②设出未知数,
③找等量关系,
④列方程,
⑤解方程,
⑥验根,
⑦答.
学习目标
1.会分析实际问题中的数量关系并会列一元二次方程.
2.正确分析问题中的数量关系.
3.会找出实际问题中的相等关系并建模解决问题.
课堂导入
同一元一次方程、二元一次方程(组)等一样,一元二次方程也可以作为反映某些实际问题中数量关系的数学模型.本节讨论如何利用一元二次方程解决实际问题.
知识点
新知探究
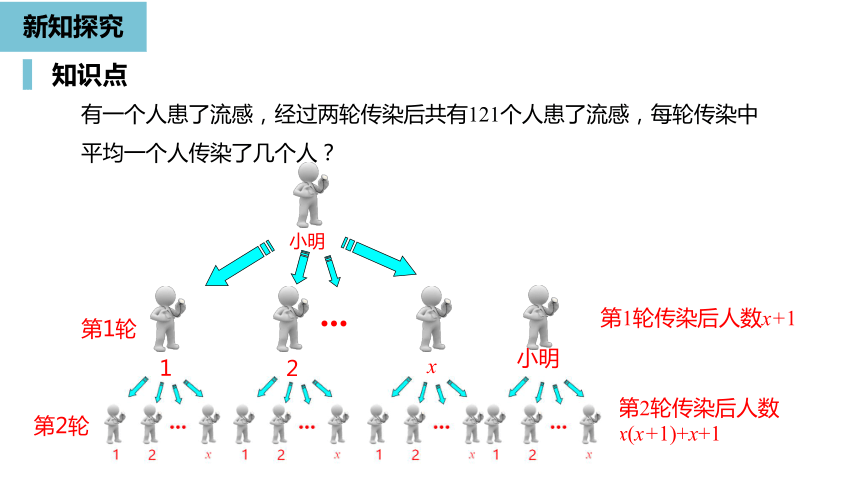
有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
小明
第1轮
第1轮传染后人数x+1
第2轮传染后人数
x(x+1)+x+1
小明
1
2
x
???
第2轮
知识点
新知探究
x1=
,
x2=
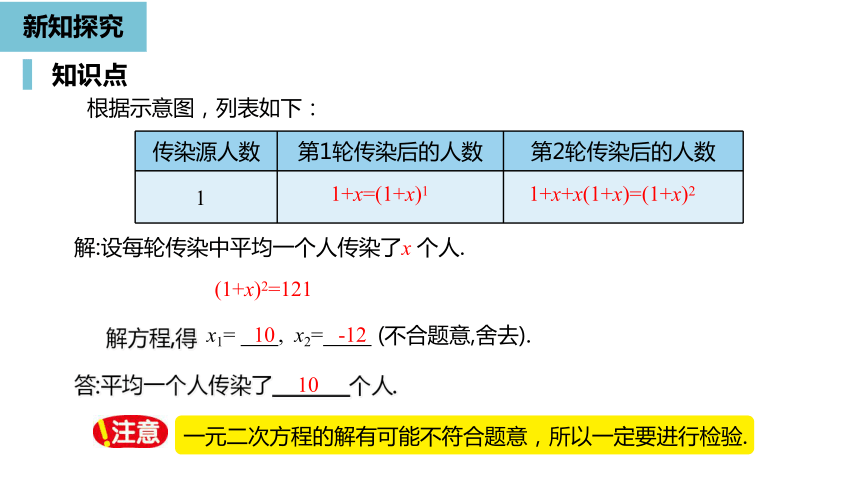
根据示意图,列表如下:
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去).
10
解:设每轮传染中平均一个人传染了x
个人.
(1+x)2=121
传染源人数
第1轮传染后的人数
第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
一元二次方程的解有可能不符合题意,所以一定要进行检验.
知识点
新知探究
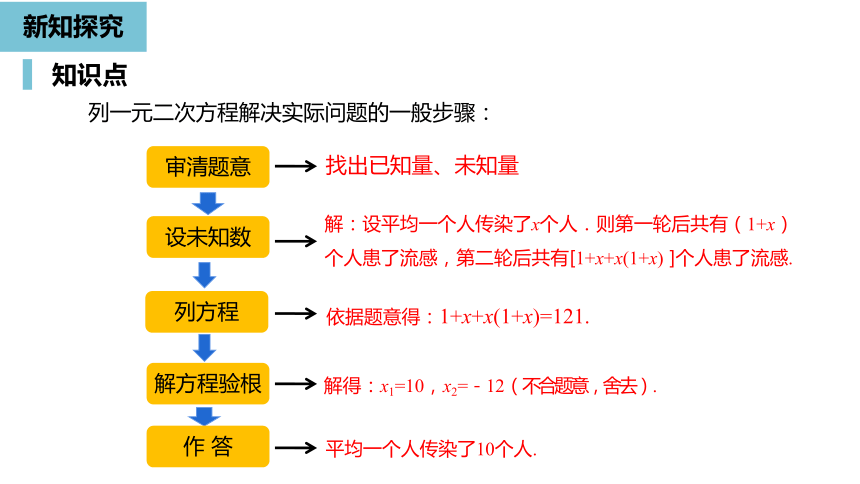
审清题意
设未知数
列方程
解方程验根
作
答
找出已知量、未知量
解:设平均一个人传染了x个人.则第一轮后共有(1+x)个人患了流感,第二轮后共有[1+x+x(1+x)
]个人患了流感.
依据题意得:1+x+x(1+x)=121.
解得:x1=10,x2=-12(不合题意,舍去).
平均一个人传染了10个人.
列一元二次方程解决实际问题的一般步骤:
知识点
新知探究
如果按照这样的传染速度,三轮传染后有多少人患流感?
第2种做法
以第2轮传染后的人数121为传染源,传染一次后就是:
121(1+x)=121(1+10)=1
331.
第一轮传染后的人数
第二轮传染后的人数
第三轮传染后的人数
(1+x)1
(1+x)2
第1种做法
以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1
331.
(1+x)3
知识点
新知探究
传染源
新增患者人数
本轮结束患者总人数
第一轮
1
1?x=x
1+x
第二轮
1+x
(1+x)x
1+x+(1+x)x=
第三轮
第
n
轮
如果按这样的传染速度,n
轮传染后有多少人患了流感?
(1+x)2
(1+x)n
(1+x)3
经过n轮传染后共有
(1+x)n
人患流感.
(1+x)2
(1+x)2?x
(1+x)2+(1+x)2?x=
(1+x)n-1
(1+x)n-1?x
跟踪训练
新知探究
有一株月季,它的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数是
73,设每个支干长出
x
个小分支,根据题意可列方程为(
)
B
A.1+x+x(1+x)=73
B.1+x+x2=73
C.1+x2
=73
D.(1+x)2=73
随堂练习
1
两个相邻偶数的积是168.求这两个偶数的和.
解:设较小的偶数为
x,则另一个偶数为
(x+2),
依题意,得
x(x+2)=168,解得
x1=12,x2=-14,
∴x+2=14或
x+2=-12,
∴x+(x+2)=±26.
答:这两个偶数的和为±26.
随堂练习
2
早期,甲肝流行,传染性很强,曾有
2
人同时患上甲肝.在一天内,一人平均能传染
x
人,经过两天传染后
128
人患上甲肝,则
x
的值为(
)
A.10
B.9
C.8
D.7
D
解:依题意得
2+2x+x(2+2x)=128,
解得
x1=7,x2=-9(不合题意,舍去).
故
x
的值为7.
课堂小结
建立一元二次方程方程
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检
验
运用一元二次方程方程解决实际问题的步骤有哪些?
答
对接中考
1
电脑病毒感染的传播非常快,如果开始有
6
台电脑被感染,经过两轮感染后共有
2
400
台电脑被感染.
每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染
x
台电脑.
答:每轮感染中平均一台电脑会感染19台电脑.
解得x1=19
或
x2=
-21
(舍去)
依题意得
6+6x+6x
(1+x)
=2
400
6
(1+x)2
=2
400
对接中考
2
某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是
91,每个支干长出多少小分支?
解:设每个支干长出
x
个小分支,
则1+x+x2=91,
即x2+x?90=0,
解得x1=9,x2=-10(不合题意,舍去)
答:每个支干长出
9
个小分支.
对接中考
3
甲型流感病毒的传染性极强,某地因
1
人患了甲型流感没有及时隔离治疗,经过两天的传染后共有
9
人患了甲型流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过
5
天的传染后,这个地区一共将会有多少人患甲型流感?
解:设每天平均一个人传染了
x
人,
解得
x1=-4
(舍去),x2=2.
答:每天平均一个人传染了
2
人,这个地区一共将会有
2
187
人患甲型流感.
1+x+x(1+x)=9,
即(1+x)2=9.
9(1+x)5=9(1+2)5=2
187
或
(1+x)7=
(1+2)7=2
187.
21.3
第1课时
实际问题与一元二次方程
知识回顾
1.解一元二次方程有哪些方法?
直接开平方法、配方法、公式法、因式分解法.
2.列一元二次方程解应用题的步骤?
①审题,
②设出未知数,
③找等量关系,
④列方程,
⑤解方程,
⑥验根,
⑦答.
学习目标
1.会分析实际问题中的数量关系并会列一元二次方程.
2.正确分析问题中的数量关系.
3.会找出实际问题中的相等关系并建模解决问题.
课堂导入
同一元一次方程、二元一次方程(组)等一样,一元二次方程也可以作为反映某些实际问题中数量关系的数学模型.本节讨论如何利用一元二次方程解决实际问题.
知识点
新知探究
有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
小明
第1轮
第1轮传染后人数x+1
第2轮传染后人数
x(x+1)+x+1
小明
1
2
x
???
第2轮
知识点
新知探究
x1=
,
x2=
根据示意图,列表如下:
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去).
10
解:设每轮传染中平均一个人传染了x
个人.
(1+x)2=121
传染源人数
第1轮传染后的人数
第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
一元二次方程的解有可能不符合题意,所以一定要进行检验.
知识点
新知探究
审清题意
设未知数
列方程
解方程验根
作
答
找出已知量、未知量
解:设平均一个人传染了x个人.则第一轮后共有(1+x)个人患了流感,第二轮后共有[1+x+x(1+x)
]个人患了流感.
依据题意得:1+x+x(1+x)=121.
解得:x1=10,x2=-12(不合题意,舍去).
平均一个人传染了10个人.
列一元二次方程解决实际问题的一般步骤:
知识点
新知探究
如果按照这样的传染速度,三轮传染后有多少人患流感?
第2种做法
以第2轮传染后的人数121为传染源,传染一次后就是:
121(1+x)=121(1+10)=1
331.
第一轮传染后的人数
第二轮传染后的人数
第三轮传染后的人数
(1+x)1
(1+x)2
第1种做法
以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1
331.
(1+x)3
知识点
新知探究
传染源
新增患者人数
本轮结束患者总人数
第一轮
1
1?x=x
1+x
第二轮
1+x
(1+x)x
1+x+(1+x)x=
第三轮
第
n
轮
如果按这样的传染速度,n
轮传染后有多少人患了流感?
(1+x)2
(1+x)n
(1+x)3
经过n轮传染后共有
(1+x)n
人患流感.
(1+x)2
(1+x)2?x
(1+x)2+(1+x)2?x=
(1+x)n-1
(1+x)n-1?x
跟踪训练
新知探究
有一株月季,它的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数是
73,设每个支干长出
x
个小分支,根据题意可列方程为(
)
B
A.1+x+x(1+x)=73
B.1+x+x2=73
C.1+x2
=73
D.(1+x)2=73
随堂练习
1
两个相邻偶数的积是168.求这两个偶数的和.
解:设较小的偶数为
x,则另一个偶数为
(x+2),
依题意,得
x(x+2)=168,解得
x1=12,x2=-14,
∴x+2=14或
x+2=-12,
∴x+(x+2)=±26.
答:这两个偶数的和为±26.
随堂练习
2
早期,甲肝流行,传染性很强,曾有
2
人同时患上甲肝.在一天内,一人平均能传染
x
人,经过两天传染后
128
人患上甲肝,则
x
的值为(
)
A.10
B.9
C.8
D.7
D
解:依题意得
2+2x+x(2+2x)=128,
解得
x1=7,x2=-9(不合题意,舍去).
故
x
的值为7.
课堂小结
建立一元二次方程方程
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检
验
运用一元二次方程方程解决实际问题的步骤有哪些?
答
对接中考
1
电脑病毒感染的传播非常快,如果开始有
6
台电脑被感染,经过两轮感染后共有
2
400
台电脑被感染.
每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染
x
台电脑.
答:每轮感染中平均一台电脑会感染19台电脑.
解得x1=19
或
x2=
-21
(舍去)
依题意得
6+6x+6x
(1+x)
=2
400
6
(1+x)2
=2
400
对接中考
2
某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是
91,每个支干长出多少小分支?
解:设每个支干长出
x
个小分支,
则1+x+x2=91,
即x2+x?90=0,
解得x1=9,x2=-10(不合题意,舍去)
答:每个支干长出
9
个小分支.
对接中考
3
甲型流感病毒的传染性极强,某地因
1
人患了甲型流感没有及时隔离治疗,经过两天的传染后共有
9
人患了甲型流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过
5
天的传染后,这个地区一共将会有多少人患甲型流感?
解:设每天平均一个人传染了
x
人,
解得
x1=-4
(舍去),x2=2.
答:每天平均一个人传染了
2
人,这个地区一共将会有
2
187
人患甲型流感.
1+x+x(1+x)=9,
即(1+x)2=9.
9(1+x)5=9(1+2)5=2
187
或
(1+x)7=
(1+2)7=2
187.
同课章节目录
