人教版九年级数学上册22.3实际问题与二次函数(3)课件(21张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数(3)课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 793.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 19:56:01 | ||
图片预览







文档简介
(共21张PPT)
22.3
第3课时
实际问题与二次函数
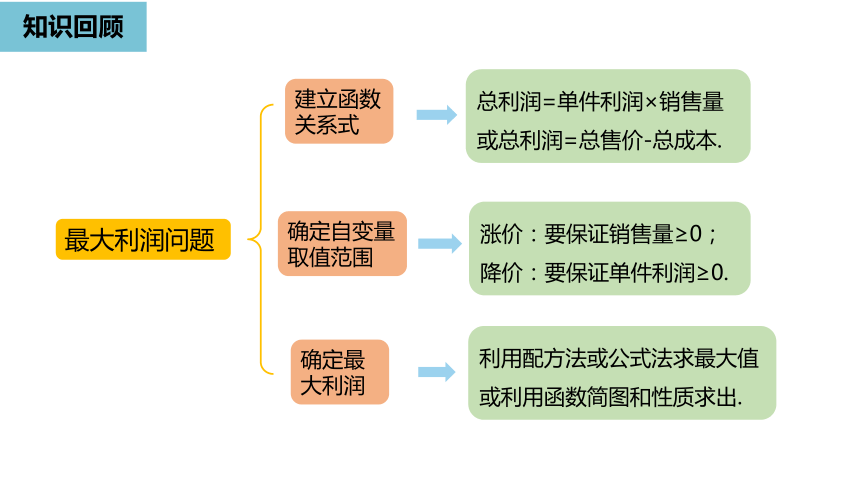
知识回顾
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
利用配方法或公式法求最大值或利用函数简图和性质求出.
学习目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.
2.利用二次函数解决拱桥及运动中的有关问题.
3.能运用二次函数的图象与性质进行决策.
课堂导入
前面我们已经学习了利用二次函数解决几何最值问题及实际问题中的最值问题,本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
知识点1
新知探究
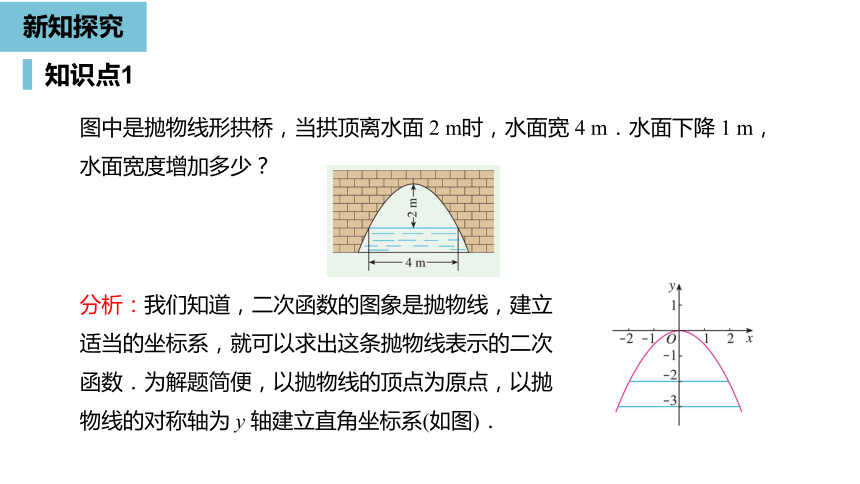
图中是抛物线形拱桥,当拱顶离水面
2
m时,水面宽
4
m.水面下降
1
m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为
y
轴建立直角坐标系(如图).
知识点1
新知探究
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-
这条抛物线表示的二次函数为y=-
x2.
当水面下降1
m时,水面的纵坐标为-3.
当
y
=
-3时,-
x2=
-3,解得
x1=
,x2=
-
,
所以当水面下降1
m时,水面宽度为
m.
水面下降1
m,水面宽度增加________m.
知识点1
新知探究
解决抛物线型建筑问题的步骤:
(1)建立适当的平面直角坐标系,将抛物线形的图形放在坐标系中;
(2)设出函数解析式,结合图形和已知条件,用待定系数法求函数解析式;
(3)利用二次函数的图象与性质求解实际问题.
同一个问题中,建立平面直角坐标系的方法有多种,建立适当的平面直角坐标系能简化函数解析式.通常应使已知点在坐标轴上。
解:
(1)
答案不唯一.如以
AB
所在直线为
x
轴,以
AB
的中点为原点建立平面直角坐标系
xOy,如图所示,
则
A(
-4,0),B(4,0),C(0,6).
设这条抛物线的解析式为
y=a(x-4)(x+4).
将
C(0,6)代入,得
-16a=6,
所以抛物线的解析式为
y
.
跟踪训练
新知探究
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度
AB=8
m,隧道的最高点
C
到公路的距离为
6
m.
(1)建立适当的平面直角坐标系,求抛物线的解析式;
解:(2)
由(1)知抛物线的解析式为
y
.
当
x=1时,y=
.
因为4.4+0.5=4.9<
,
所以这辆货车能安全通过这条隧道.
跟踪训练
新知探究
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度
AB=8
m,隧道的最高点
C
到公路的距离为
6
m.
(2)现有一辆货车的高度是
4.4
m,货车的宽度是
2
m.为了保证安全,车顶距离隧道顶部至少
0.5
m,通过计算说明这辆货车能否安全通过这条隧道.
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在
O
点正上方
1
m
的
P
处发出一球,羽毛球飞行的高度
y(m)
与水平距离
x(m)
之间满足函数解析式
y=a(x-4)2+h,已知点
O
与球网的水平距离为
5
m,球网的高度为
1.55
m.
(1)当a=-时,①求
h
的值;②通过计算判断此球能否过网;
解:(1)
①
当a=时,y=(x-4)2+h,
将点P(0,1)代入,得×16+h=1,
解得h=
.
知识点2
新知探究
解:(1)
②
把x=5代入y=(x-4)2+,
得y=×(5-4)2+=1.625,
∵1.625>1.55,∴此球能过网.
知识点2
新知探究
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在
O
点正上方
1
m
的
P
处发出一球,羽毛球飞行的高度
y(m)
与水平距离
x(m)
之间满足函数解析式
y=a(x-4)2+h,已知点
O
与球网的水平距离为
5
m,球网的高度为
1.55
m.
(1)当a=-时,①求
h
的值;②通过计算判断此球能否过网;
解:(2)
把(0,1),(7,)代入y=a(x-4)2+h,
得
解得∴a=.
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在
O
点正上方
1
m
的
P
处发出一球,羽毛球飞行的高度
y(m)
与水平距离
x(m)
之间满足函数解析式
y=a(x-4)2+h,已知点
O
与球网的水平距离为
5
m,球网的高度为
1.55
m.
(2)若甲发球过网后,羽毛球飞行到与点
O
的水平距离为
7
m,离地面的高度为
m
的
Q
处时,乙扣球成功,求
a
的值.
知识点2
新知探究
解决抛物线型运动路线问题时:一定要分析清楚抛物线的横、纵坐标的实际意义,再利用二次函数的图象和性质解题.
知识点2
新知探究
随堂练习
1
解:(1)
建立如图所示的平面直角坐标系,
设所求抛物线的解析式为
y=ax2,点D的坐标为
D(5,b),则B(10,b-3),
把D、B的坐标分别代入y=ax2得解得
∴抛物线的解析式为y=
-
x2.
如图,某河面上有一座抛物线形拱桥,桥下水面在正常水位
AB时,宽为
20
m,若水位上升
3
m,水面就会达到警戒线
CD,这时水面宽度为
10
m.
(1)
建立适当的平面直角坐标系并求出抛物线的解析式;
随堂练习
1
如图,某河面上有一座抛物线形拱桥,桥下水面在正常水位
AB时,宽为
20
m,若水位上升
3
m,水面就会达到警戒线
CD,这时水面宽度为
10
m.
(2)
若洪水到来时,水位以每小时
0.2
m
的速度上升,从警戒线开始,再持续多少小时就能到达拱桥的拱顶?
解:(2)
∵b=
-1,
∴拱桥顶O到CD的距离为1m,
=5(h),所以再持续5小时到达拱桥的拱顶.
随堂练习
2
(2018?武汉中考)飞机着陆后滑行的距离
y(单位:m)关于滑行时间
t(单位:s)的函数解析式是
y=60t-t2.在飞机着陆滑行中,最后
4
s滑行的距离是
m.
24
解:当y取得最大值时,飞机停下来,
则y=60t-1.5t2=-1.5(t-20)2+600,
当t=20时,y取得最大值,即飞机着陆后滑行20
s时,滑行距离为600米.
因此
t
的取值范围是0≤t≤20;
当t=16时,y=576,
所以最后
4
s滑行的距离是600-576=24(米).
课堂小结
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线型问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
对接中考
1
发射一枚炮弹,经过
x
秒后炮弹的高度为
y
米,x,y
满足
y=ax2+bx,其中
a,b
是常数,且
a≠0.若此炮弹在第
6
秒与第
14
秒时的高度相等,则炮弹达到最大高度的时刻是(
)
B
A.第8秒
B.第10秒
C.第12秒
D.第15秒
解:∵x取6和14时y的值相等,
∴抛物线y=ax2+bx的对称轴为直线x=6+=10,
即炮弹达到最大高度的时刻是第10
秒.
对接中考
2
拱桥呈抛物线形,其函数解析式为
y=
-
x2,当拱桥下水面宽为
12
m
时,水面离拱桥顶端的高度是(
)
D
A.3
m
B.2
m
C.4
m
D.9
m
解:由题意可得x=6时,y=-×62=-9.
故水面离拱桥顶端的高度是9
m.
对接中考
3
一位篮球运动员在距离篮圈中心水平距离
4
m
处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为
2.5
m
时,达到最大高度
3.5
m,然后准确落入篮框内,已知篮圈中心距离地面高度为
3.05
m,在如图所示的平面直角坐标系中,下列说法正确的是
(
)
A
A.此抛物线的解析式是
y=-x2
+3.5
B.篮圈中心的坐标是
(4,3.05)
C.此抛物线的顶点坐标是
(3.5,0)
D.篮球出手时离地面的高度是
2
m
对接中考
3
解:选项A中,∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数解析式为y=ax2+3.5,
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入得??3.05=a×1.52+3.5,∴a=-0.2,∴y=-0.2x2+3.5,故本选项正确;
选项B中,由图示知,篮圈中心的坐标是(1.5,3.05),故本选项错误;
选项C中,由图示知,此抛物线的顶点坐标是(0,3.5),故本选项错误;
选项D中,设这次跳投时,球出手处离地面h
m,
∵由选项A可知y=-0.2x2+3.5,∴当x=-2.5时,h=-0.2×(-2.5)2+3.5=2.25.
∴这次跳投时,球出手处离地面2.25
m.故本选项错误.
22.3
第3课时
实际问题与二次函数
知识回顾
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
利用配方法或公式法求最大值或利用函数简图和性质求出.
学习目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.
2.利用二次函数解决拱桥及运动中的有关问题.
3.能运用二次函数的图象与性质进行决策.
课堂导入
前面我们已经学习了利用二次函数解决几何最值问题及实际问题中的最值问题,本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
知识点1
新知探究
图中是抛物线形拱桥,当拱顶离水面
2
m时,水面宽
4
m.水面下降
1
m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为
y
轴建立直角坐标系(如图).
知识点1
新知探究
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-
这条抛物线表示的二次函数为y=-
x2.
当水面下降1
m时,水面的纵坐标为-3.
当
y
=
-3时,-
x2=
-3,解得
x1=
,x2=
-
,
所以当水面下降1
m时,水面宽度为
m.
水面下降1
m,水面宽度增加________m.
知识点1
新知探究
解决抛物线型建筑问题的步骤:
(1)建立适当的平面直角坐标系,将抛物线形的图形放在坐标系中;
(2)设出函数解析式,结合图形和已知条件,用待定系数法求函数解析式;
(3)利用二次函数的图象与性质求解实际问题.
同一个问题中,建立平面直角坐标系的方法有多种,建立适当的平面直角坐标系能简化函数解析式.通常应使已知点在坐标轴上。
解:
(1)
答案不唯一.如以
AB
所在直线为
x
轴,以
AB
的中点为原点建立平面直角坐标系
xOy,如图所示,
则
A(
-4,0),B(4,0),C(0,6).
设这条抛物线的解析式为
y=a(x-4)(x+4).
将
C(0,6)代入,得
-16a=6,
所以抛物线的解析式为
y
.
跟踪训练
新知探究
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度
AB=8
m,隧道的最高点
C
到公路的距离为
6
m.
(1)建立适当的平面直角坐标系,求抛物线的解析式;
解:(2)
由(1)知抛物线的解析式为
y
.
当
x=1时,y=
.
因为4.4+0.5=4.9<
,
所以这辆货车能安全通过这条隧道.
跟踪训练
新知探究
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度
AB=8
m,隧道的最高点
C
到公路的距离为
6
m.
(2)现有一辆货车的高度是
4.4
m,货车的宽度是
2
m.为了保证安全,车顶距离隧道顶部至少
0.5
m,通过计算说明这辆货车能否安全通过这条隧道.
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在
O
点正上方
1
m
的
P
处发出一球,羽毛球飞行的高度
y(m)
与水平距离
x(m)
之间满足函数解析式
y=a(x-4)2+h,已知点
O
与球网的水平距离为
5
m,球网的高度为
1.55
m.
(1)当a=-时,①求
h
的值;②通过计算判断此球能否过网;
解:(1)
①
当a=时,y=(x-4)2+h,
将点P(0,1)代入,得×16+h=1,
解得h=
.
知识点2
新知探究
解:(1)
②
把x=5代入y=(x-4)2+,
得y=×(5-4)2+=1.625,
∵1.625>1.55,∴此球能过网.
知识点2
新知探究
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在
O
点正上方
1
m
的
P
处发出一球,羽毛球飞行的高度
y(m)
与水平距离
x(m)
之间满足函数解析式
y=a(x-4)2+h,已知点
O
与球网的水平距离为
5
m,球网的高度为
1.55
m.
(1)当a=-时,①求
h
的值;②通过计算判断此球能否过网;
解:(2)
把(0,1),(7,)代入y=a(x-4)2+h,
得
解得∴a=.
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在
O
点正上方
1
m
的
P
处发出一球,羽毛球飞行的高度
y(m)
与水平距离
x(m)
之间满足函数解析式
y=a(x-4)2+h,已知点
O
与球网的水平距离为
5
m,球网的高度为
1.55
m.
(2)若甲发球过网后,羽毛球飞行到与点
O
的水平距离为
7
m,离地面的高度为
m
的
Q
处时,乙扣球成功,求
a
的值.
知识点2
新知探究
解决抛物线型运动路线问题时:一定要分析清楚抛物线的横、纵坐标的实际意义,再利用二次函数的图象和性质解题.
知识点2
新知探究
随堂练习
1
解:(1)
建立如图所示的平面直角坐标系,
设所求抛物线的解析式为
y=ax2,点D的坐标为
D(5,b),则B(10,b-3),
把D、B的坐标分别代入y=ax2得解得
∴抛物线的解析式为y=
-
x2.
如图,某河面上有一座抛物线形拱桥,桥下水面在正常水位
AB时,宽为
20
m,若水位上升
3
m,水面就会达到警戒线
CD,这时水面宽度为
10
m.
(1)
建立适当的平面直角坐标系并求出抛物线的解析式;
随堂练习
1
如图,某河面上有一座抛物线形拱桥,桥下水面在正常水位
AB时,宽为
20
m,若水位上升
3
m,水面就会达到警戒线
CD,这时水面宽度为
10
m.
(2)
若洪水到来时,水位以每小时
0.2
m
的速度上升,从警戒线开始,再持续多少小时就能到达拱桥的拱顶?
解:(2)
∵b=
-1,
∴拱桥顶O到CD的距离为1m,
=5(h),所以再持续5小时到达拱桥的拱顶.
随堂练习
2
(2018?武汉中考)飞机着陆后滑行的距离
y(单位:m)关于滑行时间
t(单位:s)的函数解析式是
y=60t-t2.在飞机着陆滑行中,最后
4
s滑行的距离是
m.
24
解:当y取得最大值时,飞机停下来,
则y=60t-1.5t2=-1.5(t-20)2+600,
当t=20时,y取得最大值,即飞机着陆后滑行20
s时,滑行距离为600米.
因此
t
的取值范围是0≤t≤20;
当t=16时,y=576,
所以最后
4
s滑行的距离是600-576=24(米).
课堂小结
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线型问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
对接中考
1
发射一枚炮弹,经过
x
秒后炮弹的高度为
y
米,x,y
满足
y=ax2+bx,其中
a,b
是常数,且
a≠0.若此炮弹在第
6
秒与第
14
秒时的高度相等,则炮弹达到最大高度的时刻是(
)
B
A.第8秒
B.第10秒
C.第12秒
D.第15秒
解:∵x取6和14时y的值相等,
∴抛物线y=ax2+bx的对称轴为直线x=6+=10,
即炮弹达到最大高度的时刻是第10
秒.
对接中考
2
拱桥呈抛物线形,其函数解析式为
y=
-
x2,当拱桥下水面宽为
12
m
时,水面离拱桥顶端的高度是(
)
D
A.3
m
B.2
m
C.4
m
D.9
m
解:由题意可得x=6时,y=-×62=-9.
故水面离拱桥顶端的高度是9
m.
对接中考
3
一位篮球运动员在距离篮圈中心水平距离
4
m
处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为
2.5
m
时,达到最大高度
3.5
m,然后准确落入篮框内,已知篮圈中心距离地面高度为
3.05
m,在如图所示的平面直角坐标系中,下列说法正确的是
(
)
A
A.此抛物线的解析式是
y=-x2
+3.5
B.篮圈中心的坐标是
(4,3.05)
C.此抛物线的顶点坐标是
(3.5,0)
D.篮球出手时离地面的高度是
2
m
对接中考
3
解:选项A中,∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数解析式为y=ax2+3.5,
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入得??3.05=a×1.52+3.5,∴a=-0.2,∴y=-0.2x2+3.5,故本选项正确;
选项B中,由图示知,篮圈中心的坐标是(1.5,3.05),故本选项错误;
选项C中,由图示知,此抛物线的顶点坐标是(0,3.5),故本选项错误;
选项D中,设这次跳投时,球出手处离地面h
m,
∵由选项A可知y=-0.2x2+3.5,∴当x=-2.5时,h=-0.2×(-2.5)2+3.5=2.25.
∴这次跳投时,球出手处离地面2.25
m.故本选项错误.
同课章节目录
