人教版九年级数学上册23.1图形的旋转(1)课件(23张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.1图形的旋转(1)课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 671.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 19:58:34 | ||
图片预览






文档简介
(共23张PPT)
23.1
第1课时
图形的旋转
知识回顾
同学们都见过风车吧,它能在风的吹动下不停地转动.在我们周围,还能看到许多转动着的物体,如车轮、水车、风力发电机、飞机的螺旋桨、时钟的指针、游乐园的大转盘……我们就生活在一个处处能见到旋转现象的世界中.
学习目标
1.掌握旋转的有关概念及基本性质.
2.能够根据旋转的基本性质解决实际问题.
课堂导入
在数学中,旋转是图形变化的方法之一,应该怎样描述它呢?它又有什么性质呢?本章将解答这些问题.
让我们一起来探索旋转的奥秘吧!
知识点1
新知探究
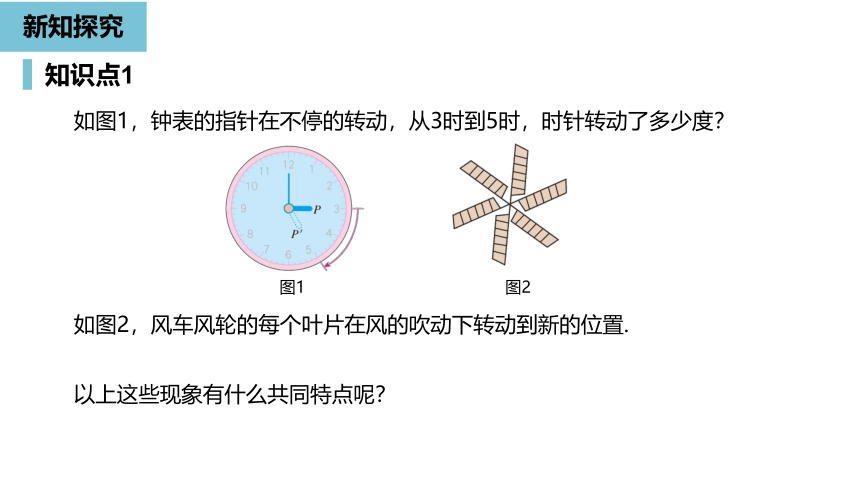
如图1,钟表的指针在不停的转动,从3时到5时,时针转动了多少度?
如图2,风车风轮的每个叶片在风的吹动下转动到新的位置.
图1
图2
以上这些现象有什么共同特点呢?
知识点1
新知探究
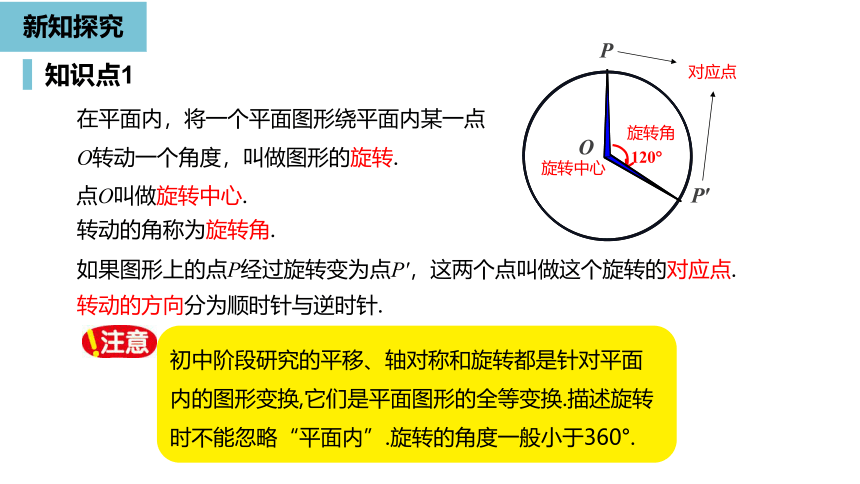
在平面内,将一个平面图形绕平面内某一点O转动一个角度,叫做图形的旋转.
O
P′
P
旋转中心
旋转角
对应点
点O叫做旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
初中阶段研究的平移、轴对称和旋转都是针对平面内的图形变换,它们是平面图形的全等变换.描述旋转时不能忽略“平面内”.旋转的角度一般小于360°.
知识点1
新知探究
1.旋转中心在旋转的过程中是静止不动的,旋转中心可以在图形的外部,也可以在图形的内部,还可以在图形上.
2.将一个图形绕一个定点沿某个方向转动一个角度,意味着图形上每一个点同时按相同方向旋转相同的角度.
3.旋转的三要素:旋转中心,旋转角,旋转方向.
知识点1
新知探究
一个图形由一个位置旋转到另一个位置,固定不动的点就是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
跟踪训练
新知探究
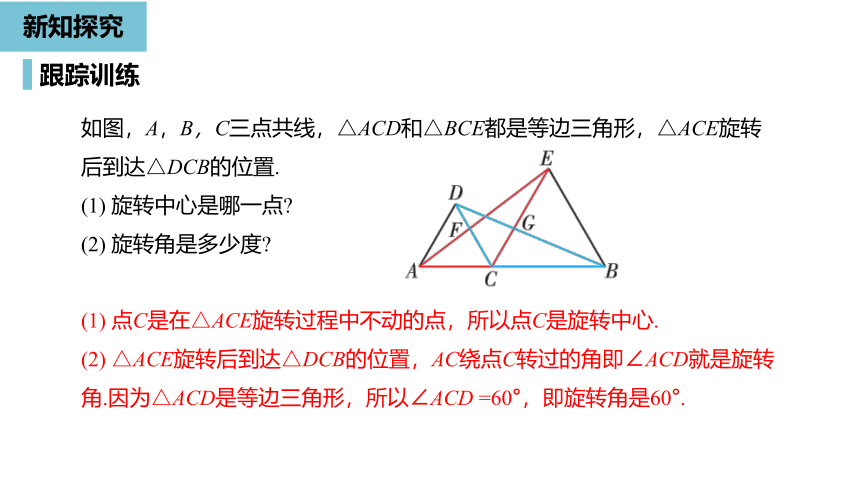
如图,A,B,C三点共线,△ACD和△BCE都是等边三角形,△ACE旋转后到达△DCB的位置.
(1)
旋转中心是哪一点?
(2)
旋转角是多少度?
(1)
点C是在△ACE旋转过程中不动的点,所以点C是旋转中心.
(2)
△ACE旋转后到达△DCB的位置,AC绕点C转过的角即∠ACD就是旋转角.因为△ACD是等边三角形,所以∠ACD
=60°,即旋转角是60°.
知识点2
新知探究
如图,在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△
),移开硬纸板.
△
是由△ABC绕点O旋转得到的.线
段OA与OA′有什么关系?∠AOA′与∠BOB′有什么关系?
△ABC与△
的形状和大小有什么关系?
知识点2
新知探究
A
B
C
B′
C′
O
A
B
C
·
A′
B′
C′
旋转前、后的图形全等,即对应角相等,对应边相等.
对应点到旋转中心的距离相等.
知识点2
新知探究
B'
A'
C'
A
B
C
O
线:
AO=A'O
,BO=B'O
,CO=C'O
角:∠AOA'=∠BOB'
=∠COC'
观察下图,你能得到什么结论?
知识点2
新知探究
(1)
旋转不改变图形的形状和大小,只改变图形的位置;
(2)
旋转时,图形上的每一点都绕旋转中心旋转相同的角度;
(3)
旋转的性质中所说的“对应点”是指“任意一对对应点”,并且对应点到旋转中心的距离相等.
知识点2
新知探究
旋转中心的确定
根据旋转的性质可知,对应点到旋转中心的距离相等,所以旋转中心位于对应点连线的垂直平分线上,即旋转中心是两对对应点所连线段的垂直平分线的交点.
跟踪训练
新知探究
如图,将△ABC
绕点A逆时针旋转得到△ADE,点C
和点E是对应点,若∠CAE=90°,AB=1,则BD=
.
解:将△ABC
绕点
A
逆时针旋转得到△ADE,点
C
和点
E
是对应点,
所以
AB=AD=1,∠BAD=∠CAE=90°,
所以
BD=.
随堂练习
1
如图,在边长为1的正方形网格中,将△ABC绕点P顺时针旋转90°得到△A′B′C′
,则点P的坐标是(
)
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
B
解:∵将△ABC以点P为旋转中心,顺时针旋转90°得到△A′B′C′,
∴点A的对应点为点A′,点C的对应点为点C′,
作线段AA′和CC′的垂直平分线,它们的交点为(1,2),
∴点P的坐标为(1,2).
P
如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°
,则CD的长为(
)
A.0.5
B.1.5
C.
D.1
随堂练习
2
D
解:∵∠BAC=90°,∠B=60°,∴BC=2AB=2,
∵Rt△ABC
绕点
A
按顺时针旋转一定角度得到Rt△ADE,
点
B
的对应点
D
恰好落在
BC
边上,
∴AD=AB,
而∠B=60°,∴△ABD
为等边三角形,
∴BD=AB=1,∴CD=BC-BD=2-1=1.
随堂练习
3
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB'C'
的位置,使得
CC′
//AB,则∠BAB′
的度数是(
)
A.30°
B.35°
C.40°
D.50°
A
解:∵CC′∥AB,∠CAB=75°,
∴∠C′CA=∠CAB=75°,
又∵C,C′
为对应点,点
A
为旋转中心,
∴AC=AC′,即△ACC′
为等腰三角形,
∴∠BAB′=∠CAC′=180°-2∠C′CA=30°.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
对接中考
1
如图,正方形ABCD和正方形EFGO的边长都是1,正方形EFGO绕点O旋转时,两个正方形重叠部分的面积是(
)
A.
B.
C.
D.不能确定
A
解:∵四边形
ABCD
和四边形
EFGO
都是正方形,
∴OB=OC,∠OBC=∠OCB=45°,∠BOC=∠EOG=90°,
∴∠BON=∠COM.
在△OBN
与△OCM
中,
∴△OBN≌△OCM(ASA),∴S△OBN=S△OCM,
∴S四边形OMBN=S△OBC=S正方形ABCD=
×1×1=
.
对接中考
2
解:∵∠ABO=90°,∠A=30°,∴∠AOB=60°,
①若是顺时针旋150°,如图(1),点
A′
在
y
轴负半轴,
则
OA′=OA=4,
所以,点
A′
的坐标为(0,-4);
如图,在△AOB中,AB⊥OB,∠A=30°
,OA=4
,将△OAB绕点O旋转150°得△OA'B',则点A'的坐标为
.
如图,在△AOB中,AB⊥OB,∠A=30°
,OA=4
,将△OAB绕点O旋转150°得△OA'B',则点A'的坐标为
.
对接中考
2
(0,-4)或(-2,-2)
解:②若是逆时针旋转150°,如图(2),
∵旋转角为150°,∴OA′
与
x
轴负半轴夹角为30°,
过点
A′
作A′C⊥x
轴于点C,则
A′C=OA′=
×4=2,
由勾股定理得,OC===2,
所以,点
A′
的坐标为(-2,-2),
综上所述,点
A′
的坐标为(0,-4)或(-2,-2).
对接中考
3
如图,等边三角形ABC内有一点O,已知OA=4,
OB=3,OC=5.求∠AOB的度数.
解:将△BOA绕点B顺时针旋转60°得△BPC,连接OP,如图,
由旋转的性质得BP=BO,∠OBP=60°.
∴△OBP
为等边三角形,
∴OP=OB=3.
由旋转的性质得PC=OA=4.
∵在△OPC
中,OP2+PC2=32+42
=OC2.
∴∠OPC=90°,∴∠CPB=∠OPB+∠OPC=60°+90°=150°,
∵旋转后的图形与旋转前的图形全等,∴∠AOB=∠CPB=150°.
23.1
第1课时
图形的旋转
知识回顾
同学们都见过风车吧,它能在风的吹动下不停地转动.在我们周围,还能看到许多转动着的物体,如车轮、水车、风力发电机、飞机的螺旋桨、时钟的指针、游乐园的大转盘……我们就生活在一个处处能见到旋转现象的世界中.
学习目标
1.掌握旋转的有关概念及基本性质.
2.能够根据旋转的基本性质解决实际问题.
课堂导入
在数学中,旋转是图形变化的方法之一,应该怎样描述它呢?它又有什么性质呢?本章将解答这些问题.
让我们一起来探索旋转的奥秘吧!
知识点1
新知探究
如图1,钟表的指针在不停的转动,从3时到5时,时针转动了多少度?
如图2,风车风轮的每个叶片在风的吹动下转动到新的位置.
图1
图2
以上这些现象有什么共同特点呢?
知识点1
新知探究
在平面内,将一个平面图形绕平面内某一点O转动一个角度,叫做图形的旋转.
O
P′
P
旋转中心
旋转角
对应点
点O叫做旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
初中阶段研究的平移、轴对称和旋转都是针对平面内的图形变换,它们是平面图形的全等变换.描述旋转时不能忽略“平面内”.旋转的角度一般小于360°.
知识点1
新知探究
1.旋转中心在旋转的过程中是静止不动的,旋转中心可以在图形的外部,也可以在图形的内部,还可以在图形上.
2.将一个图形绕一个定点沿某个方向转动一个角度,意味着图形上每一个点同时按相同方向旋转相同的角度.
3.旋转的三要素:旋转中心,旋转角,旋转方向.
知识点1
新知探究
一个图形由一个位置旋转到另一个位置,固定不动的点就是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
跟踪训练
新知探究
如图,A,B,C三点共线,△ACD和△BCE都是等边三角形,△ACE旋转后到达△DCB的位置.
(1)
旋转中心是哪一点?
(2)
旋转角是多少度?
(1)
点C是在△ACE旋转过程中不动的点,所以点C是旋转中心.
(2)
△ACE旋转后到达△DCB的位置,AC绕点C转过的角即∠ACD就是旋转角.因为△ACD是等边三角形,所以∠ACD
=60°,即旋转角是60°.
知识点2
新知探究
如图,在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△
),移开硬纸板.
△
是由△ABC绕点O旋转得到的.线
段OA与OA′有什么关系?∠AOA′与∠BOB′有什么关系?
△ABC与△
的形状和大小有什么关系?
知识点2
新知探究
A
B
C
B′
C′
O
A
B
C
·
A′
B′
C′
旋转前、后的图形全等,即对应角相等,对应边相等.
对应点到旋转中心的距离相等.
知识点2
新知探究
B'
A'
C'
A
B
C
O
线:
AO=A'O
,BO=B'O
,CO=C'O
角:∠AOA'=∠BOB'
=∠COC'
观察下图,你能得到什么结论?
知识点2
新知探究
(1)
旋转不改变图形的形状和大小,只改变图形的位置;
(2)
旋转时,图形上的每一点都绕旋转中心旋转相同的角度;
(3)
旋转的性质中所说的“对应点”是指“任意一对对应点”,并且对应点到旋转中心的距离相等.
知识点2
新知探究
旋转中心的确定
根据旋转的性质可知,对应点到旋转中心的距离相等,所以旋转中心位于对应点连线的垂直平分线上,即旋转中心是两对对应点所连线段的垂直平分线的交点.
跟踪训练
新知探究
如图,将△ABC
绕点A逆时针旋转得到△ADE,点C
和点E是对应点,若∠CAE=90°,AB=1,则BD=
.
解:将△ABC
绕点
A
逆时针旋转得到△ADE,点
C
和点
E
是对应点,
所以
AB=AD=1,∠BAD=∠CAE=90°,
所以
BD=.
随堂练习
1
如图,在边长为1的正方形网格中,将△ABC绕点P顺时针旋转90°得到△A′B′C′
,则点P的坐标是(
)
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
B
解:∵将△ABC以点P为旋转中心,顺时针旋转90°得到△A′B′C′,
∴点A的对应点为点A′,点C的对应点为点C′,
作线段AA′和CC′的垂直平分线,它们的交点为(1,2),
∴点P的坐标为(1,2).
P
如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°
,则CD的长为(
)
A.0.5
B.1.5
C.
D.1
随堂练习
2
D
解:∵∠BAC=90°,∠B=60°,∴BC=2AB=2,
∵Rt△ABC
绕点
A
按顺时针旋转一定角度得到Rt△ADE,
点
B
的对应点
D
恰好落在
BC
边上,
∴AD=AB,
而∠B=60°,∴△ABD
为等边三角形,
∴BD=AB=1,∴CD=BC-BD=2-1=1.
随堂练习
3
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB'C'
的位置,使得
CC′
//AB,则∠BAB′
的度数是(
)
A.30°
B.35°
C.40°
D.50°
A
解:∵CC′∥AB,∠CAB=75°,
∴∠C′CA=∠CAB=75°,
又∵C,C′
为对应点,点
A
为旋转中心,
∴AC=AC′,即△ACC′
为等腰三角形,
∴∠BAB′=∠CAC′=180°-2∠C′CA=30°.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
对接中考
1
如图,正方形ABCD和正方形EFGO的边长都是1,正方形EFGO绕点O旋转时,两个正方形重叠部分的面积是(
)
A.
B.
C.
D.不能确定
A
解:∵四边形
ABCD
和四边形
EFGO
都是正方形,
∴OB=OC,∠OBC=∠OCB=45°,∠BOC=∠EOG=90°,
∴∠BON=∠COM.
在△OBN
与△OCM
中,
∴△OBN≌△OCM(ASA),∴S△OBN=S△OCM,
∴S四边形OMBN=S△OBC=S正方形ABCD=
×1×1=
.
对接中考
2
解:∵∠ABO=90°,∠A=30°,∴∠AOB=60°,
①若是顺时针旋150°,如图(1),点
A′
在
y
轴负半轴,
则
OA′=OA=4,
所以,点
A′
的坐标为(0,-4);
如图,在△AOB中,AB⊥OB,∠A=30°
,OA=4
,将△OAB绕点O旋转150°得△OA'B',则点A'的坐标为
.
如图,在△AOB中,AB⊥OB,∠A=30°
,OA=4
,将△OAB绕点O旋转150°得△OA'B',则点A'的坐标为
.
对接中考
2
(0,-4)或(-2,-2)
解:②若是逆时针旋转150°,如图(2),
∵旋转角为150°,∴OA′
与
x
轴负半轴夹角为30°,
过点
A′
作A′C⊥x
轴于点C,则
A′C=OA′=
×4=2,
由勾股定理得,OC===2,
所以,点
A′
的坐标为(-2,-2),
综上所述,点
A′
的坐标为(0,-4)或(-2,-2).
对接中考
3
如图,等边三角形ABC内有一点O,已知OA=4,
OB=3,OC=5.求∠AOB的度数.
解:将△BOA绕点B顺时针旋转60°得△BPC,连接OP,如图,
由旋转的性质得BP=BO,∠OBP=60°.
∴△OBP
为等边三角形,
∴OP=OB=3.
由旋转的性质得PC=OA=4.
∵在△OPC
中,OP2+PC2=32+42
=OC2.
∴∠OPC=90°,∴∠CPB=∠OPB+∠OPC=60°+90°=150°,
∵旋转后的图形与旋转前的图形全等,∴∠AOB=∠CPB=150°.
同课章节目录
