人教版九年级数学上册23.2.2 中心对称图形课件(18张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.2.2 中心对称图形课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 522.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 20:01:22 | ||
图片预览





文档简介
(共18张PPT)
23.2.2
中心对称图形
中心对称
知识回顾
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
学习目标
1.会识别中心对称图形.
2.会运用中心对称图形的性质解决实际问题.
课堂导入
我们上节课学习了中心对称的相关知识,中心对称是指两个图形的关系,而把这两个图形看作一个整体是什么图形呢?是我们这节课所要学习的中心对称图形.
知识点1
新知探究
(1)如图,将线段AB绕它的中点旋转180°,你有什么发现?
A
B
线段AB绕它的中点旋转180°后与它本身重合.
知识点1
新知探究
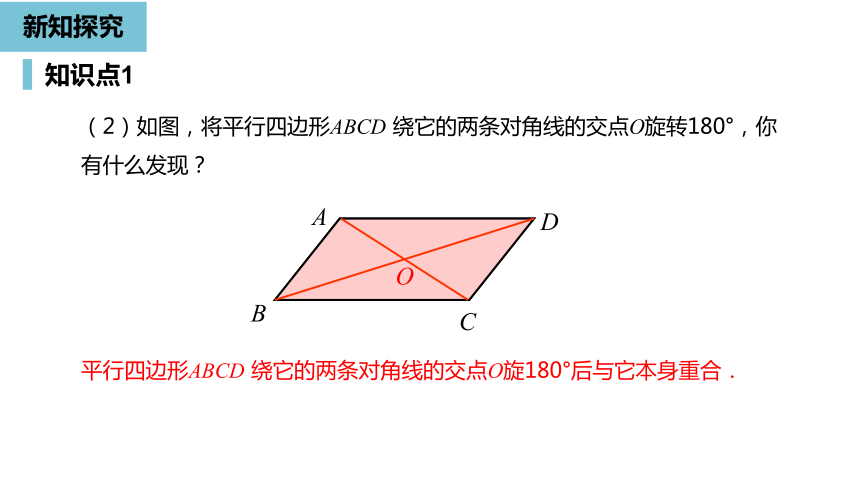
(2)如图,将平行四边形ABCD
绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
平行四边形ABCD
绕它的两条对角线的交点O旋180°后与它本身重合.
知识点1
新知探究
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
知识点1
新知探究
中心对称与中心对称图形的区别与联系
中心对称
中心对称图形
区别
(1)
是针对两个图形而言的
(2)
是指两个图形的(位置)关系
(3)
对称点在两个图形上
(4)
对称中心可能在两个图形的外部,也可能在图形的内部或图形上
(1)
是针对一个图形而言的
(2)
是指具有某种性质的一个图形
(3)
对称点在一个图形上
(4)
对称中心在图形内部
联系
(1)
都是根据把图形旋转180°后能重合定义的.
(2)
两者可以相互转化,若把成中心对称的两个图形视为一个整体,则整个图形是中心对称图形;若把一个中心对称图形相互对称的两部分看作两个图形,则这两个图形成中心对称.
知识点1
新知探究
中心对称图形的性质
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分,即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等).
跟踪训练
新知探究
下列图形中是中心对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
B
解:4个图形中只有平行四边形和正六边形是中心对称图形.
平行四边形
正六边形
正五边形
正三角形
随堂练习
1
下列图形中,既是中心对称图形又是轴对称图形的有(
)
D
A.4个
B.3个
C.2个
D.1个
解:第一个图形既是中心对称图形又是轴对称图形;
第二个图形是轴对称图形,不是中心对称图形;
第三个图形是中心对称图形,不是轴对称图形;
第四个图形是轴对称图形,不是中心对称图形.
随堂练习
2
在下列图形中,既是轴对称图形,又是中心对称图形的是(
)
A.等边三角形
B.直角三角形
C.正方形
D.五边形
解:等边三角形是轴对称图形,不是中心对称图形,故A选项错误;
直角三角形不一定是轴对称图形,也不是中心对称图形,故B选项错误;
正方形是轴对称图形,也是中心对称图形,故C选项正确;
五边形是轴对称图形,但不是中心对称图形,故D选项错误.
C
随堂练习
3
下图中所有的小正方形都全等,将图(1)的小正方形放在图(2)中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是(
)
C
A.①
B.②
C.③
D.④
课堂小结
中心对称图形
定义
性质
应用
绕着内部一点旋转180°能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
对接中考
1
下列图形可以看作中心对称图形的是(
)
B
解:根据中心对称图形的概念“把一个图形绕着某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形”可知选项B是中心对称图形.
对接中考
2
近几年我国国产汽车行业蓬勃发展,下列汽车标识中,是中心对称图形的是(
)
D
A
B
C
D
对接中考
3
B
下列图形中,既是中心对称图形又是轴对称图形的有(
)
解:选项A中的图形是轴对称图形,但不是中心对称图形;
选项B中的图形既是轴对称图形又是中心对称图形;
选项C,D中的图形是中心对称图形,但不是轴对称图形,
故选B.
对接中考
4
有4张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180°后得到的图形如图(2)所示,那么她所旋转的牌从左起是(
)
A
A.第一张或第二张
B.第二张或第三张
C.第三张或第四张
D.第一张或第四张
23.2.2
中心对称图形
中心对称
知识回顾
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
学习目标
1.会识别中心对称图形.
2.会运用中心对称图形的性质解决实际问题.
课堂导入
我们上节课学习了中心对称的相关知识,中心对称是指两个图形的关系,而把这两个图形看作一个整体是什么图形呢?是我们这节课所要学习的中心对称图形.
知识点1
新知探究
(1)如图,将线段AB绕它的中点旋转180°,你有什么发现?
A
B
线段AB绕它的中点旋转180°后与它本身重合.
知识点1
新知探究
(2)如图,将平行四边形ABCD
绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
平行四边形ABCD
绕它的两条对角线的交点O旋180°后与它本身重合.
知识点1
新知探究
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
知识点1
新知探究
中心对称与中心对称图形的区别与联系
中心对称
中心对称图形
区别
(1)
是针对两个图形而言的
(2)
是指两个图形的(位置)关系
(3)
对称点在两个图形上
(4)
对称中心可能在两个图形的外部,也可能在图形的内部或图形上
(1)
是针对一个图形而言的
(2)
是指具有某种性质的一个图形
(3)
对称点在一个图形上
(4)
对称中心在图形内部
联系
(1)
都是根据把图形旋转180°后能重合定义的.
(2)
两者可以相互转化,若把成中心对称的两个图形视为一个整体,则整个图形是中心对称图形;若把一个中心对称图形相互对称的两部分看作两个图形,则这两个图形成中心对称.
知识点1
新知探究
中心对称图形的性质
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分,即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等).
跟踪训练
新知探究
下列图形中是中心对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
B
解:4个图形中只有平行四边形和正六边形是中心对称图形.
平行四边形
正六边形
正五边形
正三角形
随堂练习
1
下列图形中,既是中心对称图形又是轴对称图形的有(
)
D
A.4个
B.3个
C.2个
D.1个
解:第一个图形既是中心对称图形又是轴对称图形;
第二个图形是轴对称图形,不是中心对称图形;
第三个图形是中心对称图形,不是轴对称图形;
第四个图形是轴对称图形,不是中心对称图形.
随堂练习
2
在下列图形中,既是轴对称图形,又是中心对称图形的是(
)
A.等边三角形
B.直角三角形
C.正方形
D.五边形
解:等边三角形是轴对称图形,不是中心对称图形,故A选项错误;
直角三角形不一定是轴对称图形,也不是中心对称图形,故B选项错误;
正方形是轴对称图形,也是中心对称图形,故C选项正确;
五边形是轴对称图形,但不是中心对称图形,故D选项错误.
C
随堂练习
3
下图中所有的小正方形都全等,将图(1)的小正方形放在图(2)中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是(
)
C
A.①
B.②
C.③
D.④
课堂小结
中心对称图形
定义
性质
应用
绕着内部一点旋转180°能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
对接中考
1
下列图形可以看作中心对称图形的是(
)
B
解:根据中心对称图形的概念“把一个图形绕着某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形”可知选项B是中心对称图形.
对接中考
2
近几年我国国产汽车行业蓬勃发展,下列汽车标识中,是中心对称图形的是(
)
D
A
B
C
D
对接中考
3
B
下列图形中,既是中心对称图形又是轴对称图形的有(
)
解:选项A中的图形是轴对称图形,但不是中心对称图形;
选项B中的图形既是轴对称图形又是中心对称图形;
选项C,D中的图形是中心对称图形,但不是轴对称图形,
故选B.
对接中考
4
有4张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180°后得到的图形如图(2)所示,那么她所旋转的牌从左起是(
)
A
A.第一张或第二张
B.第二张或第三张
C.第三张或第四张
D.第一张或第四张
同课章节目录
