人教版九年级数学上册23.2.3关于原点对称的点的坐标课件(19张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.2.3关于原点对称的点的坐标课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 164.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 20:02:19 | ||
图片预览





文档简介
(共19张PPT)
23.2.3
关于原点对称的点的坐标
中心对称
知识回顾
下列各点分别在坐标平面的什么位置上?
A(3,2)
B(
0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
学习目标
1.掌握两点关于原点对称时,横纵坐标的关系.
2.会在平面直角坐标系内作关于原点对称的图形.
3.进一步体会数形结合的思想.
课堂导入
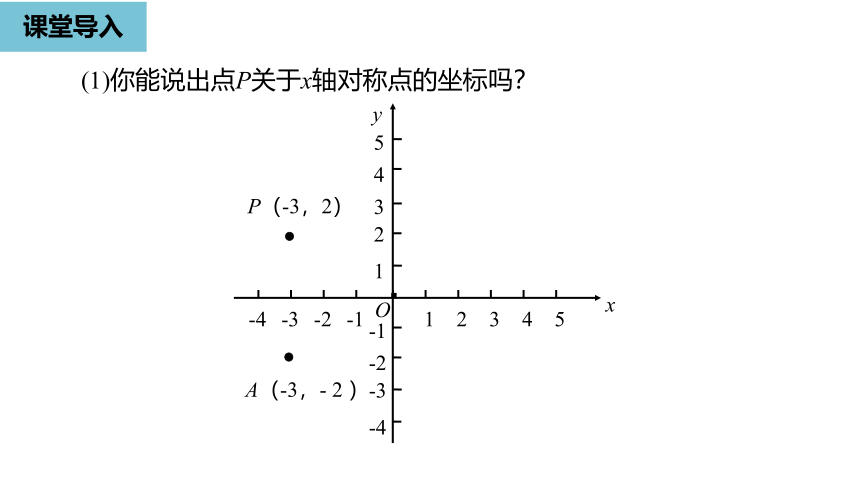
P(-3,2)
A(-3,-
2
)
(1)你能说出点P关于x轴对称点的坐标吗?
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
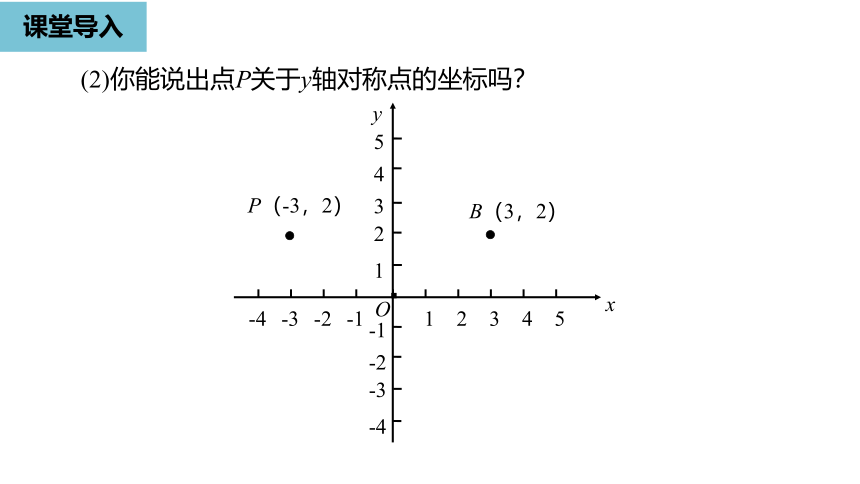
B(3,2)
P(-3,2)
(2)你能说出点P关于y轴对称点的坐标吗?
课堂导入
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
C(3,-2)
A(-3,-
2
)
点A与点B的位置关系是怎样的?点P与点C呢?
课堂导入
B(3,2)
P(-3,2)
知识点1
新知探究
在直角坐标系中,作出下列点关于原点的对称点,并写出它们的坐标.
关于原点对称的两个点的坐标之间有什么关系?
A(4,0)
B(0,-3)
C(2,1)
D(-1,2)
E(-3,-4)
点A,B,C,D
关于原点的对称点的坐标分别为:
(-4,0)
(0,3)
(-2,-1)
(1,-2)
(3,4)
知识点1
新知探究
两个点关于原点对称时,它们的坐标符号相反.
简记为:“关于谁,谁不变,关于原点都改变”.
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a,
b).
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
知识点1
新知探究
例
如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
·
A
C
B
A′
C′
B′
解:△ABC的三个顶点的坐标分别为A(-4,1),B(-1,
-1),C(-3,2),
A′(4,-1),B′(1,1),C′(3,-2)
关于原点的对称点的坐标分别为
依次连接A′B′
,B′C′
,C′
A′
,
就可得到与△ABC关于原点对称的
△A′B′C′
.
知识点1
新知探究
作关于原点对称的图形的步骤:
(1)
写出图形各顶点的坐标;
(2)
写出图形各顶点关于原点的对称点的坐标;
(3)
描点;
(4)
顺次连接;
(5)
下结论.
跟踪训练
新知探究
在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab=
.
12
解:∵点
A
的坐标为(a,3),
点
B
的坐标是(4,b),
点
A
与点
B
关于原点
O
对称,
∴a=-4,b=-3,
则
ab=12.
随堂练习
1
下列各点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D(2,0),E(0,5),F(-2,1),G(-2,-1).
解:点
C
与点
F
的横纵坐标分别互为相反数,
所以点
C
与点
F关于原点
O
对称.
随堂练习
2
若点M(3,a-2),N(b,a)关于原点对称,则a
+
b=
.
-2
解:由题意,得
b=-3,a-2+a=0,
解得
a=1,
∴a
+
b
=
-3
+
1
=
-2.
随堂练习
3
在平面直角坐标系中,第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,则x+2y=
.
-7
解:根据题意,得
(x2+2x)+(x+2)=0,y=-3,
∴x1=-1,x2=-2(不符合题意,舍去).
∴x=-1,y=-3
∴x+2y=-7.
课堂小结
关于原点对称的点的坐标
特征
P(x,y)关于原点的对称点为P'(-x,-y).
作图
作关于原点对称的图形,先求出对称点的坐标再描点画图.
对接中考
1
在平面直角坐标系中,点P(-3,
-5)关于原点对称的点的坐标是(
)
C
A.
(3,
-5)
B.(
-3,5)
C.
(3,5)
D.(
-3,-5)
(2019·安顺中考)在平面直角坐标系中,点P(?3,m?+1)关于原点的对称点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
对接中考
2
解:点P关于原点对称的点的坐标为(3,?(m?+1)),
∵m?+1
>0,
∴?(
m?+1)<0,
故点P关于原点的对称点在第四象限.
D
对接中考
3
写出下列各点关于原点的对称点的坐标.
A(3,1),B(-2,3),C(-1,-2),D(2,-3).
(-3,-1)
(2,-3)
(1,2)
(-2,3).
对接中考
4
在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-
300°)或P(3
,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是(
)
D
Q(3,240°)
Q(3,-
120°)
C.
Q(3,600°)
D.
Q(3,
-500°)
23.2.3
关于原点对称的点的坐标
中心对称
知识回顾
下列各点分别在坐标平面的什么位置上?
A(3,2)
B(
0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
学习目标
1.掌握两点关于原点对称时,横纵坐标的关系.
2.会在平面直角坐标系内作关于原点对称的图形.
3.进一步体会数形结合的思想.
课堂导入
P(-3,2)
A(-3,-
2
)
(1)你能说出点P关于x轴对称点的坐标吗?
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
B(3,2)
P(-3,2)
(2)你能说出点P关于y轴对称点的坐标吗?
课堂导入
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
C(3,-2)
A(-3,-
2
)
点A与点B的位置关系是怎样的?点P与点C呢?
课堂导入
B(3,2)
P(-3,2)
知识点1
新知探究
在直角坐标系中,作出下列点关于原点的对称点,并写出它们的坐标.
关于原点对称的两个点的坐标之间有什么关系?
A(4,0)
B(0,-3)
C(2,1)
D(-1,2)
E(-3,-4)
点A,B,C,D
关于原点的对称点的坐标分别为:
(-4,0)
(0,3)
(-2,-1)
(1,-2)
(3,4)
知识点1
新知探究
两个点关于原点对称时,它们的坐标符号相反.
简记为:“关于谁,谁不变,关于原点都改变”.
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a,
b).
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
知识点1
新知探究
例
如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
·
A
C
B
A′
C′
B′
解:△ABC的三个顶点的坐标分别为A(-4,1),B(-1,
-1),C(-3,2),
A′(4,-1),B′(1,1),C′(3,-2)
关于原点的对称点的坐标分别为
依次连接A′B′
,B′C′
,C′
A′
,
就可得到与△ABC关于原点对称的
△A′B′C′
.
知识点1
新知探究
作关于原点对称的图形的步骤:
(1)
写出图形各顶点的坐标;
(2)
写出图形各顶点关于原点的对称点的坐标;
(3)
描点;
(4)
顺次连接;
(5)
下结论.
跟踪训练
新知探究
在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab=
.
12
解:∵点
A
的坐标为(a,3),
点
B
的坐标是(4,b),
点
A
与点
B
关于原点
O
对称,
∴a=-4,b=-3,
则
ab=12.
随堂练习
1
下列各点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D(2,0),E(0,5),F(-2,1),G(-2,-1).
解:点
C
与点
F
的横纵坐标分别互为相反数,
所以点
C
与点
F关于原点
O
对称.
随堂练习
2
若点M(3,a-2),N(b,a)关于原点对称,则a
+
b=
.
-2
解:由题意,得
b=-3,a-2+a=0,
解得
a=1,
∴a
+
b
=
-3
+
1
=
-2.
随堂练习
3
在平面直角坐标系中,第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,则x+2y=
.
-7
解:根据题意,得
(x2+2x)+(x+2)=0,y=-3,
∴x1=-1,x2=-2(不符合题意,舍去).
∴x=-1,y=-3
∴x+2y=-7.
课堂小结
关于原点对称的点的坐标
特征
P(x,y)关于原点的对称点为P'(-x,-y).
作图
作关于原点对称的图形,先求出对称点的坐标再描点画图.
对接中考
1
在平面直角坐标系中,点P(-3,
-5)关于原点对称的点的坐标是(
)
C
A.
(3,
-5)
B.(
-3,5)
C.
(3,5)
D.(
-3,-5)
(2019·安顺中考)在平面直角坐标系中,点P(?3,m?+1)关于原点的对称点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
对接中考
2
解:点P关于原点对称的点的坐标为(3,?(m?+1)),
∵m?+1
>0,
∴?(
m?+1)<0,
故点P关于原点的对称点在第四象限.
D
对接中考
3
写出下列各点关于原点的对称点的坐标.
A(3,1),B(-2,3),C(-1,-2),D(2,-3).
(-3,-1)
(2,-3)
(1,2)
(-2,3).
对接中考
4
在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-
300°)或P(3
,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是(
)
D
Q(3,240°)
Q(3,-
120°)
C.
Q(3,600°)
D.
Q(3,
-500°)
同课章节目录
