人教版九年级数学上册24.1.4圆周角课件(24张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.4圆周角课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 706.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 20:15:22 | ||
图片预览



文档简介
(共24张PPT)
24.1.4
圆周角
圆的有关性质
知识回顾
什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角,
∠AOB.
学习目标
2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.
1.理解圆周角的概念,会叙述并证明圆周角定理.
3.理解掌握圆周角定理的推论及其证明过程和运用.
课堂导入
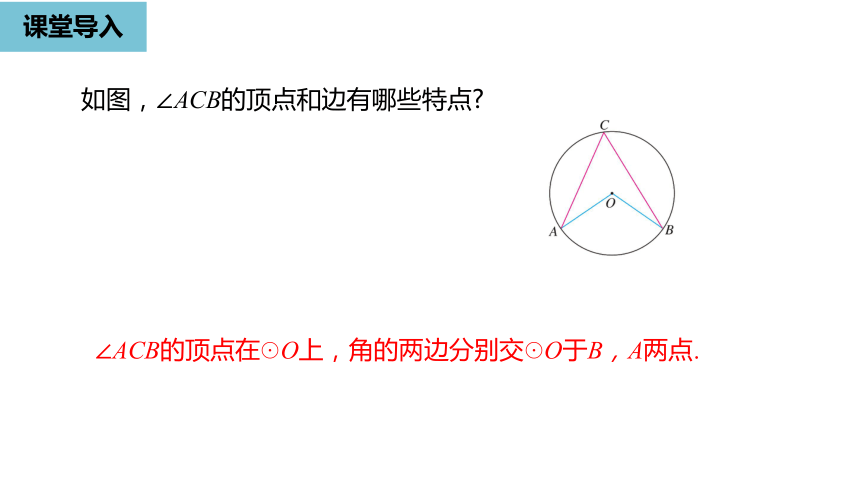
如图,∠ACB的顶点和边有哪些特点?
∠ACB的顶点在☉O上,角的两边分别交☉O于B,A两点.
知识点1
新知探究
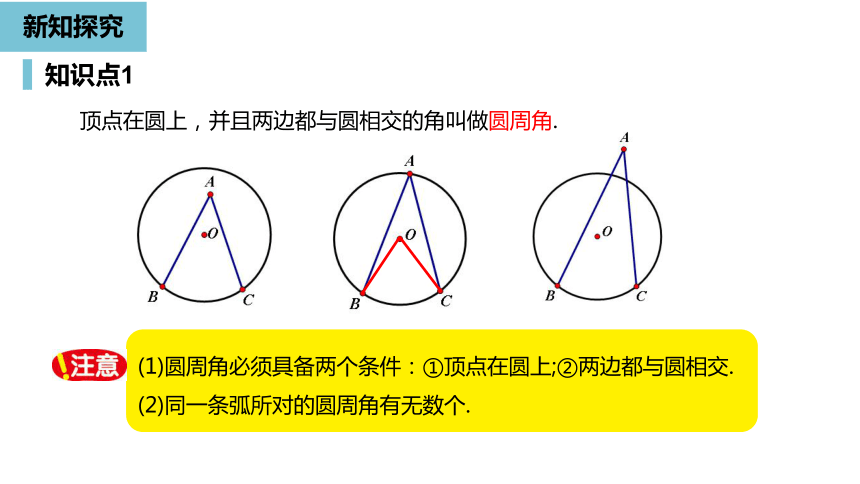
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(1)圆周角必须具备两个条件:①顶点在圆上;②两边都与圆相交.
(2)同一条弧所对的圆周角有无数个.
知识点1
新知探究
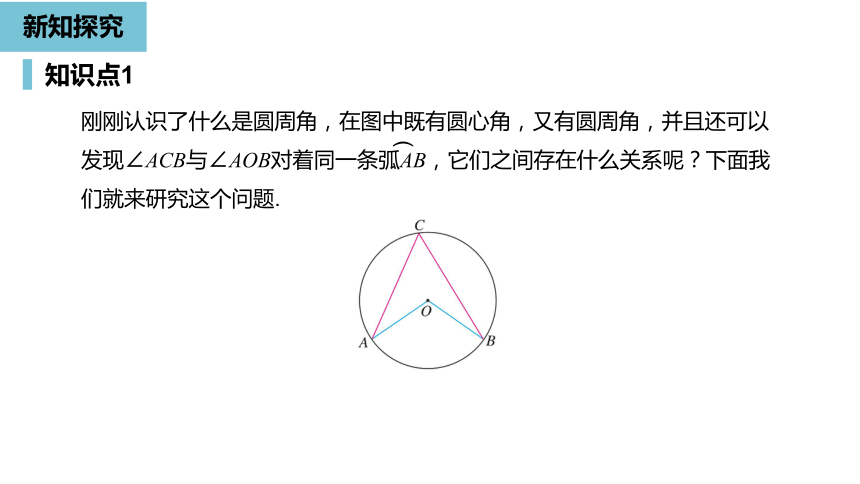
刚刚认识了什么是圆周角,在图中既有圆心角,又有圆周角,并且还可以发现∠ACB与∠AOB对着同一条弧AB,它们之间存在什么关系呢?下面我们就来研究这个问题.
(
知识点1
新知探究
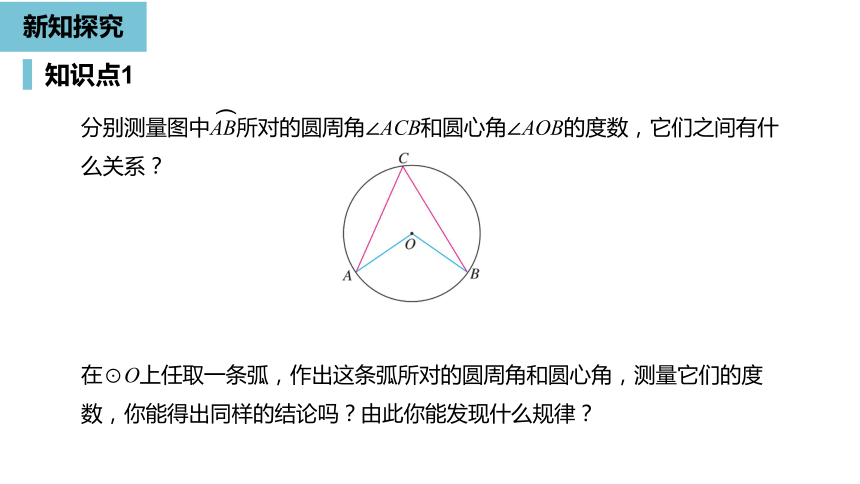
分别测量图中AB所对的圆周角∠ACB和圆心角∠AOB的度数,它们之间有什么关系?
(
在⊙O上任取一条弧,作出这条弧所对的圆周角和圆心角,测量它们的度数,你能得出同样的结论吗?由此你能发现什么规律?
知识点1
新知探究
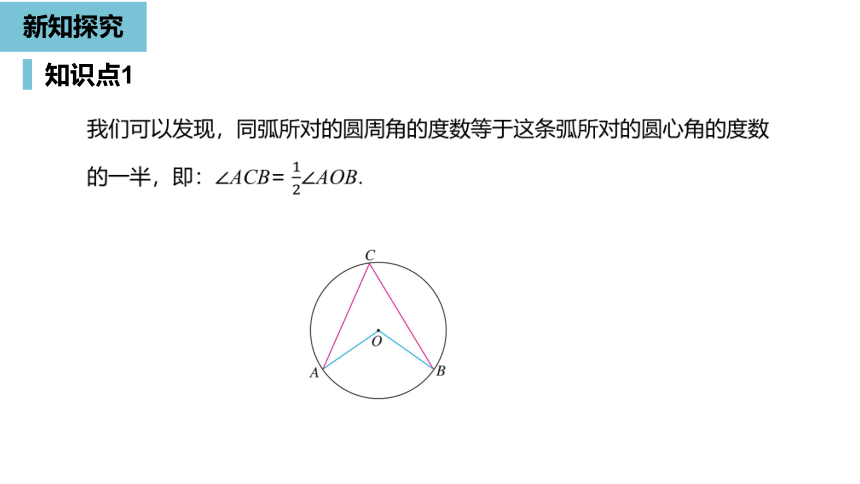
我们可以发现,同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半,即:∠ACB=
∠AOB.
知识点1
新知探究
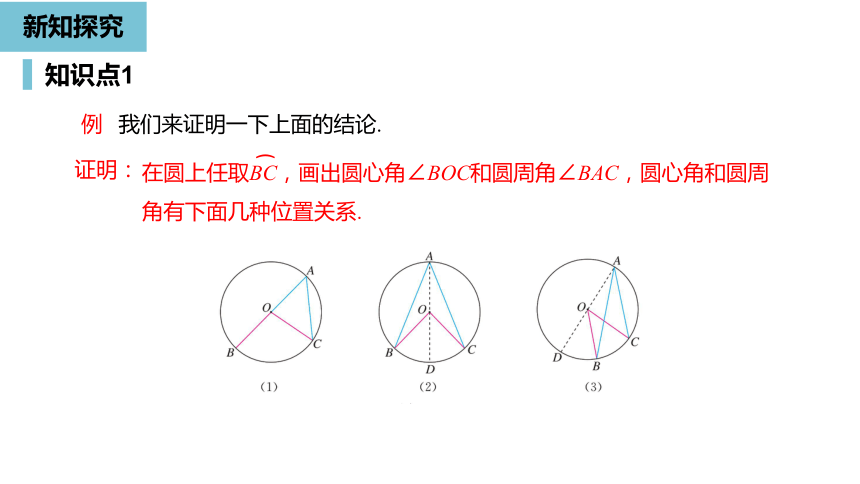
例
我们来证明一下上面的结论.
在圆上任取BC,画出圆心角∠BOC和圆周角∠BAC,圆心角和圆周角有下面几种位置关系.
(
证明:
知识点1
新知探究
对于第(2)(3)种情况,可以通过添加辅助线(图(2)(3)),将它们转化为第(1)种情况.从而得到相同的结论(请你自己完成证明).
我们来分析第(1)种情况,如图(1),圆心O在∠BAC的一条边上.
知识点1
新知探究
如图,OB,OC都是⊙O的半径,点A,D
是圆上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.
D
解:∠BAC=
∠BOC,
∠BDC
=
∠BOC,
所以∠BAC=∠BDC.
知识点1
新知探究
D
A
B
O
C
E
F
(1)如图,若
CD=EF
,∠A与∠B相等吗?
(
(
解:因为CD=EF
,
所以∠COD=∠EOF,
又∠A=
∠COD,
∠B=∠EOF,
所以
∠A
∠B.
(
(
知识点1
新知探究
解:因为∠A=∠B,∠A=
∠COD,
∠B=∠EOF,
所以∠COD=∠EOF,
所以
CDEF.
(2)
反过来,若∠A=∠B,那么
CDEF成立吗?
(
(
(
(
D
A
B
O
C
E
F
知识点1
新知探究
同弧或等弧所对的圆周角相等.
A1
A2
A3
圆周角定理的推论
知识点1
新知探究
如图,线段AB是☉O的直径,点C是
☉O上的任意一点(除点A、B外),那么,∠ACB就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
·
O
A
C
B
解:∵OA=OB=OC,
∴△AOC、△BOC都是等腰三角形.
∴
∠OAC=∠OCA,∠OBC=∠OCB.
又∵
∠OAC+∠OBC+∠ACB=180°,
∴
∠ACB=∠OCA+∠OCB=180°÷2=90°.
知识点1
新知探究
圆周角和直径的关系:
半圆或直径所对的圆周角都相等,都等于90°.
知识点1
新知探究
例
如图(1),⊙O
的直径
AB
为
10
cm,弦
AC为
6
cm,∠ACB
的平分线交⊙O于D,求BC,AD,BD的长.
解:如图(2),连接OD,
∵AB
是直径,∴
∠ACB=
∠ADB=
90°.
在
Rt△ABC中,BC=
在Rt△ABD中,AD2+BD2=AB2,
∵CD平分∠ACB,∴∠ACD=∠BCD.
∴
∠AOD=∠BOD,∴AD=BD.
图(1)
图(2)
跟踪训练
新知探究
如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是(
)
A
A.58°
B.60°
C.64°
D.68°
解:∵OA=OC,
∴∠C=∠OAC=32°,
∵BC是直径,
∴∠B=90°-32°=58°.
随堂练习
1
判断下列图形中的角是不是圆周角,并说明理由.
×
×
√
×
×
随堂练习
2
如图,
A,B,C,D是⊙O上的四个点,B是
的中点,M是半径OD上任意一点,若∠BDC=40°,则∠AMB的度数不可能是(
)
A.45°
B.60°
C.75°
D.85°
D
解:连接AO,BO,
∵B是的中点,
∴∠AOB=2∠BDC=80°,
又M是OD上一点,
∴∠AMB≤∠AOB=80°,
则不符合条件的只有85°.
随堂练习
3
如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为(
)
B
A.100°
B.110°
C.115°
D.120°
解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠AED=20°,
∴∠ACD=20°,
∴∠BCD=∠ACB+∠ACD=110°.
课堂小结
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
90°的圆周角所对的弦是直径.
1.顶点在圆上,
2.两边都与圆相交的角(二者必须同时具备).
圆周角与直
径的关系
半圆或直径所对的圆周角都相等,都等于90°(直角).
对接中考
1
如图,⊙O的半径OD⊥AB于点C,连接AO并延长,交⊙O于点E,连接EC.若AB=8,CD=2,则CE的长为(
)
D
A.2
B.8
C.2
D.2
解:连接BE,设⊙O半径为r,则OA=OD=r,OC=r-2,
∵OD⊥AB,∴∠ACO=90°,AC=BC=AB=4,
在Rt△ACO中,由勾股定理得:r2=42+(r-2)2,
解得r=5,∴AE=2r=10,
∵AE为⊙O的直径,∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中,CE==2.
对接中考
2
如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,
∠ACE的度数为
.
30°
解:如图,连接OC,∵AB是直径,
,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC,
∴△AOC是等边三角形,∴∠A=60°,
∵CE⊥OA,∴∠AEC=90°,
∴∠ACE=90°-60°=30°.
24.1.4
圆周角
圆的有关性质
知识回顾
什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角,
∠AOB.
学习目标
2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.
1.理解圆周角的概念,会叙述并证明圆周角定理.
3.理解掌握圆周角定理的推论及其证明过程和运用.
课堂导入
如图,∠ACB的顶点和边有哪些特点?
∠ACB的顶点在☉O上,角的两边分别交☉O于B,A两点.
知识点1
新知探究
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(1)圆周角必须具备两个条件:①顶点在圆上;②两边都与圆相交.
(2)同一条弧所对的圆周角有无数个.
知识点1
新知探究
刚刚认识了什么是圆周角,在图中既有圆心角,又有圆周角,并且还可以发现∠ACB与∠AOB对着同一条弧AB,它们之间存在什么关系呢?下面我们就来研究这个问题.
(
知识点1
新知探究
分别测量图中AB所对的圆周角∠ACB和圆心角∠AOB的度数,它们之间有什么关系?
(
在⊙O上任取一条弧,作出这条弧所对的圆周角和圆心角,测量它们的度数,你能得出同样的结论吗?由此你能发现什么规律?
知识点1
新知探究
我们可以发现,同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半,即:∠ACB=
∠AOB.
知识点1
新知探究
例
我们来证明一下上面的结论.
在圆上任取BC,画出圆心角∠BOC和圆周角∠BAC,圆心角和圆周角有下面几种位置关系.
(
证明:
知识点1
新知探究
对于第(2)(3)种情况,可以通过添加辅助线(图(2)(3)),将它们转化为第(1)种情况.从而得到相同的结论(请你自己完成证明).
我们来分析第(1)种情况,如图(1),圆心O在∠BAC的一条边上.
知识点1
新知探究
如图,OB,OC都是⊙O的半径,点A,D
是圆上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.
D
解:∠BAC=
∠BOC,
∠BDC
=
∠BOC,
所以∠BAC=∠BDC.
知识点1
新知探究
D
A
B
O
C
E
F
(1)如图,若
CD=EF
,∠A与∠B相等吗?
(
(
解:因为CD=EF
,
所以∠COD=∠EOF,
又∠A=
∠COD,
∠B=∠EOF,
所以
∠A
∠B.
(
(
知识点1
新知探究
解:因为∠A=∠B,∠A=
∠COD,
∠B=∠EOF,
所以∠COD=∠EOF,
所以
CDEF.
(2)
反过来,若∠A=∠B,那么
CDEF成立吗?
(
(
(
(
D
A
B
O
C
E
F
知识点1
新知探究
同弧或等弧所对的圆周角相等.
A1
A2
A3
圆周角定理的推论
知识点1
新知探究
如图,线段AB是☉O的直径,点C是
☉O上的任意一点(除点A、B外),那么,∠ACB就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
·
O
A
C
B
解:∵OA=OB=OC,
∴△AOC、△BOC都是等腰三角形.
∴
∠OAC=∠OCA,∠OBC=∠OCB.
又∵
∠OAC+∠OBC+∠ACB=180°,
∴
∠ACB=∠OCA+∠OCB=180°÷2=90°.
知识点1
新知探究
圆周角和直径的关系:
半圆或直径所对的圆周角都相等,都等于90°.
知识点1
新知探究
例
如图(1),⊙O
的直径
AB
为
10
cm,弦
AC为
6
cm,∠ACB
的平分线交⊙O于D,求BC,AD,BD的长.
解:如图(2),连接OD,
∵AB
是直径,∴
∠ACB=
∠ADB=
90°.
在
Rt△ABC中,BC=
在Rt△ABD中,AD2+BD2=AB2,
∵CD平分∠ACB,∴∠ACD=∠BCD.
∴
∠AOD=∠BOD,∴AD=BD.
图(1)
图(2)
跟踪训练
新知探究
如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是(
)
A
A.58°
B.60°
C.64°
D.68°
解:∵OA=OC,
∴∠C=∠OAC=32°,
∵BC是直径,
∴∠B=90°-32°=58°.
随堂练习
1
判断下列图形中的角是不是圆周角,并说明理由.
×
×
√
×
×
随堂练习
2
如图,
A,B,C,D是⊙O上的四个点,B是
的中点,M是半径OD上任意一点,若∠BDC=40°,则∠AMB的度数不可能是(
)
A.45°
B.60°
C.75°
D.85°
D
解:连接AO,BO,
∵B是的中点,
∴∠AOB=2∠BDC=80°,
又M是OD上一点,
∴∠AMB≤∠AOB=80°,
则不符合条件的只有85°.
随堂练习
3
如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为(
)
B
A.100°
B.110°
C.115°
D.120°
解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠AED=20°,
∴∠ACD=20°,
∴∠BCD=∠ACB+∠ACD=110°.
课堂小结
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
90°的圆周角所对的弦是直径.
1.顶点在圆上,
2.两边都与圆相交的角(二者必须同时具备).
圆周角与直
径的关系
半圆或直径所对的圆周角都相等,都等于90°(直角).
对接中考
1
如图,⊙O的半径OD⊥AB于点C,连接AO并延长,交⊙O于点E,连接EC.若AB=8,CD=2,则CE的长为(
)
D
A.2
B.8
C.2
D.2
解:连接BE,设⊙O半径为r,则OA=OD=r,OC=r-2,
∵OD⊥AB,∴∠ACO=90°,AC=BC=AB=4,
在Rt△ACO中,由勾股定理得:r2=42+(r-2)2,
解得r=5,∴AE=2r=10,
∵AE为⊙O的直径,∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中,CE==2.
对接中考
2
如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,
∠ACE的度数为
.
30°
解:如图,连接OC,∵AB是直径,
,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC,
∴△AOC是等边三角形,∴∠A=60°,
∵CE⊥OA,∴∠AEC=90°,
∴∠ACE=90°-60°=30°.
同课章节目录
