人教版九年级数学上册24.2.1点和圆的位置关系(1)课件(17张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.2.1点和圆的位置关系(1)课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 507.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
24.2.1点和圆的位置关系
点和圆、直线和圆的位置关系
知识回顾
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
圆的集合定义
学习目标
1.理解并掌握点和圆的三种位置关系.
2.经历探索点与圆的三种位置关系,体会数学分类讨论思考问题的方法.
课堂导入
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.下图是射击靶的示意图,它是由许多同心圆(圆心相同、半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
知识点1
新知探究
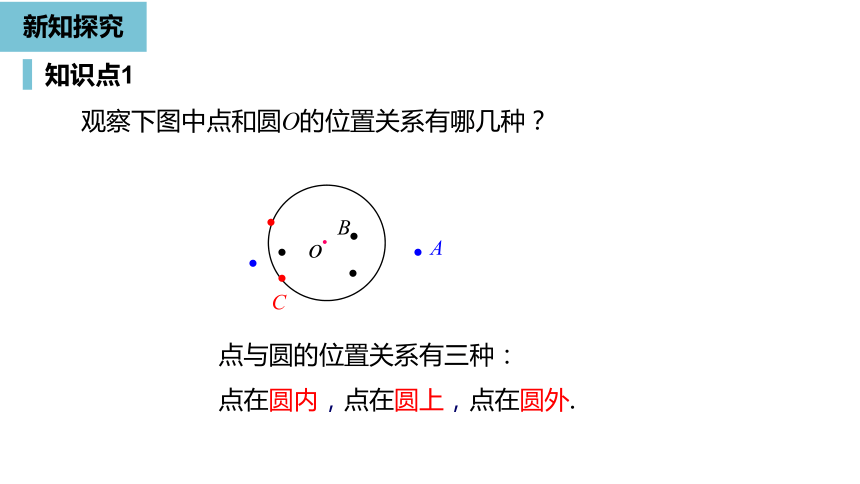
观察下图中点和圆O的位置关系有哪几种?
.
o
.
C
.
.
.
B
.
.A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
知识点1
新知探究
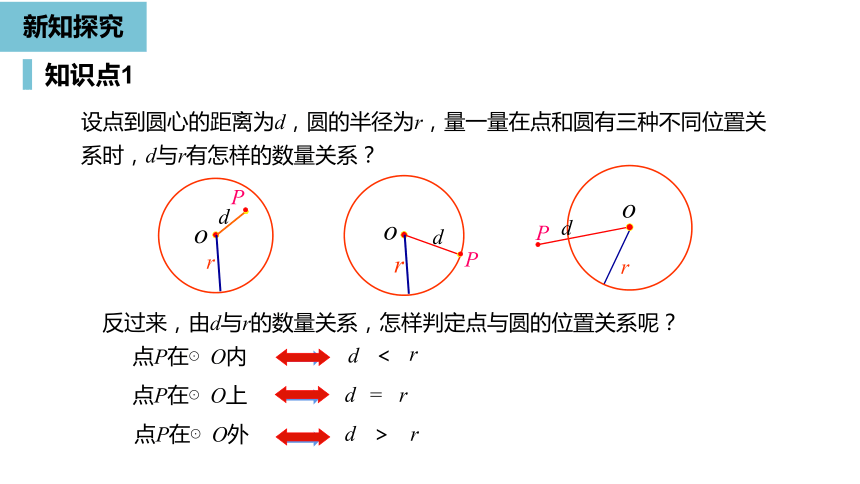
设点到圆心的距离为d,圆的半径为r,量一量在点和圆有三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
o
o
o
知识点1
新知探究
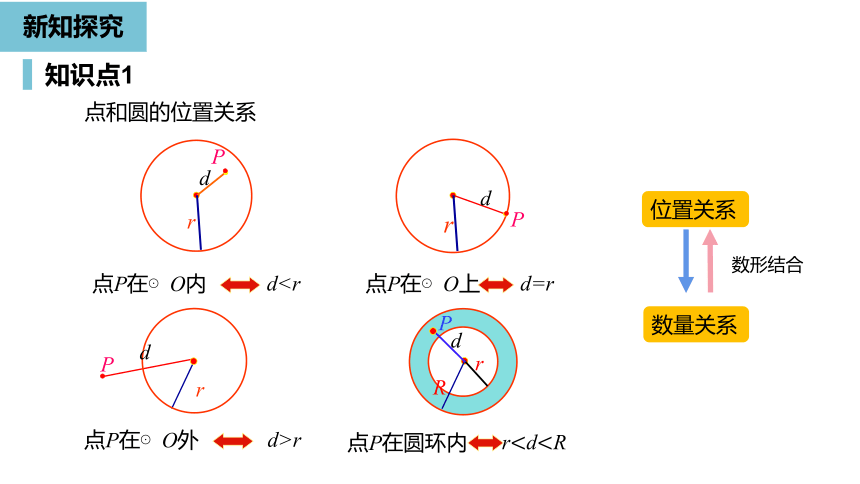
点和圆的位置关系
r
P
d
P
r
d
P
r
d
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r数形结合
位置关系
数量关系
R
r
P
d
知识点1
新知探究
1.判断点与圆的位置关系的实质是判断点到圆心的距离和半径的大小关系.
2.已知点到圆心的距离与半径的关系,可以确定该点与圆的位置关系,反过来,由点与圆的位置关系也可以确定该点到圆心的距离与半径的关系.
3.圆的外部可以看成到圆心的距离大于半径的点的集合;圆的内部可以看成到圆心的距离小于半径的点的集合.
跟踪训练
新知探究
如图,△ABC中,∠ACB=
90°,AC=2
cm,
BC=4
cm,CM是AB边上的中线.
(1)
若以C为圆心,
cm为半径画圆,则点A,B,M与⊙C的位置关系如何?
(2)
若以C为圆心作⊙C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求⊙C的半径
r
的取值范围.
解:(1)
因为CA=2
cm<
cm,所以点A在⊙C内.
因为BC=4
cm>
cm,所以点B在⊙C外.
由勾股定理,得AB==2
(cm)
,
所以
CM=AB=
cm,所以点M在⊙C上.
跟踪训练
新知探究
解:(2)当点B在圆上时,
r=4
cm,
当点A在圆上时,r=2
cm,
当点M在圆上时,
r=
cm,
故满足题意的
r
的取值范围是2
cm<
r
<4
cm.
如图,△ABC中,∠ACB=
90°,AC=2
cm,
BC=4
cm,CM是AB边上的中线.
(1)
若以C为圆心,
cm为半径画圆,则点A,B,M与⊙C的位置关系如何?
(2)
若以C为圆心作⊙C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求⊙C的半径
r
的取值范围.
⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8
cm、10
cm、12
cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
.
随堂练习
1
圆O内
圆O上
圆O外
随堂练习
2
画出由所有到已知点O的距离大于或等于2
cm,并且小于或等于3
cm的点组成的图形.
3
cm
2
cm
O
随堂练习
3
体育课上,小明和小丽的铅球成绩分别是6.4
m和5.1
m,他们投出的铅球分
别落在图中哪个区域内?
小明:④
小丽:③
课堂小结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d对接中考
1
圆心为O的两个同心圆,半径分别为1和2,若OP=,则点P在(
)
A.大圆内
B.小圆内
C.小圆外
D.大圆内,小圆外
o
D
对接中考
2
如图,已知矩形ABCD的边AB=3,AD=4.
(1)
以A为圆心,4为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
解:AD=4=
r,故D点在⊙A上,
AB=3<
r,
故B点在⊙A内,
AC==5>
r,故C点在⊙A外.
对接中考
2
(2)
若以A点为圆心作⊙A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3如图,已知矩形ABCD的边AB=3,AD=4.
24.2.1点和圆的位置关系
点和圆、直线和圆的位置关系
知识回顾
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
圆的集合定义
学习目标
1.理解并掌握点和圆的三种位置关系.
2.经历探索点与圆的三种位置关系,体会数学分类讨论思考问题的方法.
课堂导入
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.下图是射击靶的示意图,它是由许多同心圆(圆心相同、半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
知识点1
新知探究
观察下图中点和圆O的位置关系有哪几种?
.
o
.
C
.
.
.
B
.
.A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
知识点1
新知探究
设点到圆心的距离为d,圆的半径为r,量一量在点和圆有三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
o
o
o
知识点1
新知探究
点和圆的位置关系
r
P
d
P
r
d
P
r
d
点P在⊙O内
d
d=r
点P在⊙O外
d>r
点P在圆环内
r
位置关系
数量关系
R
r
P
d
知识点1
新知探究
1.判断点与圆的位置关系的实质是判断点到圆心的距离和半径的大小关系.
2.已知点到圆心的距离与半径的关系,可以确定该点与圆的位置关系,反过来,由点与圆的位置关系也可以确定该点到圆心的距离与半径的关系.
3.圆的外部可以看成到圆心的距离大于半径的点的集合;圆的内部可以看成到圆心的距离小于半径的点的集合.
跟踪训练
新知探究
如图,△ABC中,∠ACB=
90°,AC=2
cm,
BC=4
cm,CM是AB边上的中线.
(1)
若以C为圆心,
cm为半径画圆,则点A,B,M与⊙C的位置关系如何?
(2)
若以C为圆心作⊙C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求⊙C的半径
r
的取值范围.
解:(1)
因为CA=2
cm<
cm,所以点A在⊙C内.
因为BC=4
cm>
cm,所以点B在⊙C外.
由勾股定理,得AB==2
(cm)
,
所以
CM=AB=
cm,所以点M在⊙C上.
跟踪训练
新知探究
解:(2)当点B在圆上时,
r=4
cm,
当点A在圆上时,r=2
cm,
当点M在圆上时,
r=
cm,
故满足题意的
r
的取值范围是2
cm<
r
<4
cm.
如图,△ABC中,∠ACB=
90°,AC=2
cm,
BC=4
cm,CM是AB边上的中线.
(1)
若以C为圆心,
cm为半径画圆,则点A,B,M与⊙C的位置关系如何?
(2)
若以C为圆心作⊙C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求⊙C的半径
r
的取值范围.
⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8
cm、10
cm、12
cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
.
随堂练习
1
圆O内
圆O上
圆O外
随堂练习
2
画出由所有到已知点O的距离大于或等于2
cm,并且小于或等于3
cm的点组成的图形.
3
cm
2
cm
O
随堂练习
3
体育课上,小明和小丽的铅球成绩分别是6.4
m和5.1
m,他们投出的铅球分
别落在图中哪个区域内?
小明:④
小丽:③
课堂小结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
1
圆心为O的两个同心圆,半径分别为1和2,若OP=,则点P在(
)
A.大圆内
B.小圆内
C.小圆外
D.大圆内,小圆外
o
D
对接中考
2
如图,已知矩形ABCD的边AB=3,AD=4.
(1)
以A为圆心,4为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
解:AD=4=
r,故D点在⊙A上,
AB=3<
r,
故B点在⊙A内,
AC==5>
r,故C点在⊙A外.
对接中考
2
(2)
若以A点为圆心作⊙A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3
同课章节目录
