人教版九年级数学上册24.2.2 直线和圆的位置关系(1)课件(21张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.2.2 直线和圆的位置关系(1)课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 673.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
24.2.2
直线和圆的位置关系
点和圆、直线和圆的位置关系
知识回顾
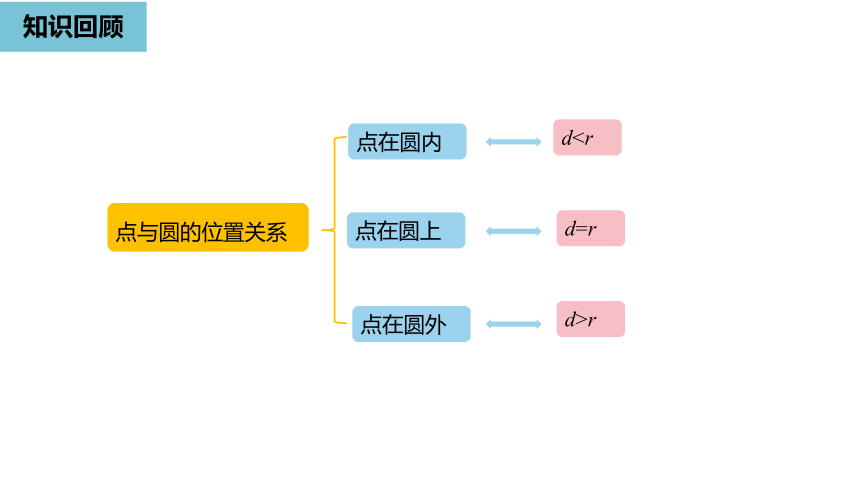
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d学习目标
1.了解直线和圆的位置关系.
3.理解直线和圆的三种位置关系时圆心到直线的距离d和圆的半径r之间的数量关系.
2.了解直线与圆的不同位置关系时的有关概念.
4.会运用直线和圆的三种位置关系的性质与判定进行有关计算.
课堂导入
如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
知识点1
新知探究
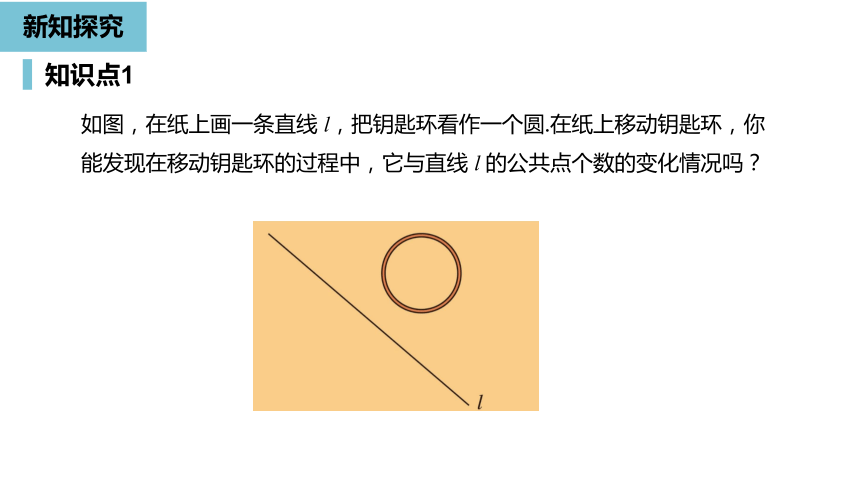
如图,在纸上画一条直线
l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线
l
的公共点个数的变化情况吗?
知识点1
新知探究
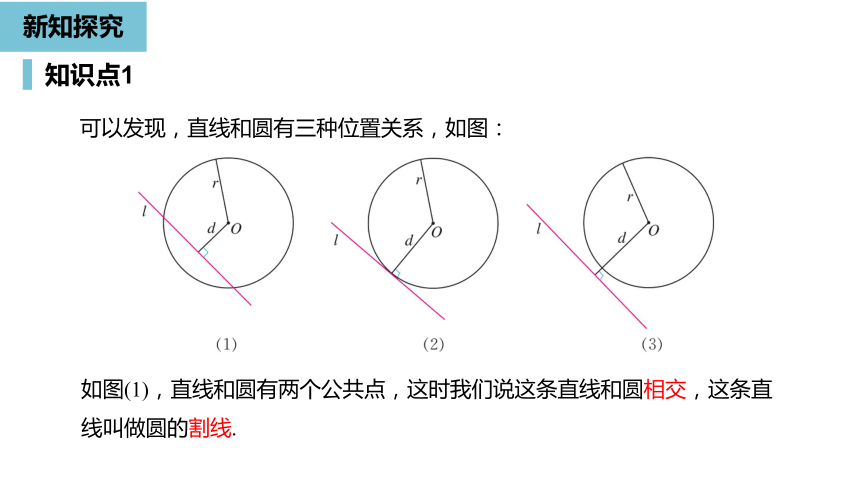
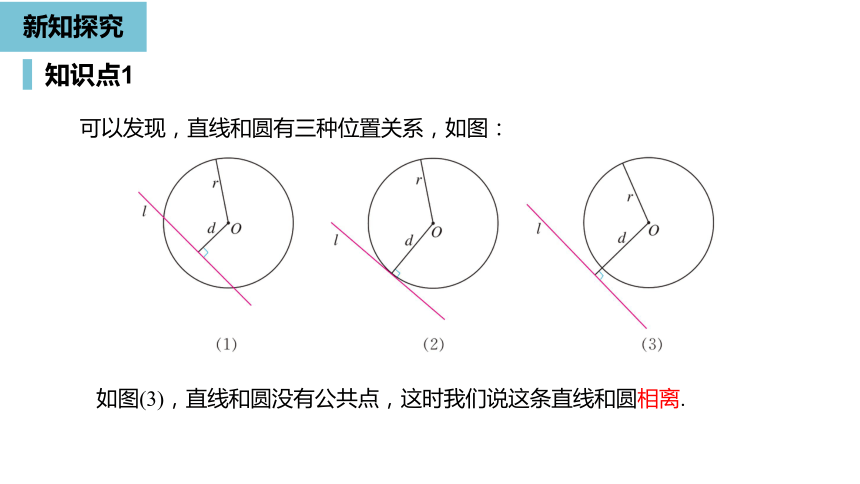
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
知识点1
新知探究
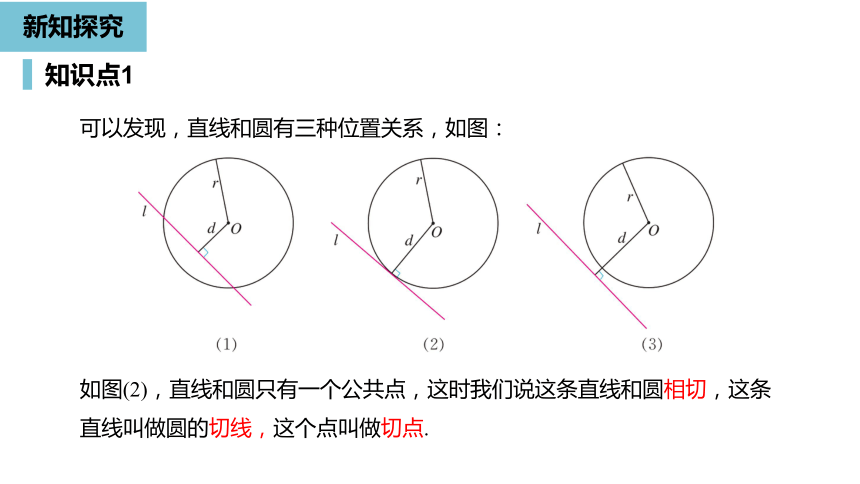
可以发现,直线和圆有三种位置关系,如图:
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
知识点1
新知探究
可以发现,直线和圆有三种位置关系,如图:
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
知识点1
新知探究
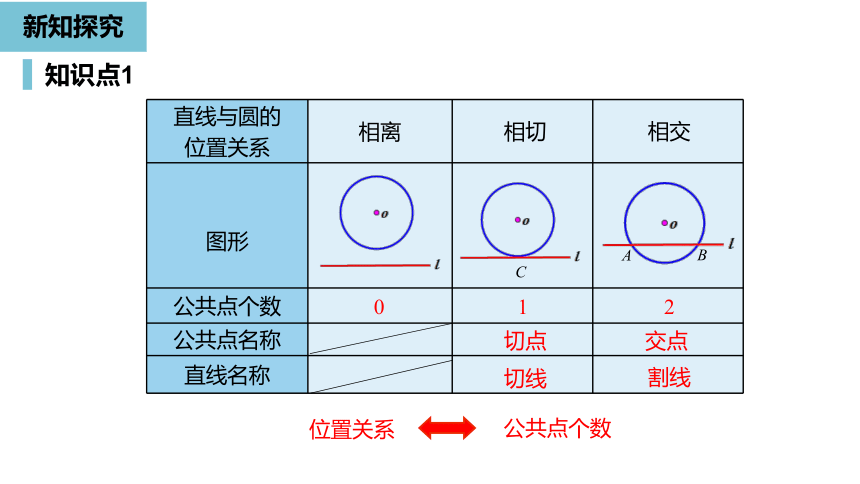
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2
交点
1
切点
切线
0
相离
相切
相交
位置关系
公共点个数
A
B
C
割线
知识点1
新知探究
同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
知识点1
新知探究
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
知识点1
新知探究
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
位置关系
数量关系
用圆心O到直线的距离d与圆的半径r的关系来区分直线与圆的位置关系:
∟
r
d
o
公共点个数
r
d
o
A
B
∟
r
d
o
C
知识点1
新知探究
1.判断直线和圆的位置关系有两种方法:
①将圆心到直线的距离与圆的半径相比较;
②根据直线与圆的交点的个数判定.
2.直线与圆相切是一种特殊的位置关系,此时直线与圆只有一个交点.
一个圆有无数条切线,每一条切线与圆都只有一个切点.
跟踪训练
新知探究
已知圆的直径为13
cm,设直线和圆心的距离为d.
(1)
若d
=4.5
cm,则直线与圆
,直线与圆有
个公共点;
(2)
若d
=6.5
cm,则直线与圆
,直线与圆有
个公共点;
(3)
若d
=
8
cm,则直线与圆
,直线与圆有
个公共点.
相交
2
相切
1
相离
0
随堂练习
1
已知⊙O的半径为5
cm,圆心O到直线
l
的距离为5cm,则直线
l
与⊙O的位置关系为(
)
B
A.相交
B.相切
C.相离
D.无法确定
随堂练习
2
如图,Rt△ABC中,∠C=90°,AC=3
cm,BC=4
cm,判断以点C为圆心,下列
r
为
半径的⊙C与AB的位置关系:
(1)
r
=2
cm;
(2)
r=2.4
cm;
(3)
r
=3
cm.
解:作CD⊥AB于D,如图,
∵∠C=90°,AC=3,BC=4,∴AB==5,
∵
BC?AC=CD?AB,∴CD=2.4,
(1)
当
r=2时,CD>r,所以⊙C与AB相离;
(2)
当
r=2.4时,CD=r,所以⊙C与AB相切;
(3)
当
r=3时,CD<r,所以⊙C与AB相交.
B
C
A
D
课堂小结
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:d>r
相切:d=r
相交:d0个:相离;1个:相切;2个:相交
d>r:相离
d=r:相切
d相离:0个
相切:1个
相交:2个
对接中考
1
如果直线上一点与一个圆的圆心的距离等于这个圆的半径,那么这条直线与这个圆的位置关系是(
)
C
A.相交
B.相切
C.相交或相切
D.以上都不正确
解:如果直线上一点与一个圆的圆心的距离等于这个圆的半径,
根据垂线段最短,则圆心到直线的距离小于或等于圆的半径,
从而直线和圆相交或相切.
对接中考
2
已知直线
y=
kx(k≠0)
经过点(12,
-5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)
,则m的取值范围为
.
解:把点(12,-5)代入直线
y=kx得,-5=12k,∴k=;
由
y=x平移m(m>0)个单位后得到的直线
l
所对应的函数关系式为y=
x+m(m>0),
对接中考
2
设直线
l
与
x
轴、y
轴分别交于点A,B,如图,
当x=0时,y=m;当y=0时,x=
m,∴A(m,0),B(0,m),
即OA=m,OB=m;在Rt△OAB中,AB==m,
过点O作OD⊥AB于D,∵S△ABO=OD?AB=OA?OB,∴OD×m=×m×m,
∵m>0,解得OD=
m,由直线与圆的位置关系可知m<6,解得0<m<.
如图,已知直线
y=
kx(k≠0)
经过点(12,
-5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)
,则m的取值范围为
.
O
A
B
x
y
l
D
0<m<
对接中考
3
某市计划在学校C的不远处修建一条东西方向的马路
,要求学校周围240
m的范围内不能有噪声.如图所示,学校北偏东45°的地方是一个勘测点A,北偏西60°的地方是另一个勘测点B,两个勘测点之间的距离为540m,为了使马路上行车的噪声不影响学校,沿AB方向修建马路是否符合要求?(参考数据:
≈1.7)
解:如图,过点C作CD⊥AB于点D.设CD=x
m.
因为∠ACD=45°,∠BCD=60°,所以AD=x
m,BC=2x
m,
所以BD=x
(m).
因为AB=540
m,所以
x+
x=540,所以
x
≈
200.
因为200<240,所以沿AB方向修建马路不符合要求.
D
24.2.2
直线和圆的位置关系
点和圆、直线和圆的位置关系
知识回顾
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
1.了解直线和圆的位置关系.
3.理解直线和圆的三种位置关系时圆心到直线的距离d和圆的半径r之间的数量关系.
2.了解直线与圆的不同位置关系时的有关概念.
4.会运用直线和圆的三种位置关系的性质与判定进行有关计算.
课堂导入
如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
知识点1
新知探究
如图,在纸上画一条直线
l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线
l
的公共点个数的变化情况吗?
知识点1
新知探究
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
知识点1
新知探究
可以发现,直线和圆有三种位置关系,如图:
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
知识点1
新知探究
可以发现,直线和圆有三种位置关系,如图:
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
知识点1
新知探究
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2
交点
1
切点
切线
0
相离
相切
相交
位置关系
公共点个数
A
B
C
割线
知识点1
新知探究
同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
知识点1
新知探究
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
知识点1
新知探究
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
位置关系
数量关系
用圆心O到直线的距离d与圆的半径r的关系来区分直线与圆的位置关系:
∟
r
d
o
公共点个数
r
d
o
A
B
∟
r
d
o
C
知识点1
新知探究
1.判断直线和圆的位置关系有两种方法:
①将圆心到直线的距离与圆的半径相比较;
②根据直线与圆的交点的个数判定.
2.直线与圆相切是一种特殊的位置关系,此时直线与圆只有一个交点.
一个圆有无数条切线,每一条切线与圆都只有一个切点.
跟踪训练
新知探究
已知圆的直径为13
cm,设直线和圆心的距离为d.
(1)
若d
=4.5
cm,则直线与圆
,直线与圆有
个公共点;
(2)
若d
=6.5
cm,则直线与圆
,直线与圆有
个公共点;
(3)
若d
=
8
cm,则直线与圆
,直线与圆有
个公共点.
相交
2
相切
1
相离
0
随堂练习
1
已知⊙O的半径为5
cm,圆心O到直线
l
的距离为5cm,则直线
l
与⊙O的位置关系为(
)
B
A.相交
B.相切
C.相离
D.无法确定
随堂练习
2
如图,Rt△ABC中,∠C=90°,AC=3
cm,BC=4
cm,判断以点C为圆心,下列
r
为
半径的⊙C与AB的位置关系:
(1)
r
=2
cm;
(2)
r=2.4
cm;
(3)
r
=3
cm.
解:作CD⊥AB于D,如图,
∵∠C=90°,AC=3,BC=4,∴AB==5,
∵
BC?AC=CD?AB,∴CD=2.4,
(1)
当
r=2时,CD>r,所以⊙C与AB相离;
(2)
当
r=2.4时,CD=r,所以⊙C与AB相切;
(3)
当
r=3时,CD<r,所以⊙C与AB相交.
B
C
A
D
课堂小结
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:d>r
相切:d=r
相交:d
d>r:相离
d=r:相切
d
相切:1个
相交:2个
对接中考
1
如果直线上一点与一个圆的圆心的距离等于这个圆的半径,那么这条直线与这个圆的位置关系是(
)
C
A.相交
B.相切
C.相交或相切
D.以上都不正确
解:如果直线上一点与一个圆的圆心的距离等于这个圆的半径,
根据垂线段最短,则圆心到直线的距离小于或等于圆的半径,
从而直线和圆相交或相切.
对接中考
2
已知直线
y=
kx(k≠0)
经过点(12,
-5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)
,则m的取值范围为
.
解:把点(12,-5)代入直线
y=kx得,-5=12k,∴k=;
由
y=x平移m(m>0)个单位后得到的直线
l
所对应的函数关系式为y=
x+m(m>0),
对接中考
2
设直线
l
与
x
轴、y
轴分别交于点A,B,如图,
当x=0时,y=m;当y=0时,x=
m,∴A(m,0),B(0,m),
即OA=m,OB=m;在Rt△OAB中,AB==m,
过点O作OD⊥AB于D,∵S△ABO=OD?AB=OA?OB,∴OD×m=×m×m,
∵m>0,解得OD=
m,由直线与圆的位置关系可知m<6,解得0<m<.
如图,已知直线
y=
kx(k≠0)
经过点(12,
-5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)
,则m的取值范围为
.
O
A
B
x
y
l
D
0<m<
对接中考
3
某市计划在学校C的不远处修建一条东西方向的马路
,要求学校周围240
m的范围内不能有噪声.如图所示,学校北偏东45°的地方是一个勘测点A,北偏西60°的地方是另一个勘测点B,两个勘测点之间的距离为540m,为了使马路上行车的噪声不影响学校,沿AB方向修建马路是否符合要求?(参考数据:
≈1.7)
解:如图,过点C作CD⊥AB于点D.设CD=x
m.
因为∠ACD=45°,∠BCD=60°,所以AD=x
m,BC=2x
m,
所以BD=x
(m).
因为AB=540
m,所以
x+
x=540,所以
x
≈
200.
因为200<240,所以沿AB方向修建马路不符合要求.
D
同课章节目录
