人教版九年级数学上册24.4弧长和扇形面积(2)课件(20张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.4弧长和扇形面积(2)课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 20.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 20:25:12 | ||
图片预览




文档简介
(共20张PPT)
24.4
第2课时
弧长和扇形面积
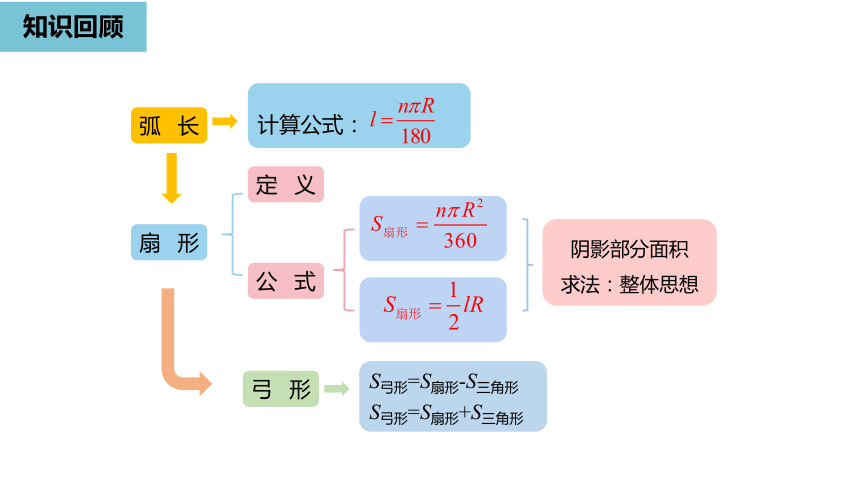
知识回顾
弧长
计算公式:
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
学习目标
2.会求圆锥的侧面积,并能解决一些简单的实际问题.
1.体会圆锥侧面积的探索过程.
课堂导入
圆锥是由一个底面和一个侧面围成的几何体.
课堂导入
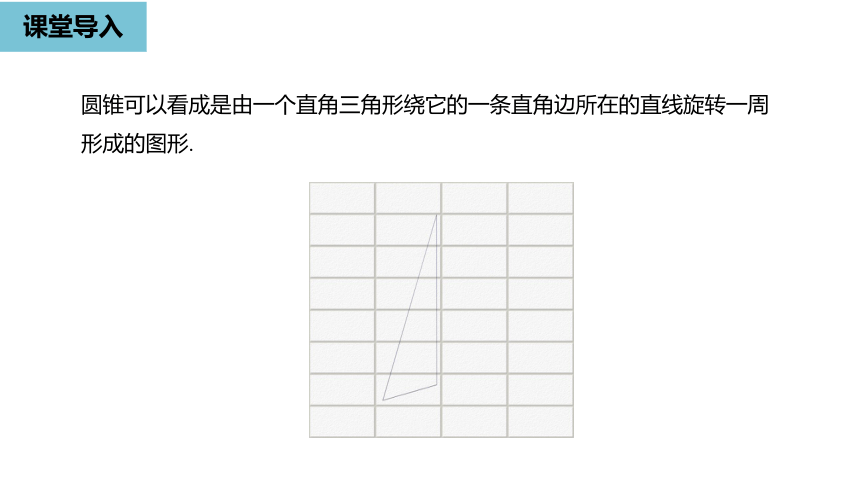
圆锥可以看成是由一个直角三角形绕它的一条直角边所在的直线旋转一周形成的图形.
知识点1
新知探究
圆锥的高
母线
S
A
O
B
我们把连接圆锥的顶点S和底面圆上任一点的连线叫做圆锥的母线.
圆锥有无数条母线,它们都相等.
连接圆锥的顶点与底面圆心的线段叫做圆锥的高.
知识点1
新知探究
h
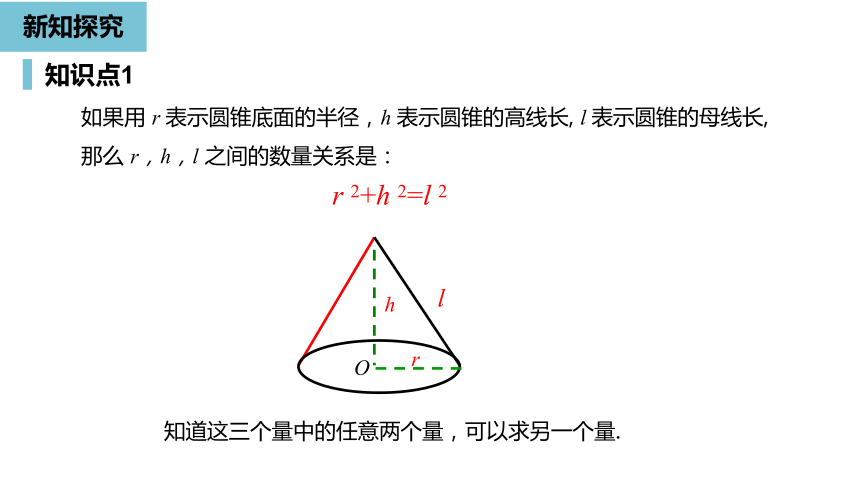
如果用
r
表示圆锥底面的半径,h
表示圆锥的高线长,
l
表示圆锥的母线长,那么
r,h,l
之间的数量关系是:
r
2+h
2=l
2
O
r
知道这三个量中的任意两个量,可以求另一个量.
知识点1
新知探究
l
o
r
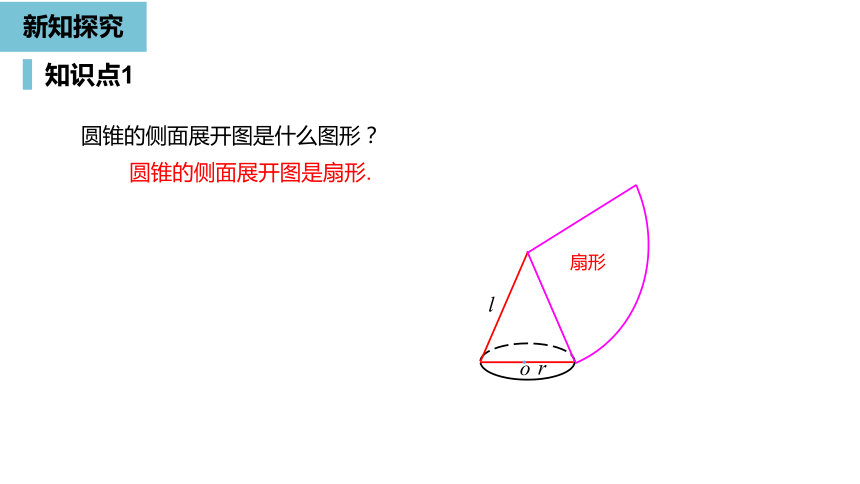
圆锥的侧面展开图是什么图形?
扇形
圆锥的侧面展开图是扇形.
知识点1
新知探究
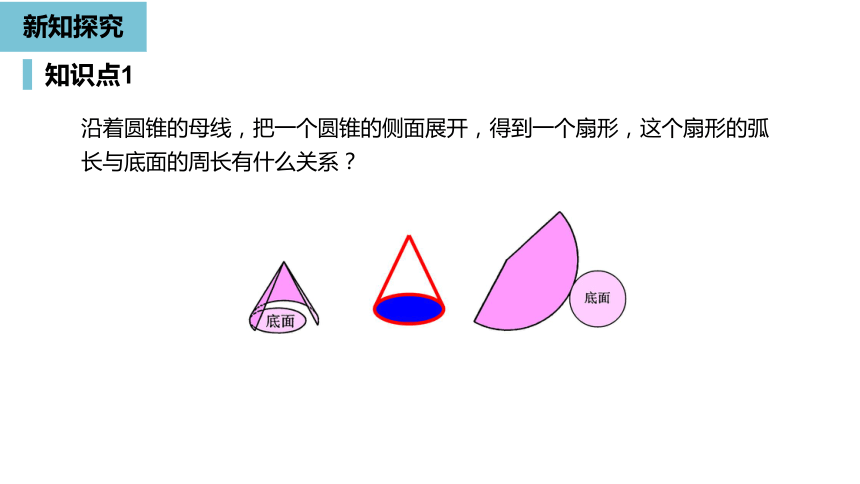
沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
知识点1
新知探究
圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?
知识点1
新知探究
r
扇形
其侧面展开图扇形的半径
=
母线的长
l
.
侧面展开图扇形的弧长
=
底面周长2πr
.
知识点1
新知探究
如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.设圆锥的母线长为
l
,底面圆的半径为
r
,那么这个扇形的半径为
l
,扇形的弧长为
2πr,因此圆锥的侧面积S侧=S扇形=×2πr×l=πrl,圆锥的全面积S全
=S侧+S底
=
πrl+πr2=πr(
l+
r).
圆锥侧面展开图的半径是圆锥的母线长,要与底面半径区别开来.
知识点1
新知探究
例
蒙古包可以近似地看作由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为35
m2,高为3.5
m,外围高为1.5
m的蒙古包,至少需要多少平方米的毛毡(精确到1m2)?
解:如图是一个蒙古包示意图.
根据题意,下部圆柱的底面积为35m2,高为1.5m;上部圆锥的高为3.5-1.5=2(m).
圆柱的底面半径为
侧面积为2π×3.34×1.5≈31.46(m2).
知识点1
新知探究
圆锥的母线长为
侧面展开扇形的弧长为
圆锥的侧面积为
20×(31.46+40.81)≈1446(m2).
跟踪训练
新知探究
一个圆锥的母线长是9,底面圆的半径是6,则这个圆锥的侧面积是(
)
C
A.81π
B.27π
C.54π
D.18π
解:这个圆锥的侧面积=×9×2π×6=54π.
随堂练习
1
用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面圆半径是(
)
A
A.10
B.20
C.10π
D.20π
解:设该圆锥底面圆的半径为
r,
根据题意得2πr
=
,解得
r=10,
即该圆锥底面圆的半径为10.
随堂练习
2
圆锥的底面圆直径是80
cm,母线长是90cm.求它的侧面展开图的圆心角和圆锥的全面积.
解:设母线长为R,圆锥底面周长为C,
则
C=πd=π×80=80π
(cm),
又C=
,则n=
=160,
圆锥侧面积==
=3600π(cm?),
圆锥底面积=πr?=1600π(cm?),
圆锥的全面积=3600π+1600π=5200π(cm?).
课堂小结
r2+h2=l2
S圆锥侧=πrl
S
圆锥全=
S圆锥侧+
S圆锥底=
πrl+πr2
①其侧面展开图扇形的半径=母线的长l
②侧面展开图扇形的弧长=底面周长
重要图形
重要结论
圆锥的高
母线
S
A
O
B
r
h
o
r
l
侧面
展开图
底面
对接中考
1
如图(1),如果从半径为5
cm的圆形纸片上剪去
圆周的一个扇形,将留下的扇形围成一个圆锥的侧面(接缝处不重叠,如图(2)所示)
,那么这个圆锥的高是
cm.
3
解:∵从半径为5cm的圆形纸片上剪去圆周的一个扇形,
∴留下的扇形的弧长=
=8π
cm,
根据底面圆的周长等于扇形弧长,
得圆锥的底面半径r=
=4
cm,
圆锥的高为
=3
cm
.
解:由题意知,圆锥底面圆的直径BC=6
m,
故圆锥底面圆的周长为6π
m.
设圆锥侧面展开后的扇形的圆心角为
n°,
则6π=
,解得n=180,所以展开后∠BAP=90°,
所以圆锥的侧面展开图如图所示.又AP=
AC=3
m,
所以在Rt?ABP中,
BP=(m),
所以小猫所经过的最短路程为m.
对接中考
2
如图所示,有一个圆锥形的粮堆,其轴截面是边长为6
m的等边三角形,在圆锥的母线AC的中点P处有一只老鼠正在偷吃粮食,此时小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠.求小猫所经过的最短路程.
24.4
第2课时
弧长和扇形面积
知识回顾
弧长
计算公式:
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
学习目标
2.会求圆锥的侧面积,并能解决一些简单的实际问题.
1.体会圆锥侧面积的探索过程.
课堂导入
圆锥是由一个底面和一个侧面围成的几何体.
课堂导入
圆锥可以看成是由一个直角三角形绕它的一条直角边所在的直线旋转一周形成的图形.
知识点1
新知探究
圆锥的高
母线
S
A
O
B
我们把连接圆锥的顶点S和底面圆上任一点的连线叫做圆锥的母线.
圆锥有无数条母线,它们都相等.
连接圆锥的顶点与底面圆心的线段叫做圆锥的高.
知识点1
新知探究
h
如果用
r
表示圆锥底面的半径,h
表示圆锥的高线长,
l
表示圆锥的母线长,那么
r,h,l
之间的数量关系是:
r
2+h
2=l
2
O
r
知道这三个量中的任意两个量,可以求另一个量.
知识点1
新知探究
l
o
r
圆锥的侧面展开图是什么图形?
扇形
圆锥的侧面展开图是扇形.
知识点1
新知探究
沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
知识点1
新知探究
圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?
知识点1
新知探究
r
扇形
其侧面展开图扇形的半径
=
母线的长
l
.
侧面展开图扇形的弧长
=
底面周长2πr
.
知识点1
新知探究
如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.设圆锥的母线长为
l
,底面圆的半径为
r
,那么这个扇形的半径为
l
,扇形的弧长为
2πr,因此圆锥的侧面积S侧=S扇形=×2πr×l=πrl,圆锥的全面积S全
=S侧+S底
=
πrl+πr2=πr(
l+
r).
圆锥侧面展开图的半径是圆锥的母线长,要与底面半径区别开来.
知识点1
新知探究
例
蒙古包可以近似地看作由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为35
m2,高为3.5
m,外围高为1.5
m的蒙古包,至少需要多少平方米的毛毡(精确到1m2)?
解:如图是一个蒙古包示意图.
根据题意,下部圆柱的底面积为35m2,高为1.5m;上部圆锥的高为3.5-1.5=2(m).
圆柱的底面半径为
侧面积为2π×3.34×1.5≈31.46(m2).
知识点1
新知探究
圆锥的母线长为
侧面展开扇形的弧长为
圆锥的侧面积为
20×(31.46+40.81)≈1446(m2).
跟踪训练
新知探究
一个圆锥的母线长是9,底面圆的半径是6,则这个圆锥的侧面积是(
)
C
A.81π
B.27π
C.54π
D.18π
解:这个圆锥的侧面积=×9×2π×6=54π.
随堂练习
1
用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面圆半径是(
)
A
A.10
B.20
C.10π
D.20π
解:设该圆锥底面圆的半径为
r,
根据题意得2πr
=
,解得
r=10,
即该圆锥底面圆的半径为10.
随堂练习
2
圆锥的底面圆直径是80
cm,母线长是90cm.求它的侧面展开图的圆心角和圆锥的全面积.
解:设母线长为R,圆锥底面周长为C,
则
C=πd=π×80=80π
(cm),
又C=
,则n=
=160,
圆锥侧面积==
=3600π(cm?),
圆锥底面积=πr?=1600π(cm?),
圆锥的全面积=3600π+1600π=5200π(cm?).
课堂小结
r2+h2=l2
S圆锥侧=πrl
S
圆锥全=
S圆锥侧+
S圆锥底=
πrl+πr2
①其侧面展开图扇形的半径=母线的长l
②侧面展开图扇形的弧长=底面周长
重要图形
重要结论
圆锥的高
母线
S
A
O
B
r
h
o
r
l
侧面
展开图
底面
对接中考
1
如图(1),如果从半径为5
cm的圆形纸片上剪去
圆周的一个扇形,将留下的扇形围成一个圆锥的侧面(接缝处不重叠,如图(2)所示)
,那么这个圆锥的高是
cm.
3
解:∵从半径为5cm的圆形纸片上剪去圆周的一个扇形,
∴留下的扇形的弧长=
=8π
cm,
根据底面圆的周长等于扇形弧长,
得圆锥的底面半径r=
=4
cm,
圆锥的高为
=3
cm
.
解:由题意知,圆锥底面圆的直径BC=6
m,
故圆锥底面圆的周长为6π
m.
设圆锥侧面展开后的扇形的圆心角为
n°,
则6π=
,解得n=180,所以展开后∠BAP=90°,
所以圆锥的侧面展开图如图所示.又AP=
AC=3
m,
所以在Rt?ABP中,
BP=(m),
所以小猫所经过的最短路程为m.
对接中考
2
如图所示,有一个圆锥形的粮堆,其轴截面是边长为6
m的等边三角形,在圆锥的母线AC的中点P处有一只老鼠正在偷吃粮食,此时小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠.求小猫所经过的最短路程.
同课章节目录
