人教版九年级数学上册25.3用频率估计概率(2)课件(26张PPT)
文档属性
| 名称 | 人教版九年级数学上册25.3用频率估计概率(2)课件(26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 601.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 20:42:06 | ||
图片预览






文档简介
(共26张PPT)
25.3
第2课时
用频率估计概率
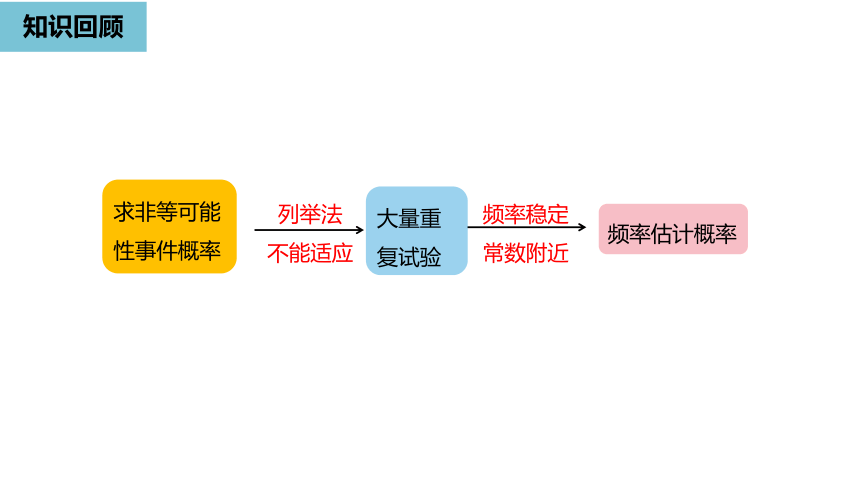
知识回顾
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
学习目标
1.结合具体情境掌握如何用频率估计概率.
2.通过概率计算进一步比较概率与频率之间的关系.
课堂导入
上节课我们学习了用频率估计概率,其在实际生活中有哪些应用呢?能够解决哪些实际问题呢?本节课我们将解决这些问题.
知识点1
新知探究
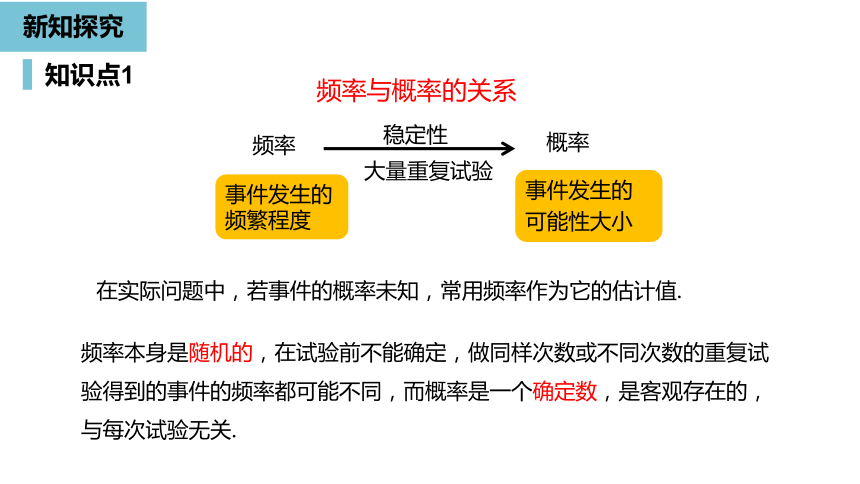
频率与概率的关系
频率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
概率
知识点1
新知探究
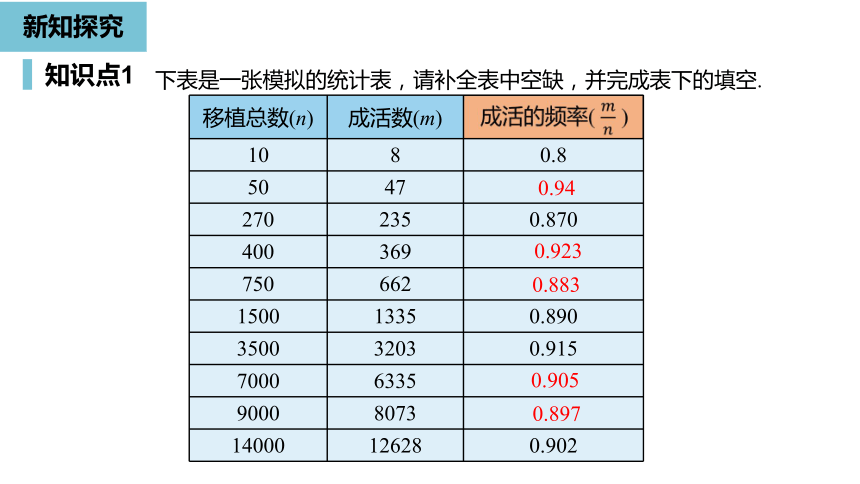
某林业部门要考察某种幼树在一定条件下的移植成活率,应采用什么具体做法?
幼树移植成活率是实际问题中的一种概率.这个问题中幼树移植“成活”与“不成活”两种结果可能性是否相等未知,所以成活率要由频率去估计.
在同样条件下,对这种幼树进行大量移植,并统计成活情况,计算成活率的估计值.
知识点1
新知探究
移植总数(n)
成活数(m)
10
8
0.8
50
47
270
235
0.870
400
369
750
662
1500
1335
0.890
3500
3203
0.915
7000
6335
9000
8073
14000
12628
0.902
0.94
0.923
0.883
0.905
0.897
下表是一张模拟的统计表,请补全表中空缺,并完成表下的填空.
知识点1
新知探究
由上表可以发现,幼树移植成活的频率在0.9左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为0.9.
知识点1
新知探究
某水果公司以2元/千克的成本新进了10
000千克柑橘,如果公司希望这些柑橘能够获得利润5
000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.请你帮忙完成此表.
知识点1
新知探究
柑橘总质量(n)/千克
损坏柑橘质量(m)/千克
50
5.50
0.110
100
10.5
0.105
150
15.15
200
19.42
250
24.25
300
30.93
350
35.32
400
39.24
450
44.57
500
51.54
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
知识点1
新知探究
填完表后,从表中可以看出,随着柑橘质量的增加,柑橘损坏的频率越来越稳定.柑橘总质量为500
kg时的损坏频率为0.103,于是可以估计柑橘损坏的概率为0.1
(结果保留小数点后一位).由此可知,柑橘完好的概率为0.9.
知识点1
新知探究
解:根据估计的概率可以知道,在10
000千克柑橘中完好柑橘的质量为10
000×0.9=9
000(千克),
完好柑橘的实际成本为
(元/千克)
设每千克柑橘的销价为x元,则应有(x-2.22)×9
000=5
000,
解得
x≈2.8.
因此,出售柑橘时每千克大约定价为2.8元可获利润5
000元.
跟踪训练
新知探究
一粒木质中国象棋“兵”,它的正面雕刻一个“兵”字,它的反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某试验小组做了棋子下掷的试验,试验数据如下表:
(1)
请将数据表补充完整;
实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上的次数
14
38
47
52
66
78
88
“兵”字面朝上的频率
0.70
0.45
0.63
0.59
0.55
0.56
18
0.52
0.55
跟踪训练
新知探究
(2)
在下图中画出“兵”字面朝上的频率分布折线图;
实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上的次数
14
18
38
47
52
66
78
88
“兵”字面朝上的频率
0.70
0.45
0.63
0.59
0.52
0.55
0.56
0.55
跟踪训练
新知探究
(3)如果试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少(结果保留小数点后两位).
解:随着试验次数的增加,“兵”字面朝上的频率稳定在0.55附近,
所以估计“兵”字面朝上的概率是0.55.
实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上的次数
14
18
38
47
52
66
78
88
“兵”字面朝上的频率
0.70
0.45
0.63
0.59
0.52
0.55
0.56
0.55
随堂练习
1
黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客,某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.
7,该果农今年的蓝莓总产量约为800
kg,由此估计该果农今年的“优质蓝莓”产量约是
kg.
560
解:由题意可得该果农今年的“优质蓝莓”产量约是
800×0.7=560(kg).
随堂练习
2
下表记录了某种幼树在一定条件下移植成活情况.
0.9
移植总数n
400
1
500
3
500
7
000
9
000
14
000
成活数m
325
1
336
3
203
6
335
8
073
12
628
0.813
0.891
0.915
0.905
0.897
0.902
由此估计这种幼树在此条件下移植成活的概率约是
.
(精确到0.1).
随堂练习
3
一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%
,那么可以推算出n大约是(
)
D
A.6
B.10
C.18
D.20
解:根据题意得
=30%,解得
n=20.
课堂小结
用频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概
率但概率与频率无关
对接中考
1
我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计.用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部,如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为
.
(用含m,n的式子表示)
对接中考
1
解:随机产生m个有序数对(x,y),对应的点在平面直角坐标系中全部在如图所示的正方形的边界及其内部,
这些点中到原点的距离小于或等于1的n个点在图中阴影部分内,
则有
,
∴π=
.
对接中考
2
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
(1)
上述试验中“4朝下”的频率是
;
朝下数字
1
2
3
4
出现的次数
16
20
14
10
对接中考
2
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
(2)“根据试验结果,投掷一次正四面体,出现2朝下的概率是
”的说法正确吗?为什么?
朝下数字
1
2
3
4
出现的次数
16
20
14
10
解:(2)
这种说法是错误的.在60次试验中,“2朝下”的频率为
并不能说明“2朝下”这一事件发生的概率为
.只有当试验的总次数很大时,事件发生的频率才会稳定在相应的事件发生的概率附近.
对接中考
2
(3)
随机投掷正四面体两次,请用列表法求两次朝下的数字之和大于4的概率.
解:随机投掷正四面体两次,所有可能出现的结果如下:
由表格可知,共有16种结果,且每种结果出现的可能性相等,
其中两次朝下的数字之和大于4的结果有10种.
故P(两次朝下的数字之和大于4)
=
.
对接中考
3
某地区林业局要考察种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
0.9
0.9
(1)
这种树苗成活的频率稳定在
,成活的概率估计值为
;
(结果保留小数点后1位)
对接中考
3
(2)
该地区已经移植这种树苗5万棵.
①
估计这种树苗成活
万棵;
②
如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
4.5
解:设还需移植这种树苗x万棵.
根据题意,得(x+5)×0.9=18,解得x=15.
答:该地区还需移植这种树苗约15万棵.
25.3
第2课时
用频率估计概率
知识回顾
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
学习目标
1.结合具体情境掌握如何用频率估计概率.
2.通过概率计算进一步比较概率与频率之间的关系.
课堂导入
上节课我们学习了用频率估计概率,其在实际生活中有哪些应用呢?能够解决哪些实际问题呢?本节课我们将解决这些问题.
知识点1
新知探究
频率与概率的关系
频率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
概率
知识点1
新知探究
某林业部门要考察某种幼树在一定条件下的移植成活率,应采用什么具体做法?
幼树移植成活率是实际问题中的一种概率.这个问题中幼树移植“成活”与“不成活”两种结果可能性是否相等未知,所以成活率要由频率去估计.
在同样条件下,对这种幼树进行大量移植,并统计成活情况,计算成活率的估计值.
知识点1
新知探究
移植总数(n)
成活数(m)
10
8
0.8
50
47
270
235
0.870
400
369
750
662
1500
1335
0.890
3500
3203
0.915
7000
6335
9000
8073
14000
12628
0.902
0.94
0.923
0.883
0.905
0.897
下表是一张模拟的统计表,请补全表中空缺,并完成表下的填空.
知识点1
新知探究
由上表可以发现,幼树移植成活的频率在0.9左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为0.9.
知识点1
新知探究
某水果公司以2元/千克的成本新进了10
000千克柑橘,如果公司希望这些柑橘能够获得利润5
000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.请你帮忙完成此表.
知识点1
新知探究
柑橘总质量(n)/千克
损坏柑橘质量(m)/千克
50
5.50
0.110
100
10.5
0.105
150
15.15
200
19.42
250
24.25
300
30.93
350
35.32
400
39.24
450
44.57
500
51.54
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
知识点1
新知探究
填完表后,从表中可以看出,随着柑橘质量的增加,柑橘损坏的频率越来越稳定.柑橘总质量为500
kg时的损坏频率为0.103,于是可以估计柑橘损坏的概率为0.1
(结果保留小数点后一位).由此可知,柑橘完好的概率为0.9.
知识点1
新知探究
解:根据估计的概率可以知道,在10
000千克柑橘中完好柑橘的质量为10
000×0.9=9
000(千克),
完好柑橘的实际成本为
(元/千克)
设每千克柑橘的销价为x元,则应有(x-2.22)×9
000=5
000,
解得
x≈2.8.
因此,出售柑橘时每千克大约定价为2.8元可获利润5
000元.
跟踪训练
新知探究
一粒木质中国象棋“兵”,它的正面雕刻一个“兵”字,它的反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某试验小组做了棋子下掷的试验,试验数据如下表:
(1)
请将数据表补充完整;
实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上的次数
14
38
47
52
66
78
88
“兵”字面朝上的频率
0.70
0.45
0.63
0.59
0.55
0.56
18
0.52
0.55
跟踪训练
新知探究
(2)
在下图中画出“兵”字面朝上的频率分布折线图;
实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上的次数
14
18
38
47
52
66
78
88
“兵”字面朝上的频率
0.70
0.45
0.63
0.59
0.52
0.55
0.56
0.55
跟踪训练
新知探究
(3)如果试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少(结果保留小数点后两位).
解:随着试验次数的增加,“兵”字面朝上的频率稳定在0.55附近,
所以估计“兵”字面朝上的概率是0.55.
实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上的次数
14
18
38
47
52
66
78
88
“兵”字面朝上的频率
0.70
0.45
0.63
0.59
0.52
0.55
0.56
0.55
随堂练习
1
黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客,某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.
7,该果农今年的蓝莓总产量约为800
kg,由此估计该果农今年的“优质蓝莓”产量约是
kg.
560
解:由题意可得该果农今年的“优质蓝莓”产量约是
800×0.7=560(kg).
随堂练习
2
下表记录了某种幼树在一定条件下移植成活情况.
0.9
移植总数n
400
1
500
3
500
7
000
9
000
14
000
成活数m
325
1
336
3
203
6
335
8
073
12
628
0.813
0.891
0.915
0.905
0.897
0.902
由此估计这种幼树在此条件下移植成活的概率约是
.
(精确到0.1).
随堂练习
3
一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%
,那么可以推算出n大约是(
)
D
A.6
B.10
C.18
D.20
解:根据题意得
=30%,解得
n=20.
课堂小结
用频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概
率但概率与频率无关
对接中考
1
我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计.用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部,如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为
.
(用含m,n的式子表示)
对接中考
1
解:随机产生m个有序数对(x,y),对应的点在平面直角坐标系中全部在如图所示的正方形的边界及其内部,
这些点中到原点的距离小于或等于1的n个点在图中阴影部分内,
则有
,
∴π=
.
对接中考
2
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
(1)
上述试验中“4朝下”的频率是
;
朝下数字
1
2
3
4
出现的次数
16
20
14
10
对接中考
2
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
(2)“根据试验结果,投掷一次正四面体,出现2朝下的概率是
”的说法正确吗?为什么?
朝下数字
1
2
3
4
出现的次数
16
20
14
10
解:(2)
这种说法是错误的.在60次试验中,“2朝下”的频率为
并不能说明“2朝下”这一事件发生的概率为
.只有当试验的总次数很大时,事件发生的频率才会稳定在相应的事件发生的概率附近.
对接中考
2
(3)
随机投掷正四面体两次,请用列表法求两次朝下的数字之和大于4的概率.
解:随机投掷正四面体两次,所有可能出现的结果如下:
由表格可知,共有16种结果,且每种结果出现的可能性相等,
其中两次朝下的数字之和大于4的结果有10种.
故P(两次朝下的数字之和大于4)
=
.
对接中考
3
某地区林业局要考察种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
0.9
0.9
(1)
这种树苗成活的频率稳定在
,成活的概率估计值为
;
(结果保留小数点后1位)
对接中考
3
(2)
该地区已经移植这种树苗5万棵.
①
估计这种树苗成活
万棵;
②
如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
4.5
解:设还需移植这种树苗x万棵.
根据题意,得(x+5)×0.9=18,解得x=15.
答:该地区还需移植这种树苗约15万棵.
同课章节目录
