人教版九年级数学上册25章概率初步小结(2)课件(20张PPT)
文档属性
| 名称 | 人教版九年级数学上册25章概率初步小结(2)课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 402.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-31 20:43:34 | ||
图片预览




文档简介
(共20张PPT)
第2课时
25章概率初步小结
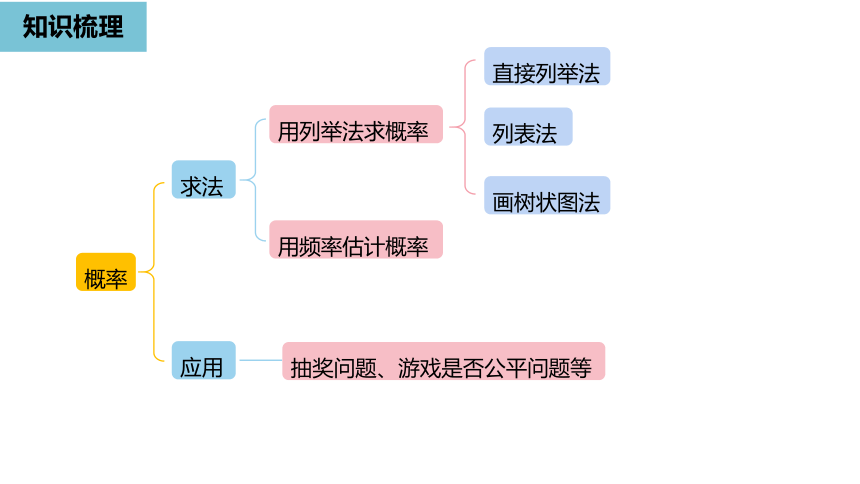
知识梳理
概率
求法
应用
直接列举法
列表法
画树状图法
用列举法求概率
用频率估计概率
抽奖问题、游戏是否公平问题等
知识梳理
直接列举法
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,那么出现每一种结果的概率都是
.
如果事件A包括其中的m种可能的结果,那么事件A发生的概率
P(A)
.
m个
(1)
直接列举试验结果时,要有一定的顺序性,保证结果不重不漏.
(2)
用列举法求概率的前提有两个:
①所有可能出现的结果是有限个;②每个结果出现的可能性相等.
知识梳理
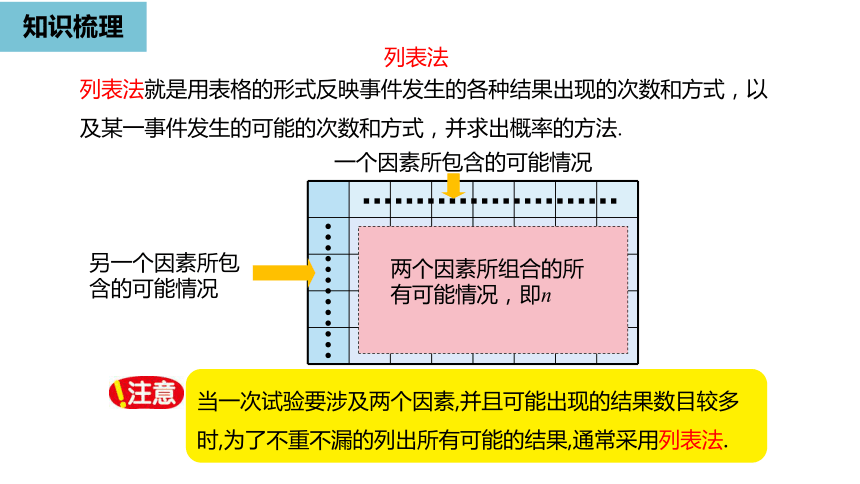
列表法
列表法就是用表格的形式反映事件发生的各种结果出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法.
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
知识梳理
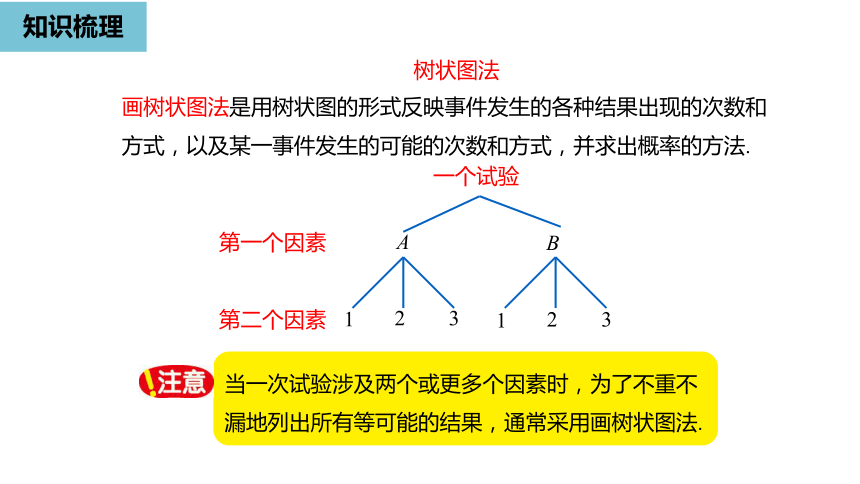
树状图法
画树状图法是用树状图的形式反映事件发生的各种结果出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法.
一个试验
第一个因素
第二个因素
A
B
1
2
3
1
2
3
当一次试验涉及两个或更多个因素时,为了不重不漏地列出所有等可能的结果,通常采用画树状图法.
知识梳理
用频率估计概率
从长期实践中,人们观察到对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件发生的频率,总在一个固定数的附近摆动,显示出一定的稳定性.因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
用频率估计概率时,必须做足够多的试验才能使频率趋于稳定,并且每次试验必须在相同条件下进行,试验次数越多,得到的频率值就越接近概率,规律就越明显,此时可以用频率的稳定值估计事件发生的概率.
知识梳理
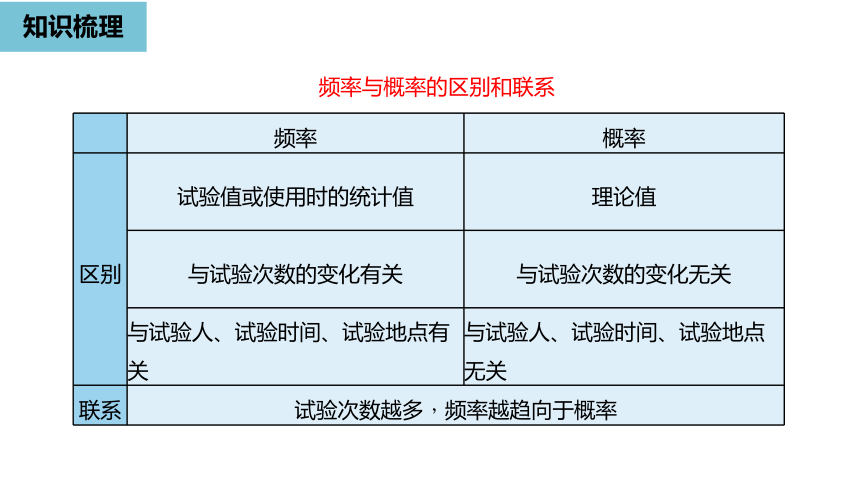
频率
概率
区别
试验值或使用时的统计值
理论值
与试验次数的变化有关
与试验次数的变化无关
与试验人、试验时间、试验地点有关
与试验人、试验时间、试验地点无关
联系
试验次数越多,频率越趋向于概率
频率与概率的区别和联系
重点解析
1
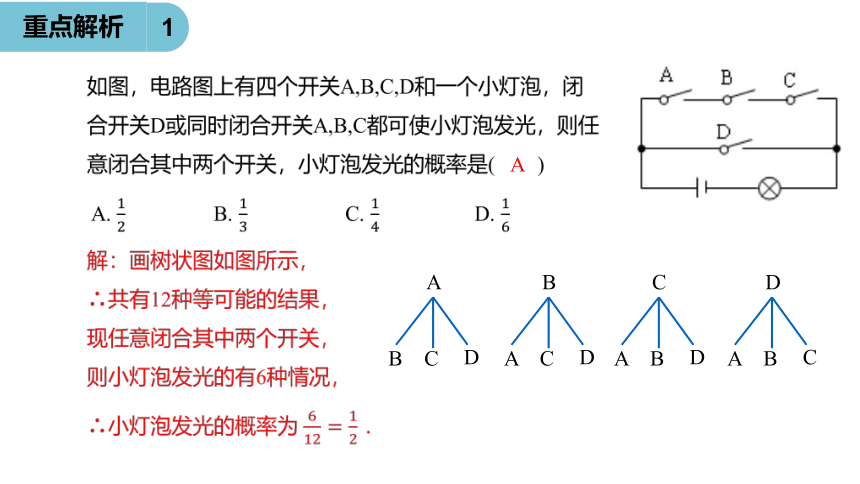
如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是(
)
A.
B.
C.
D.
A
解:画树状图如图所示,
∴共有12种等可能的结果,
现任意闭合其中两个开关,
则小灯泡发光的有6种情况,
∴小灯泡发光的概率为
.
A
B
C
D
B
A
C
D
C
A
B
D
D
A
B
C
重点解析
2
如图所示,有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)
写出k为负数的概率;
(2)
求一次函数y=kx+b的图象经过二、三、四象限的概率.
解:(1)
因为-1,-2,3中有两个负数,
故k为负数的概率为
.
重点解析
2
如图所示,有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)
写出k为负数的概率;
(2)
求一次函数y=kx+b的图象经过二、三、四象限的概率.
(2)
画树状图如图:
由树状图可知,k、b的取值共有6种情况,
其中k<0且b<0的情况有2种,
∴P(一次函数y=kx+b的图象经过第二、三、四象限)=
.
-1
-2
3
-2
-1
3
3
-2
-1
第一次
第二次
用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,下列说法正确的是( )
A.种植10棵幼树,结果一定是“有9棵幼树成活”
B.种植100棵幼树,结果一定是“90棵幼树成活”和“10棵幼树不成活”
C.种植10n棵幼树,恰好有“n棵幼树不成活”
D.种植
n
棵幼树,当
n
越来越大时,种植成活幼树的频率会越来越稳定于0.9
重点解析
3
D
解:用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,是在大量重复实验中得到的概率的近似值,
故A,B,C错误,D正确.
重点解析
4
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在15%和45%,则布袋中白色球的个数最有可能是(
)
A.24个
B.18个
C.16个
D.6个
C
解:∵摸到红色球、黑色球的频率稳定在15%和45%,
∴摸到白球的频率为
1-15%-45%=40%,
故口袋中白色球的个数可能是
40×40%=16(个).
重点解析
5
在一个不透明的口袋里有分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)
请你用列表或画树状图的方法,表示出所有可能出现的结果;
解:(1)
列表或画树状图如下:
所以共有9种等可能结果.
2
6
7
8
4
6
7
8
6
6
7
8
6
7
8
2
(2,6)
(2,7)
(2,8)
4
(4,6)
(4,7)
(4,8)
6
(6,6)
(6,7)
(6,8)
卡片
小球
重点解析
5
在一个不透明的口袋里有分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(2)
小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
解:(2)规则1:P(小红赢)=
;规则2:P(小红赢)=
,
所以小红选择规则1.
深化练习
1
一个袋中装有2个黑球3个白球,这些球除颜色外,大小、形状、质地完全相同,随机的从这个袋子中摸出一个球不放回,再随机的从这个袋子中摸出一个球,两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
A
黑1
黑2
白1
白2
白3
黑1
—
(黑2,黑1)
(白1,黑1)
(白2,黑1)
(白3,黑1)
黑2
(黑1,黑2)
—
(白1,黑2)
(白2,黑2)
(白3,黑2)
白1
(黑1,白1)
(黑2,白1)
—
(白2,白1)
(白3,白1)
白2
(黑1,白2)
(黑2,白2)
(白1,白2)
—
(白3,白2)
白3
(黑1,白3)
(黑2,白3)
(白1,白3)
(白2,白3)
—
第一次
第二次
深化练习
2
在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球.如果口袋中装有3个红球且摸到红球的概率为
,那么口袋中球的总个数为_____.
解:设口袋中球的总个数为x,
则摸到红球的概率为
,
所以x=15.
15
深化练习
3
甲、乙两个小型超市举行有奖促销活动,顾客每购满20元就有一次按下面规则转动转盘获奖机会,且两超市奖额等同.规则是:
①甲超市把转盘等分成4个扇形区域、乙超市把转盘等分成3个扇形区域,并标上了数字(如图所示);
②顾客每一回转动转盘要转两次,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).
利用树形图或列表法分别求出甲、
乙两超市顾客转动一回转盘获奖的概率;
1
1
2
2
3
3
4
甲
乙
深化练习
3
解:(1)
列表格如下:
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
第一回
第二回
甲超市
共有16种等可能结果,其中中奖的有8种,
∴P(甲)=
.
1
1
2
2
3
3
4
甲
乙
深化练习
3
1
2
3
1
2
3
4
2
3
4
5
3
4
5
6
第一回
第二回
乙超市
∴P(乙)=
.
共有9种等可能结果,其中中奖的有4种;
1
1
2
2
3
3
4
甲
乙
深化练习
3
甲、乙两个小型超市举行有奖促销活动,顾客每购满20元就有一次按下面规则转动转盘获奖机会,且两超市奖额等同.规则是:
①甲超市把转盘等分成4个扇形区域、乙超市把转盘等分成3个扇形区域,并标上了数字(如图所示);
②顾客每一回转动转盘要转两次,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).
(2)
如果只考虑中奖因素,你将会选择去
哪个超市购物?说明理由.
1
1
2
2
3
3
4
甲
乙
解:选甲超市.理由如下:
∵P(甲)>P(乙),
∴选甲超市.
第2课时
25章概率初步小结
知识梳理
概率
求法
应用
直接列举法
列表法
画树状图法
用列举法求概率
用频率估计概率
抽奖问题、游戏是否公平问题等
知识梳理
直接列举法
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,那么出现每一种结果的概率都是
.
如果事件A包括其中的m种可能的结果,那么事件A发生的概率
P(A)
.
m个
(1)
直接列举试验结果时,要有一定的顺序性,保证结果不重不漏.
(2)
用列举法求概率的前提有两个:
①所有可能出现的结果是有限个;②每个结果出现的可能性相等.
知识梳理
列表法
列表法就是用表格的形式反映事件发生的各种结果出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法.
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
知识梳理
树状图法
画树状图法是用树状图的形式反映事件发生的各种结果出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法.
一个试验
第一个因素
第二个因素
A
B
1
2
3
1
2
3
当一次试验涉及两个或更多个因素时,为了不重不漏地列出所有等可能的结果,通常采用画树状图法.
知识梳理
用频率估计概率
从长期实践中,人们观察到对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件发生的频率,总在一个固定数的附近摆动,显示出一定的稳定性.因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
用频率估计概率时,必须做足够多的试验才能使频率趋于稳定,并且每次试验必须在相同条件下进行,试验次数越多,得到的频率值就越接近概率,规律就越明显,此时可以用频率的稳定值估计事件发生的概率.
知识梳理
频率
概率
区别
试验值或使用时的统计值
理论值
与试验次数的变化有关
与试验次数的变化无关
与试验人、试验时间、试验地点有关
与试验人、试验时间、试验地点无关
联系
试验次数越多,频率越趋向于概率
频率与概率的区别和联系
重点解析
1
如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是(
)
A.
B.
C.
D.
A
解:画树状图如图所示,
∴共有12种等可能的结果,
现任意闭合其中两个开关,
则小灯泡发光的有6种情况,
∴小灯泡发光的概率为
.
A
B
C
D
B
A
C
D
C
A
B
D
D
A
B
C
重点解析
2
如图所示,有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)
写出k为负数的概率;
(2)
求一次函数y=kx+b的图象经过二、三、四象限的概率.
解:(1)
因为-1,-2,3中有两个负数,
故k为负数的概率为
.
重点解析
2
如图所示,有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)
写出k为负数的概率;
(2)
求一次函数y=kx+b的图象经过二、三、四象限的概率.
(2)
画树状图如图:
由树状图可知,k、b的取值共有6种情况,
其中k<0且b<0的情况有2种,
∴P(一次函数y=kx+b的图象经过第二、三、四象限)=
.
-1
-2
3
-2
-1
3
3
-2
-1
第一次
第二次
用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,下列说法正确的是( )
A.种植10棵幼树,结果一定是“有9棵幼树成活”
B.种植100棵幼树,结果一定是“90棵幼树成活”和“10棵幼树不成活”
C.种植10n棵幼树,恰好有“n棵幼树不成活”
D.种植
n
棵幼树,当
n
越来越大时,种植成活幼树的频率会越来越稳定于0.9
重点解析
3
D
解:用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,是在大量重复实验中得到的概率的近似值,
故A,B,C错误,D正确.
重点解析
4
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在15%和45%,则布袋中白色球的个数最有可能是(
)
A.24个
B.18个
C.16个
D.6个
C
解:∵摸到红色球、黑色球的频率稳定在15%和45%,
∴摸到白球的频率为
1-15%-45%=40%,
故口袋中白色球的个数可能是
40×40%=16(个).
重点解析
5
在一个不透明的口袋里有分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)
请你用列表或画树状图的方法,表示出所有可能出现的结果;
解:(1)
列表或画树状图如下:
所以共有9种等可能结果.
2
6
7
8
4
6
7
8
6
6
7
8
6
7
8
2
(2,6)
(2,7)
(2,8)
4
(4,6)
(4,7)
(4,8)
6
(6,6)
(6,7)
(6,8)
卡片
小球
重点解析
5
在一个不透明的口袋里有分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(2)
小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
解:(2)规则1:P(小红赢)=
;规则2:P(小红赢)=
,
所以小红选择规则1.
深化练习
1
一个袋中装有2个黑球3个白球,这些球除颜色外,大小、形状、质地完全相同,随机的从这个袋子中摸出一个球不放回,再随机的从这个袋子中摸出一个球,两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
A
黑1
黑2
白1
白2
白3
黑1
—
(黑2,黑1)
(白1,黑1)
(白2,黑1)
(白3,黑1)
黑2
(黑1,黑2)
—
(白1,黑2)
(白2,黑2)
(白3,黑2)
白1
(黑1,白1)
(黑2,白1)
—
(白2,白1)
(白3,白1)
白2
(黑1,白2)
(黑2,白2)
(白1,白2)
—
(白3,白2)
白3
(黑1,白3)
(黑2,白3)
(白1,白3)
(白2,白3)
—
第一次
第二次
深化练习
2
在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球.如果口袋中装有3个红球且摸到红球的概率为
,那么口袋中球的总个数为_____.
解:设口袋中球的总个数为x,
则摸到红球的概率为
,
所以x=15.
15
深化练习
3
甲、乙两个小型超市举行有奖促销活动,顾客每购满20元就有一次按下面规则转动转盘获奖机会,且两超市奖额等同.规则是:
①甲超市把转盘等分成4个扇形区域、乙超市把转盘等分成3个扇形区域,并标上了数字(如图所示);
②顾客每一回转动转盘要转两次,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).
利用树形图或列表法分别求出甲、
乙两超市顾客转动一回转盘获奖的概率;
1
1
2
2
3
3
4
甲
乙
深化练习
3
解:(1)
列表格如下:
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
第一回
第二回
甲超市
共有16种等可能结果,其中中奖的有8种,
∴P(甲)=
.
1
1
2
2
3
3
4
甲
乙
深化练习
3
1
2
3
1
2
3
4
2
3
4
5
3
4
5
6
第一回
第二回
乙超市
∴P(乙)=
.
共有9种等可能结果,其中中奖的有4种;
1
1
2
2
3
3
4
甲
乙
深化练习
3
甲、乙两个小型超市举行有奖促销活动,顾客每购满20元就有一次按下面规则转动转盘获奖机会,且两超市奖额等同.规则是:
①甲超市把转盘等分成4个扇形区域、乙超市把转盘等分成3个扇形区域,并标上了数字(如图所示);
②顾客每一回转动转盘要转两次,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).
(2)
如果只考虑中奖因素,你将会选择去
哪个超市购物?说明理由.
1
1
2
2
3
3
4
甲
乙
解:选甲超市.理由如下:
∵P(甲)>P(乙),
∴选甲超市.
同课章节目录
