2019-2020学年黑龙江省齐齐哈尔市甘南县七年级下学期期中数学试卷(五四学制) (解析版)
文档属性
| 名称 | 2019-2020学年黑龙江省齐齐哈尔市甘南县七年级下学期期中数学试卷(五四学制) (解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 316.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 21:48:31 | ||
图片预览



文档简介
2019-2020学年七年级第二学期期中数学试卷(五四学制)
一、选择题(共10小题)
1.下列各图中,∠1与∠2是对顶角的是( )
A.
B.
C.
D.
2.的平方根是( )
A.2
B.±2
C.
D.±
3.如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6
B.∠2=∠6
C.∠1=∠3
D.∠5=∠7
4.在实数,,,0,﹣1.414,,,0.1010010001中,无理数有( )
A.2个
B.3个
C.4个
D.5个
5.平面直角坐标系中,点A(﹣2,a)位于x轴的上方,则a的值可以是( )
A.0
B.﹣1
C.
D.±3
6.如图,射线OC的端点O在直线AB上,∠1的度数x°是∠2的度数y°的2倍多10°,则可列正确的方程组为( )
A.
B.
C.
D.
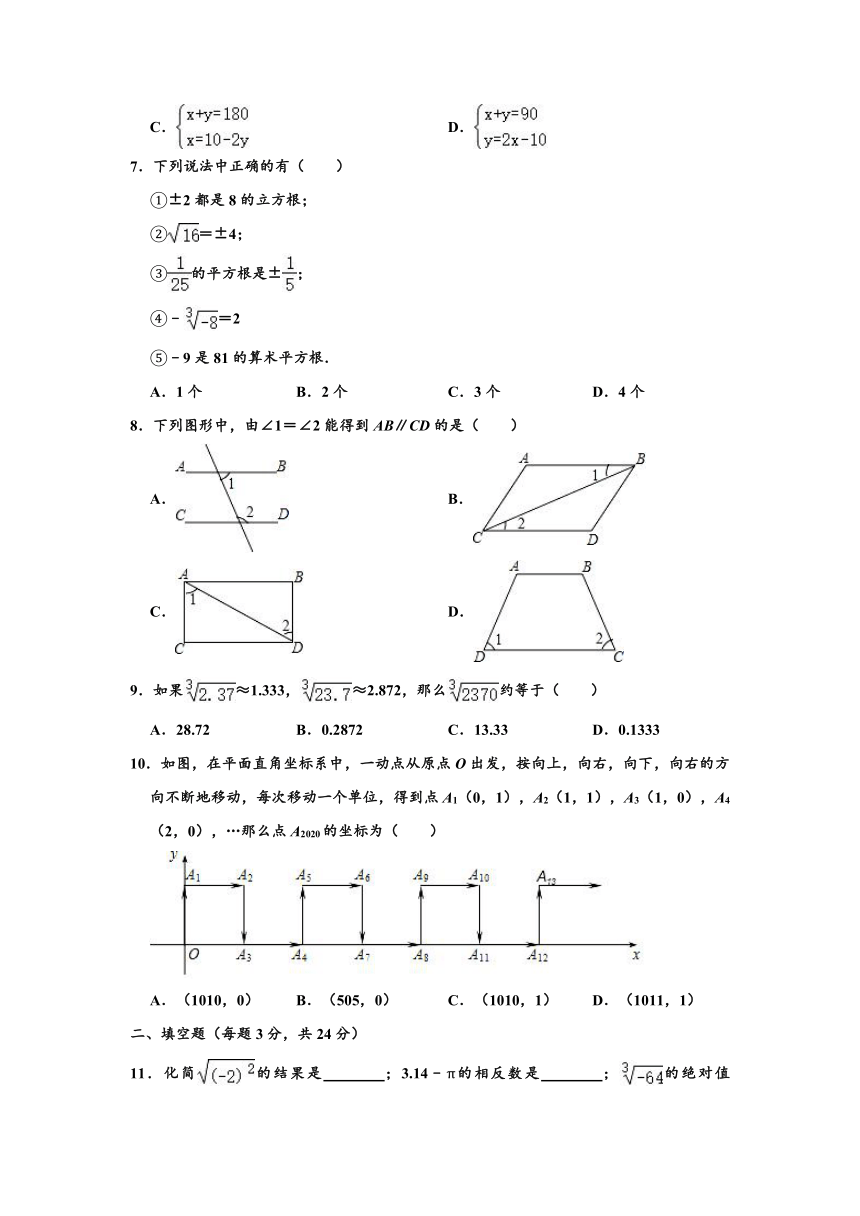
7.下列说法中正确的有( )
①±2都是8的立方根;
②=±4;
③的平方根是±;
④﹣=2
⑤﹣9是81的算术平方根.
A.1个
B.2个
C.3个
D.4个
8.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.
B.
C.
D.
9.如果≈1.333,≈2.872,那么约等于( )
A.28.72
B.0.2872
C.13.33
D.0.1333
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2020的坐标为( )
A.(1010,0)
B.(505,0)
C.(1010,1)
D.(1011,1)
二、填空题(每题3分,共24分)
11.化简的结果是
;3.14﹣π的相反数是
;的绝对值是
.
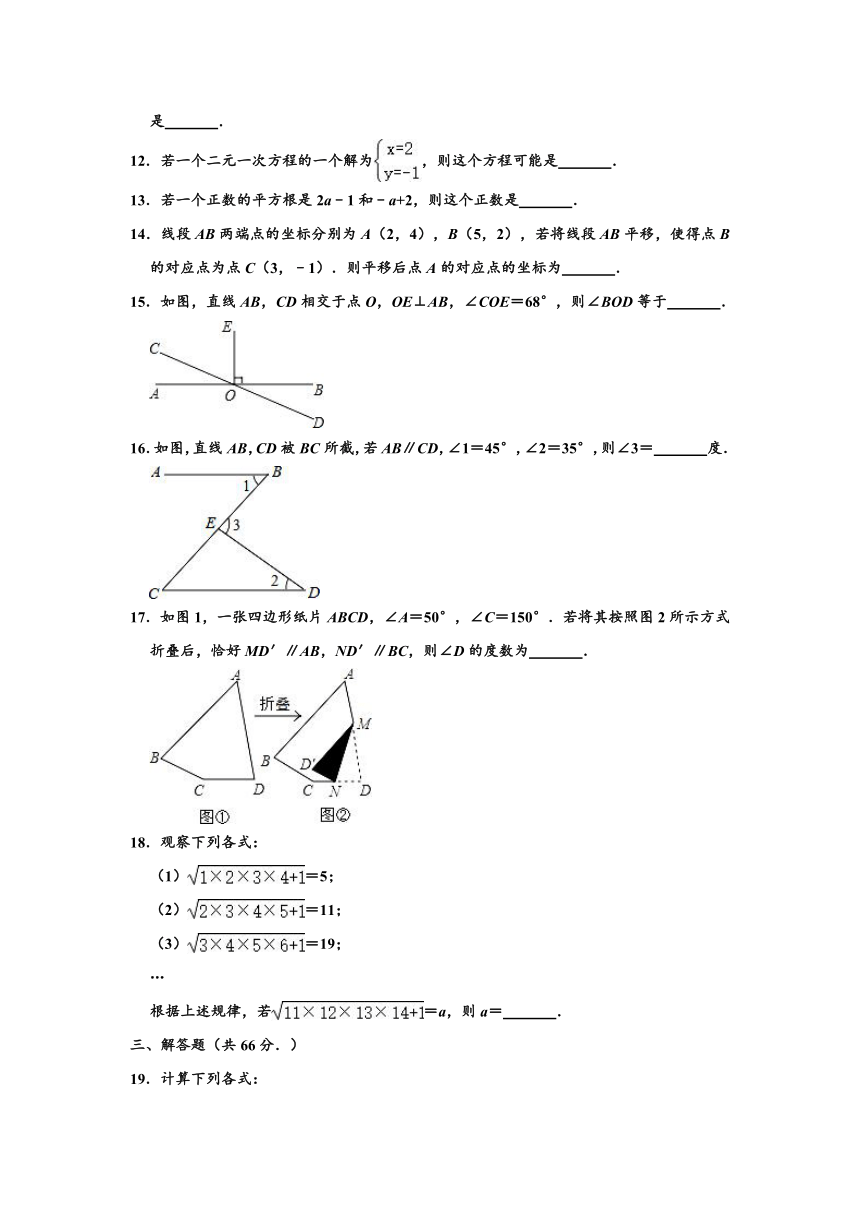
12.若一个二元一次方程的一个解为,则这个方程可能是
.
13.若一个正数的平方根是2a﹣1和﹣a+2,则这个正数是
.
14.线段AB两端点的坐标分别为A(2,4),B(5,2),若将线段AB平移,使得点B的对应点为点C(3,﹣1).则平移后点A的对应点的坐标为
.
15.如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD等于
.
16.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=
度.
17.如图1,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图2所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为
.
18.观察下列各式:
(1)=5;
(2)=11;
(3)=19;
…
根据上述规律,若=a,则a=
.
三、解答题(共66分.)
19.计算下列各式:
(1)﹣++
(2)|1﹣|+×﹣
20.解下列方程(组)
(1)64x3+27=0
(2)
(3)
21.如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1
,B1
,C1
;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
22.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知),
∴∠2=
(
),
又∵∠1=∠2(已知),
∴∠1=∠3(
),
∴AB∥
(
),
∴∠BAC+
=180°(
),
∵∠BAC=70°(已知),
∴∠AGD=
.
23.某工地调来72人参加挖土和运土,已知3人挖出的土1人恰好全部运走,怎样调配劳力才能使挖出来的土能及时运走且不窝工?
24.问题情景:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:
过点P作PE∥AB,
∴∠PAB+∠APE=180°.
∵∠PAB=130°,∴∠APE=50°
∵AB∥CD,PE∥AB,∴PE∥CD,
∴∠PCD+∠CPE=180°.
∵∠PCD=120°,∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
如果AB与CD平行关系不变,动点P在直线AB、CD所夹区域内部运动时,∠PAB,∠PCD的度数会跟着发生变化.
(1)如图3,当动点P运动到直线AC右侧时,请写出∠PAB,∠PCD和∠APC之间的数量关系?并说明理由
(2)如图4,AQ,CQ分别平分∠PAB,∠PCD,那么∠AQC和角∠APC有怎择的数量关系?
(3)如图5,点P在直线AC的左侧时,AQ,CQ仍然平分∠PAB,∠PCD,请直接写出∠AQC和角∠APC的数量关系
.
参考答案
一、单项选择题(每小题3分,共30分.每小题只有一个选项是正确的)
1.下列各图中,∠1与∠2是对顶角的是( )
A.
B.
C.
D.
【分析】根据对顶角的定义逐个判断即可.
解:A、∠1与∠2不是对顶角,故本选项不符合题意;
B、∠1与∠2不是对顶角,故本选项不符合题意;
C、∠1与∠2是对顶角,故本选项符合题意;
D、∠1与∠2不是对顶角,故本选项不符合题意;
故选:C.
【点评】本题考查了对顶角的定义,能理解对顶角的定义的内容是解此题的关键.
2.的平方根是( )
A.2
B.±2
C.
D.±
【分析】先化简,然后再根据平方根的定义求解即可.
解:∵=2,
∴的平方根是±.
故选:D.
【点评】本题考查了平方根的定义以及算术平方根,先把正确化简是解题的关键,本题比较容易出错.
3.如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6
B.∠2=∠6
C.∠1=∠3
D.∠5=∠7
【分析】利用平行线的判定方法判断即可.
解:∵∠2=∠6(已知),
∴a∥b(同位角相等,两直线平行),
则能使a∥b的条件是∠2=∠6,
故选:B.
【点评】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
4.在实数,,,0,﹣1.414,,,0.1010010001中,无理数有( )
A.2个
B.3个
C.4个
D.5个
【分析】利用无理数的定义判断即可.
解:无理数有:,,共2个,
故选:A.
【点评】此题考查了无理数,算术平方根,以及立方根,弄清无理数的定义是解本题的关键.
5.平面直角坐标系中,点A(﹣2,a)位于x轴的上方,则a的值可以是( )
A.0
B.﹣1
C.
D.±3
【分析】根据平面直角坐标系可得a为正数,进而可选出答案.
解:∵点A(﹣2,a)位于x轴的上方,
∴a为正数,
故选:C.
【点评】此题主要考查了点的坐标,关键是掌握x轴的上方的点的纵坐标为正,x轴的下方的点的纵坐标为负.
6.如图,射线OC的端点O在直线AB上,∠1的度数x°是∠2的度数y°的2倍多10°,则可列正确的方程组为( )
A.
B.
C.
D.
【分析】根据∠1与∠2互为邻补角及∠1的度数x°是∠2的度数y°的2倍多10°可列出方程组.
解:设∠1的度数为x°,∠2的度数为y°,则
.
故选:B.
【点评】本题考查由实际问题抽象出二元一次方程组,根据两个角的和为平角和两角的大小关系列出方程组.
7.下列说法中正确的有( )
①±2都是8的立方根;
②=±4;
③的平方根是±;
④﹣=2
⑤﹣9是81的算术平方根.
A.1个
B.2个
C.3个
D.4个
【分析】直接利用立方根以及平方根和算术平方根的定义进而分析得出答案.
解:①2都是8的立方根,故此选项错误;
②=4,故此选项错误;
③的平方根是±,正确;
④﹣=2,正确;
⑤9是81的算术平方根,故此选项错误.
故选:B.
【点评】此题主要考查了立方根以及平方根和算术平方根的定义,正确把握定义是解题关键.
8.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.
B.
C.
D.
【分析】利用平行线的判定方法判断即可.
解:如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选:B.
【点评】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
9.如果≈1.333,≈2.872,那么约等于( )
A.28.72
B.0.2872
C.13.33
D.0.1333
【分析】根据立方根,即可解答.
解:∵≈1.333,
∴=≈1.333×10=13.33.
故选:C.
【点评】本题考查了立方根,解决本题的关键是熟记立方根的定义.
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2020的坐标为( )
A.(1010,0)
B.(505,0)
C.(1010,1)
D.(1011,1)
【分析】根据图形可找出点A4、A8、A12、…的坐标,根据点的坐标的变化可找出变化规律:A4n(2n,1)(n为自然数),依此规律即可得出结论.
解:观察图形可知:A4(2,0),A8(4,0),A12(6,0),…,
∴A4n(2n,1)(n为自然数),
∵2020÷4=505,
∴A2017(1010,0).
故选:A.
【点评】本题考查了规律型中点的坐标,根据点的变化找出变化规律:A4n(2n,0)(n为自然数)是解题的关键.
二、填空题(每题3分,共24分)
11.化简的结果是 2 ;3.14﹣π的相反数是 π﹣3.14 ;的绝对值是 4 .
【分析】直接利用二次根式的性质以及相反数的定义、绝对值的性质分别得出答案.
解:=2;
3.14﹣π的相反数是:π﹣3.14;
=﹣4的绝对值是:4.
故答案为:2,π﹣3.14,4.
【点评】此题主要考查了算术平方根以及立方根,正确把握相关定义是解题关键.
12.若一个二元一次方程的一个解为,则这个方程可能是 x+y=1 .
【分析】方程的解是,把x=2,y=1代入方程,方程的左右两边一定相等,据此即可求解.
解:这个方程可能是:x+y=1,答案不唯一.
故答案是:x+y=1,答案不唯一.
【点评】考查二元一次方程的解的定义,要求理解什么是二元一次方程的解,并会把x,y的值代入原方程验证二元一次方程的解.
13.若一个正数的平方根是2a﹣1和﹣a+2,则这个正数是 9 .
【分析】首先根据整数有两个平方根,它们互为相反数可得2a﹣1﹣a+2=0,解方程可得a,然后再求出这个正数即可.
解:由题意得:2a﹣1﹣a+2=0,
解得:a=﹣1,
2a﹣1=﹣3,﹣a+2=3,
∵9的算术平方根为±3,
∴这个正数为9,
故答案为:9.
【点评】此题主要考查了平方根,关键是掌握一个正数有两个平方根,这两个平方根互为相反数.
14.线段AB两端点的坐标分别为A(2,4),B(5,2),若将线段AB平移,使得点B的对应点为点C(3,﹣1).则平移后点A的对应点的坐标为 (0,1) .
【分析】先得到点B的对应规律,依此得到A的坐标即可.
解:∵B(5,2),点B的对应点为点C(3,﹣1).
∴变化规律是横坐标减2,纵坐标减3,
∵A(2,4),
∴平移后点A的对应点的坐标为
(0,1),
故答案为(0,1).
【点评】考查点的平移变换;得到一对对应点的变换规律是解决本题的关键.
15.如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD等于 22° .
【分析】根据垂直的定义求得∠AOE=90°;然后根据余角的定义可以推知∠AOC=∠AOE﹣∠COE=22°;最后由对顶角的性质可以求得∠BOD=∠AOC=22°.
解:∵OE⊥AB,
∴∠AOE=90°;
又∵∠COE=68°,
∴∠AOC=∠AOE﹣∠COE=22°,
∴∠BOD=∠AOC=22°(对顶角相等);
故答案是:22°.
【点评】本题考查了垂线、对顶角与邻补角.注意,此题中隐含着已知条件“∠AOE=90°”.
16.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= 80 度.
【分析】根据平行线的性质求出∠C,根据三角形外角性质求出即可.
解:∵AB∥CD,∠1=45°,
∴∠C=∠1=45°,
∵∠2=35°,
∴∠3=∠2+∠C=35°+45°=80°,
故答案为:80.
【点评】本题考查了平行线的性质,三角形的外角性质的应用,解此题的关键是求出∠C的度数和得出∠3=∠2+∠C.
17.如图1,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图2所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 80° .
【分析】先根据翻折变换的性质得出∠1=∠D′MN,∠2=∠D′NM,再由平行线的性质求出∠1+∠=∠D′MN及∠2+∠D′NM的度数,进而可得出结论.
解:∵△MND′由△MND翻折而成,
∴∠1=∠D′MN,∠2=∠D′NM,
∵MD′∥AB,ND′∥BC,∠A=50°,∠C=150°
∴∠1+∠D′MN=∠A=50°,∠2+∠D′NM=∠C=150°,
∴∠1=∠D′MN=∠A==25°,∠2=∠D′NM=∠C==75°,
∴∠D=180°﹣∠1﹣∠2=180°﹣25°﹣75°=80°.
故答案是:80°.
【点评】本题考查的是翻折变换的性质及平行线的性质,解答此类题目时往往隐含了三角形的内角和是180°这一知识点.
18.观察下列各式:
(1)=5;
(2)=11;
(3)=19;
…
根据上述规律,若=a,则a= 155 .
【分析】根据前面几个算式的值,推演出规律后计算的值.
解:
=11×14+1
=154+1
=155.
故答案为:155.
【点评】本题考查了有理数的运算,属于规律型题目,解答本题的关键是总结规律,难度较大.
三、解答题(共66分.)
19.计算下列各式:
(1)﹣++
(2)|1﹣|+×﹣
【分析】(1)原式利用平方根、立方根定义计算即可求出值;
(2)原式利用绝对值的代数意义,平方根、立方根定义计算即可求出值.
解:(1)原式=4﹣3﹣+
=2;
(2)原式=﹣1﹣×﹣
=﹣.
【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
20.解下列方程(组)
(1)64x3+27=0
(2)
(3)
【分析】(1)方程整理后,利用立方根定义开立方即可求出解;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可.
解:(1)方程整理得:x3=﹣,
开立方得:x=﹣;
(2),
①×3﹣②得:2x=8,
解得:x=4,
把x=4代入①得:y=﹣3,
则方程组的解为;
(3)方程组整理得:,
①+②得:6x=18,
解得:x=3,
②﹣①得:4y=2,
解得:y=,
则方程组的解为.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
21.如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 (4,7) ,B1 (1,2) ,C1 (6,4) ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
【分析】(1)先画出平移后的图形,结合直角坐标系可得出三点坐标;
(2)根据平移的特点,分别找到各点的对应点,顺次连接即可得出答案;
(3)将△ABC补全为矩形,然后利用作差法求解即可.
解:(1)结合所画图形可得:A1坐标为(4,7),点B1坐标为(1,2),C1坐标为(6,4).
(2)所画图形如下:
(3)
S△ABC=S矩形EBGF﹣S△ABE﹣S△GBC﹣S△AFC=25﹣﹣5﹣3=.
【点评】本题考查了平移作图的知识,解答本题的关键是根据平移的特点准确作出图形,第三问的解题方法同学们可以参考一下,求解不规则图形面积的时候可以先补全,再减去.
22.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知),
∴∠2= ∠3 ( 两直线平行,同位角相等 ),
又∵∠1=∠2(已知),
∴∠1=∠3( 等量代换 ),
∴AB∥ DG ( 内错角相等,两直线平行 ),
∴∠BAC+ ∠AGD =180°( 两直线平行,同旁内角互补 ),
∵∠BAC=70°(已知),
∴∠AGD= 110° .
【分析】由EF与AD平行,利用两直线平行,同位角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到AB与DG平行,利用两直线平行同旁内角互补得到两个角互补,即可求出所求角的度数.
解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°(已知),
∴∠AGD=110°.
故答案为:∠3;两直线平行,同位角相等;等量代换;DG,内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°.
【点评】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
23.某工地调来72人参加挖土和运土,已知3人挖出的土1人恰好全部运走,怎样调配劳力才能使挖出来的土能及时运走且不窝工?
【分析】设有x名员工挖土,根据某工地调来72名员工挖土和运土,已知3人挖的1人恰好能全部运走,调配员工使挖出的土能够及时运走,可列出方程,进而求出即可.
解:设x人挖土,y人运土,由题意可得出:
,
解得:.
答:54人挖土,18人运土,才能使挖出来的土能及时运走且不窝工.
【点评】本题考查了二元一次方程组的应用,根据调配员工使挖出的土能够及时运走得出方程是解题关键.
24.问题情景:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:
过点P作PE∥AB,
∴∠PAB+∠APE=180°.
∵∠PAB=130°,∴∠APE=50°
∵AB∥CD,PE∥AB,∴PE∥CD,
∴∠PCD+∠CPE=180°.
∵∠PCD=120°,∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
如果AB与CD平行关系不变,动点P在直线AB、CD所夹区域内部运动时,∠PAB,∠PCD的度数会跟着发生变化.
(1)如图3,当动点P运动到直线AC右侧时,请写出∠PAB,∠PCD和∠APC之间的数量关系?并说明理由
(2)如图4,AQ,CQ分别平分∠PAB,∠PCD,那么∠AQC和角∠APC有怎择的数量关系?
(3)如图5,点P在直线AC的左侧时,AQ,CQ仍然平分∠PAB,∠PCD,请直接写出∠AQC和角∠APC的数量关系 2∠AQC+∠APC=360° .
【分析】(1)过点P作PF∥AB,利用平行线的性质可得∠PAB+∠PCD=∠APF+∠CPF=∠APC,即∠PAB+∠PCD=∠APC;
(2)依据角平分线即可得到∠QAB+∠QCD=∠PAB+∠PCD=(∠PAB+∠PCD),由(1)可得∠PAB+∠PCD=∠APC,∠QAB+∠QCD=∠AQC,进而得到∠AQC=∠APC;
(3)过点P作PG∥AB,利用平行线的性质以及角平分线的定义,结合(1)中的结论即可得出∠AQC和角∠APC的数量关系.
解:(1)∠PAB+∠PCD=∠APC;
理由:如图3,过点P作PF∥AB,
∴∠PAB=∠APF,
∵AB∥CD,PF∥AB,
∴PF∥CD,
∴∠PCD=∠CPF,
∴∠PAB+∠PCD=∠APF+∠CPF=∠APC,
即∠PAB+∠PCD=∠APC;
(2)∠AQC=∠APC.
理由:如图4,∵AQ,CQ分别平分∠PAB,∠PCD,
∴∠QAB=∠PAB,∠QCD=∠PCD,
∴∠QAB+∠QCD=∠PAB+∠PCD=(∠PAB+∠PCD),
由(1),可得∠PAB+∠PCD=∠APC,
∠QAB+∠QCD=∠AQC,
∴∠AQC=∠APC;
(3)2∠AQC+∠APC=360°;
理由:如图5,过点P作PG∥AB,
∴∠PAB+∠APG=180°,
∵AB∥CD,PG∥AB,
∴PG∥CD,
∴∠PCD+∠CPG=180°,
∴∠PAB+∠APG+∠PCD+∠CPG=360°,
∴∠PAB+∠PCD+∠APC=360°,
∵AQ,CQ分别平分∠PAB,∠PCD,
∴∠QAB=∠PAB,∠QCD=∠PCD,
∴∠QAB+∠QCD=∠PAB+∠PCD=(∠PAB+PCD),
由(1)知,∠QAB+∠QCD=∠AQC,
∴∠AQC=(∠PAB+∠PCD),
2∠AQC=∠PAB+∠PCD,
∵∠PAB+∠PCD+∠APC=360°,
∴2∠AQC+∠APC=360°.
故答案为:2∠AQC+∠APC=360°.
【点评】本题考查了平行线的性质,平行公理的应用,解决此类题目,过拐点作平行线是解题的关键.
一、选择题(共10小题)
1.下列各图中,∠1与∠2是对顶角的是( )
A.
B.
C.
D.
2.的平方根是( )
A.2
B.±2
C.
D.±
3.如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6
B.∠2=∠6
C.∠1=∠3
D.∠5=∠7
4.在实数,,,0,﹣1.414,,,0.1010010001中,无理数有( )
A.2个
B.3个
C.4个
D.5个
5.平面直角坐标系中,点A(﹣2,a)位于x轴的上方,则a的值可以是( )
A.0
B.﹣1
C.
D.±3
6.如图,射线OC的端点O在直线AB上,∠1的度数x°是∠2的度数y°的2倍多10°,则可列正确的方程组为( )
A.
B.
C.
D.
7.下列说法中正确的有( )
①±2都是8的立方根;
②=±4;
③的平方根是±;
④﹣=2
⑤﹣9是81的算术平方根.
A.1个
B.2个
C.3个
D.4个
8.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.
B.
C.
D.
9.如果≈1.333,≈2.872,那么约等于( )
A.28.72
B.0.2872
C.13.33
D.0.1333
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2020的坐标为( )
A.(1010,0)
B.(505,0)
C.(1010,1)
D.(1011,1)
二、填空题(每题3分,共24分)
11.化简的结果是
;3.14﹣π的相反数是
;的绝对值是
.
12.若一个二元一次方程的一个解为,则这个方程可能是
.
13.若一个正数的平方根是2a﹣1和﹣a+2,则这个正数是
.
14.线段AB两端点的坐标分别为A(2,4),B(5,2),若将线段AB平移,使得点B的对应点为点C(3,﹣1).则平移后点A的对应点的坐标为
.
15.如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD等于
.
16.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=
度.
17.如图1,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图2所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为
.
18.观察下列各式:
(1)=5;
(2)=11;
(3)=19;
…
根据上述规律,若=a,则a=
.
三、解答题(共66分.)
19.计算下列各式:
(1)﹣++
(2)|1﹣|+×﹣
20.解下列方程(组)
(1)64x3+27=0
(2)
(3)
21.如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1
,B1
,C1
;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
22.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知),
∴∠2=
(
),
又∵∠1=∠2(已知),
∴∠1=∠3(
),
∴AB∥
(
),
∴∠BAC+
=180°(
),
∵∠BAC=70°(已知),
∴∠AGD=
.
23.某工地调来72人参加挖土和运土,已知3人挖出的土1人恰好全部运走,怎样调配劳力才能使挖出来的土能及时运走且不窝工?
24.问题情景:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:
过点P作PE∥AB,
∴∠PAB+∠APE=180°.
∵∠PAB=130°,∴∠APE=50°
∵AB∥CD,PE∥AB,∴PE∥CD,
∴∠PCD+∠CPE=180°.
∵∠PCD=120°,∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
如果AB与CD平行关系不变,动点P在直线AB、CD所夹区域内部运动时,∠PAB,∠PCD的度数会跟着发生变化.
(1)如图3,当动点P运动到直线AC右侧时,请写出∠PAB,∠PCD和∠APC之间的数量关系?并说明理由
(2)如图4,AQ,CQ分别平分∠PAB,∠PCD,那么∠AQC和角∠APC有怎择的数量关系?
(3)如图5,点P在直线AC的左侧时,AQ,CQ仍然平分∠PAB,∠PCD,请直接写出∠AQC和角∠APC的数量关系
.
参考答案
一、单项选择题(每小题3分,共30分.每小题只有一个选项是正确的)
1.下列各图中,∠1与∠2是对顶角的是( )
A.
B.
C.
D.
【分析】根据对顶角的定义逐个判断即可.
解:A、∠1与∠2不是对顶角,故本选项不符合题意;
B、∠1与∠2不是对顶角,故本选项不符合题意;
C、∠1与∠2是对顶角,故本选项符合题意;
D、∠1与∠2不是对顶角,故本选项不符合题意;
故选:C.
【点评】本题考查了对顶角的定义,能理解对顶角的定义的内容是解此题的关键.
2.的平方根是( )
A.2
B.±2
C.
D.±
【分析】先化简,然后再根据平方根的定义求解即可.
解:∵=2,
∴的平方根是±.
故选:D.
【点评】本题考查了平方根的定义以及算术平方根,先把正确化简是解题的关键,本题比较容易出错.
3.如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6
B.∠2=∠6
C.∠1=∠3
D.∠5=∠7
【分析】利用平行线的判定方法判断即可.
解:∵∠2=∠6(已知),
∴a∥b(同位角相等,两直线平行),
则能使a∥b的条件是∠2=∠6,
故选:B.
【点评】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
4.在实数,,,0,﹣1.414,,,0.1010010001中,无理数有( )
A.2个
B.3个
C.4个
D.5个
【分析】利用无理数的定义判断即可.
解:无理数有:,,共2个,
故选:A.
【点评】此题考查了无理数,算术平方根,以及立方根,弄清无理数的定义是解本题的关键.
5.平面直角坐标系中,点A(﹣2,a)位于x轴的上方,则a的值可以是( )
A.0
B.﹣1
C.
D.±3
【分析】根据平面直角坐标系可得a为正数,进而可选出答案.
解:∵点A(﹣2,a)位于x轴的上方,
∴a为正数,
故选:C.
【点评】此题主要考查了点的坐标,关键是掌握x轴的上方的点的纵坐标为正,x轴的下方的点的纵坐标为负.
6.如图,射线OC的端点O在直线AB上,∠1的度数x°是∠2的度数y°的2倍多10°,则可列正确的方程组为( )
A.
B.
C.
D.
【分析】根据∠1与∠2互为邻补角及∠1的度数x°是∠2的度数y°的2倍多10°可列出方程组.
解:设∠1的度数为x°,∠2的度数为y°,则
.
故选:B.
【点评】本题考查由实际问题抽象出二元一次方程组,根据两个角的和为平角和两角的大小关系列出方程组.
7.下列说法中正确的有( )
①±2都是8的立方根;
②=±4;
③的平方根是±;
④﹣=2
⑤﹣9是81的算术平方根.
A.1个
B.2个
C.3个
D.4个
【分析】直接利用立方根以及平方根和算术平方根的定义进而分析得出答案.
解:①2都是8的立方根,故此选项错误;
②=4,故此选项错误;
③的平方根是±,正确;
④﹣=2,正确;
⑤9是81的算术平方根,故此选项错误.
故选:B.
【点评】此题主要考查了立方根以及平方根和算术平方根的定义,正确把握定义是解题关键.
8.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.
B.
C.
D.
【分析】利用平行线的判定方法判断即可.
解:如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选:B.
【点评】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
9.如果≈1.333,≈2.872,那么约等于( )
A.28.72
B.0.2872
C.13.33
D.0.1333
【分析】根据立方根,即可解答.
解:∵≈1.333,
∴=≈1.333×10=13.33.
故选:C.
【点评】本题考查了立方根,解决本题的关键是熟记立方根的定义.
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2020的坐标为( )
A.(1010,0)
B.(505,0)
C.(1010,1)
D.(1011,1)
【分析】根据图形可找出点A4、A8、A12、…的坐标,根据点的坐标的变化可找出变化规律:A4n(2n,1)(n为自然数),依此规律即可得出结论.
解:观察图形可知:A4(2,0),A8(4,0),A12(6,0),…,
∴A4n(2n,1)(n为自然数),
∵2020÷4=505,
∴A2017(1010,0).
故选:A.
【点评】本题考查了规律型中点的坐标,根据点的变化找出变化规律:A4n(2n,0)(n为自然数)是解题的关键.
二、填空题(每题3分,共24分)
11.化简的结果是 2 ;3.14﹣π的相反数是 π﹣3.14 ;的绝对值是 4 .
【分析】直接利用二次根式的性质以及相反数的定义、绝对值的性质分别得出答案.
解:=2;
3.14﹣π的相反数是:π﹣3.14;
=﹣4的绝对值是:4.
故答案为:2,π﹣3.14,4.
【点评】此题主要考查了算术平方根以及立方根,正确把握相关定义是解题关键.
12.若一个二元一次方程的一个解为,则这个方程可能是 x+y=1 .
【分析】方程的解是,把x=2,y=1代入方程,方程的左右两边一定相等,据此即可求解.
解:这个方程可能是:x+y=1,答案不唯一.
故答案是:x+y=1,答案不唯一.
【点评】考查二元一次方程的解的定义,要求理解什么是二元一次方程的解,并会把x,y的值代入原方程验证二元一次方程的解.
13.若一个正数的平方根是2a﹣1和﹣a+2,则这个正数是 9 .
【分析】首先根据整数有两个平方根,它们互为相反数可得2a﹣1﹣a+2=0,解方程可得a,然后再求出这个正数即可.
解:由题意得:2a﹣1﹣a+2=0,
解得:a=﹣1,
2a﹣1=﹣3,﹣a+2=3,
∵9的算术平方根为±3,
∴这个正数为9,
故答案为:9.
【点评】此题主要考查了平方根,关键是掌握一个正数有两个平方根,这两个平方根互为相反数.
14.线段AB两端点的坐标分别为A(2,4),B(5,2),若将线段AB平移,使得点B的对应点为点C(3,﹣1).则平移后点A的对应点的坐标为 (0,1) .
【分析】先得到点B的对应规律,依此得到A的坐标即可.
解:∵B(5,2),点B的对应点为点C(3,﹣1).
∴变化规律是横坐标减2,纵坐标减3,
∵A(2,4),
∴平移后点A的对应点的坐标为
(0,1),
故答案为(0,1).
【点评】考查点的平移变换;得到一对对应点的变换规律是解决本题的关键.
15.如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD等于 22° .
【分析】根据垂直的定义求得∠AOE=90°;然后根据余角的定义可以推知∠AOC=∠AOE﹣∠COE=22°;最后由对顶角的性质可以求得∠BOD=∠AOC=22°.
解:∵OE⊥AB,
∴∠AOE=90°;
又∵∠COE=68°,
∴∠AOC=∠AOE﹣∠COE=22°,
∴∠BOD=∠AOC=22°(对顶角相等);
故答案是:22°.
【点评】本题考查了垂线、对顶角与邻补角.注意,此题中隐含着已知条件“∠AOE=90°”.
16.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= 80 度.
【分析】根据平行线的性质求出∠C,根据三角形外角性质求出即可.
解:∵AB∥CD,∠1=45°,
∴∠C=∠1=45°,
∵∠2=35°,
∴∠3=∠2+∠C=35°+45°=80°,
故答案为:80.
【点评】本题考查了平行线的性质,三角形的外角性质的应用,解此题的关键是求出∠C的度数和得出∠3=∠2+∠C.
17.如图1,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图2所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 80° .
【分析】先根据翻折变换的性质得出∠1=∠D′MN,∠2=∠D′NM,再由平行线的性质求出∠1+∠=∠D′MN及∠2+∠D′NM的度数,进而可得出结论.
解:∵△MND′由△MND翻折而成,
∴∠1=∠D′MN,∠2=∠D′NM,
∵MD′∥AB,ND′∥BC,∠A=50°,∠C=150°
∴∠1+∠D′MN=∠A=50°,∠2+∠D′NM=∠C=150°,
∴∠1=∠D′MN=∠A==25°,∠2=∠D′NM=∠C==75°,
∴∠D=180°﹣∠1﹣∠2=180°﹣25°﹣75°=80°.
故答案是:80°.
【点评】本题考查的是翻折变换的性质及平行线的性质,解答此类题目时往往隐含了三角形的内角和是180°这一知识点.
18.观察下列各式:
(1)=5;
(2)=11;
(3)=19;
…
根据上述规律,若=a,则a= 155 .
【分析】根据前面几个算式的值,推演出规律后计算的值.
解:
=11×14+1
=154+1
=155.
故答案为:155.
【点评】本题考查了有理数的运算,属于规律型题目,解答本题的关键是总结规律,难度较大.
三、解答题(共66分.)
19.计算下列各式:
(1)﹣++
(2)|1﹣|+×﹣
【分析】(1)原式利用平方根、立方根定义计算即可求出值;
(2)原式利用绝对值的代数意义,平方根、立方根定义计算即可求出值.
解:(1)原式=4﹣3﹣+
=2;
(2)原式=﹣1﹣×﹣
=﹣.
【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
20.解下列方程(组)
(1)64x3+27=0
(2)
(3)
【分析】(1)方程整理后,利用立方根定义开立方即可求出解;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可.
解:(1)方程整理得:x3=﹣,
开立方得:x=﹣;
(2),
①×3﹣②得:2x=8,
解得:x=4,
把x=4代入①得:y=﹣3,
则方程组的解为;
(3)方程组整理得:,
①+②得:6x=18,
解得:x=3,
②﹣①得:4y=2,
解得:y=,
则方程组的解为.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
21.如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 (4,7) ,B1 (1,2) ,C1 (6,4) ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
【分析】(1)先画出平移后的图形,结合直角坐标系可得出三点坐标;
(2)根据平移的特点,分别找到各点的对应点,顺次连接即可得出答案;
(3)将△ABC补全为矩形,然后利用作差法求解即可.
解:(1)结合所画图形可得:A1坐标为(4,7),点B1坐标为(1,2),C1坐标为(6,4).
(2)所画图形如下:
(3)
S△ABC=S矩形EBGF﹣S△ABE﹣S△GBC﹣S△AFC=25﹣﹣5﹣3=.
【点评】本题考查了平移作图的知识,解答本题的关键是根据平移的特点准确作出图形,第三问的解题方法同学们可以参考一下,求解不规则图形面积的时候可以先补全,再减去.
22.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知),
∴∠2= ∠3 ( 两直线平行,同位角相等 ),
又∵∠1=∠2(已知),
∴∠1=∠3( 等量代换 ),
∴AB∥ DG ( 内错角相等,两直线平行 ),
∴∠BAC+ ∠AGD =180°( 两直线平行,同旁内角互补 ),
∵∠BAC=70°(已知),
∴∠AGD= 110° .
【分析】由EF与AD平行,利用两直线平行,同位角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到AB与DG平行,利用两直线平行同旁内角互补得到两个角互补,即可求出所求角的度数.
解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°(已知),
∴∠AGD=110°.
故答案为:∠3;两直线平行,同位角相等;等量代换;DG,内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°.
【点评】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
23.某工地调来72人参加挖土和运土,已知3人挖出的土1人恰好全部运走,怎样调配劳力才能使挖出来的土能及时运走且不窝工?
【分析】设有x名员工挖土,根据某工地调来72名员工挖土和运土,已知3人挖的1人恰好能全部运走,调配员工使挖出的土能够及时运走,可列出方程,进而求出即可.
解:设x人挖土,y人运土,由题意可得出:
,
解得:.
答:54人挖土,18人运土,才能使挖出来的土能及时运走且不窝工.
【点评】本题考查了二元一次方程组的应用,根据调配员工使挖出的土能够及时运走得出方程是解题关键.
24.问题情景:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:
过点P作PE∥AB,
∴∠PAB+∠APE=180°.
∵∠PAB=130°,∴∠APE=50°
∵AB∥CD,PE∥AB,∴PE∥CD,
∴∠PCD+∠CPE=180°.
∵∠PCD=120°,∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
如果AB与CD平行关系不变,动点P在直线AB、CD所夹区域内部运动时,∠PAB,∠PCD的度数会跟着发生变化.
(1)如图3,当动点P运动到直线AC右侧时,请写出∠PAB,∠PCD和∠APC之间的数量关系?并说明理由
(2)如图4,AQ,CQ分别平分∠PAB,∠PCD,那么∠AQC和角∠APC有怎择的数量关系?
(3)如图5,点P在直线AC的左侧时,AQ,CQ仍然平分∠PAB,∠PCD,请直接写出∠AQC和角∠APC的数量关系 2∠AQC+∠APC=360° .
【分析】(1)过点P作PF∥AB,利用平行线的性质可得∠PAB+∠PCD=∠APF+∠CPF=∠APC,即∠PAB+∠PCD=∠APC;
(2)依据角平分线即可得到∠QAB+∠QCD=∠PAB+∠PCD=(∠PAB+∠PCD),由(1)可得∠PAB+∠PCD=∠APC,∠QAB+∠QCD=∠AQC,进而得到∠AQC=∠APC;
(3)过点P作PG∥AB,利用平行线的性质以及角平分线的定义,结合(1)中的结论即可得出∠AQC和角∠APC的数量关系.
解:(1)∠PAB+∠PCD=∠APC;
理由:如图3,过点P作PF∥AB,
∴∠PAB=∠APF,
∵AB∥CD,PF∥AB,
∴PF∥CD,
∴∠PCD=∠CPF,
∴∠PAB+∠PCD=∠APF+∠CPF=∠APC,
即∠PAB+∠PCD=∠APC;
(2)∠AQC=∠APC.
理由:如图4,∵AQ,CQ分别平分∠PAB,∠PCD,
∴∠QAB=∠PAB,∠QCD=∠PCD,
∴∠QAB+∠QCD=∠PAB+∠PCD=(∠PAB+∠PCD),
由(1),可得∠PAB+∠PCD=∠APC,
∠QAB+∠QCD=∠AQC,
∴∠AQC=∠APC;
(3)2∠AQC+∠APC=360°;
理由:如图5,过点P作PG∥AB,
∴∠PAB+∠APG=180°,
∵AB∥CD,PG∥AB,
∴PG∥CD,
∴∠PCD+∠CPG=180°,
∴∠PAB+∠APG+∠PCD+∠CPG=360°,
∴∠PAB+∠PCD+∠APC=360°,
∵AQ,CQ分别平分∠PAB,∠PCD,
∴∠QAB=∠PAB,∠QCD=∠PCD,
∴∠QAB+∠QCD=∠PAB+∠PCD=(∠PAB+PCD),
由(1)知,∠QAB+∠QCD=∠AQC,
∴∠AQC=(∠PAB+∠PCD),
2∠AQC=∠PAB+∠PCD,
∵∠PAB+∠PCD+∠APC=360°,
∴2∠AQC+∠APC=360°.
故答案为:2∠AQC+∠APC=360°.
【点评】本题考查了平行线的性质,平行公理的应用,解决此类题目,过拐点作平行线是解题的关键.
同课章节目录
