2019-2020学年山东省潍坊市安丘市七年级下学期期中数学试卷 (解析版)
文档属性
| 名称 | 2019-2020学年山东省潍坊市安丘市七年级下学期期中数学试卷 (解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 163.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 05:47:43 | ||
图片预览



文档简介
2019-2020学年七年级第二学期期中数学试卷
一、选择题(共12小题)
1.下列图形中,∠1与∠2是对顶角的有( )
A.
B.
C.
D.
2.下列运算正确的是( )
A.a4+a5=a9
B.a3?a3?a3=3a3
C.2a4?3a5=6a9
D.(﹣a3)4=a7
3.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35°
B.45°
C.55°
D.65°
4.下列命题中是假命题的是( )
A.互补的角不一定是邻补角
B.互补的角若相等,则两个角都是直角
C.一个角的两个邻补角互为对顶角
D.两个锐角的和是锐角
5.已知单项式﹣xm﹣2y3与xny2m﹣3n是同类项,那么m,n的值分别是( )
A.
B.
C.
D.
6.利用加减消元法解方程组,下列做法正确的是( )
A.将①×5﹣②×2可以消去y
B.将①×3+②×(﹣5)可以消去x
C.将①×5+②×3可以消去y
D.将①×(﹣5)+②×2可以消去x
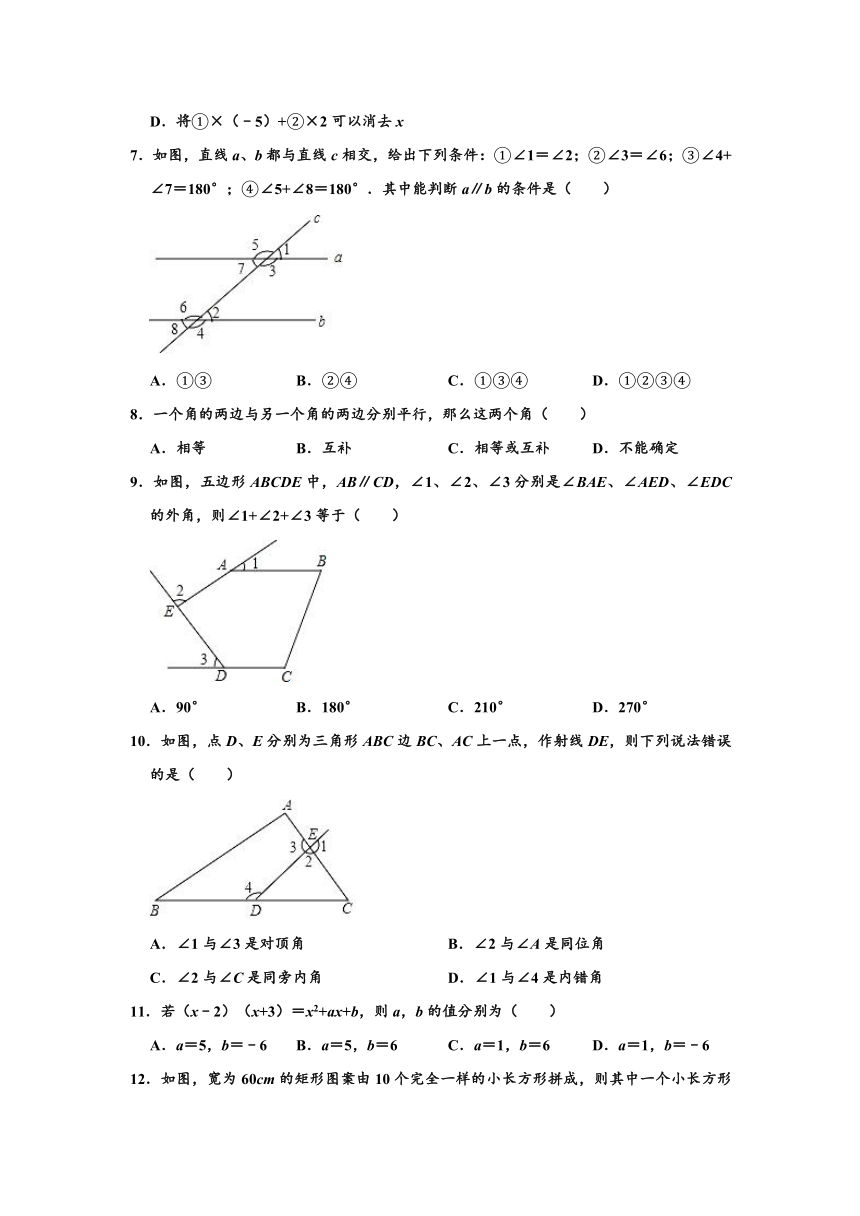
7.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )
A.①③
B.②④
C.①③④
D.①②③④
8.一个角的两边与另一个角的两边分别平行,那么这两个角( )
A.相等
B.互补
C.相等或互补
D.不能确定
9.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A.90°
B.180°
C.210°
D.270°
10.如图,点D、E分别为三角形ABC边BC、AC上一点,作射线DE,则下列说法错误的是( )
A.∠1与∠3是对顶角
B.∠2与∠A是同位角
C.∠2与∠C是同旁内角
D.∠1与∠4是内错角
11.若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=﹣6
B.a=5,b=6
C.a=1,b=6
D.a=1,b=﹣6
12.如图,宽为60cm的矩形图案由10个完全一样的小长方形拼成,则其中一个小长方形的周长为( )
A.60cm
B.120cm
C.312cm
D.576cm
二、填空题(共8小题,共24分,只填写最后结果,每小题填对得3分)
13.一个角是70°39′,则它的余角的度数是
.
14.已知am=6,an=12,则am+n=
.
15.若2x2a﹣b﹣1﹣3y3a+2b﹣16=10是关于x,y的二元一次方程,则a+b=
.
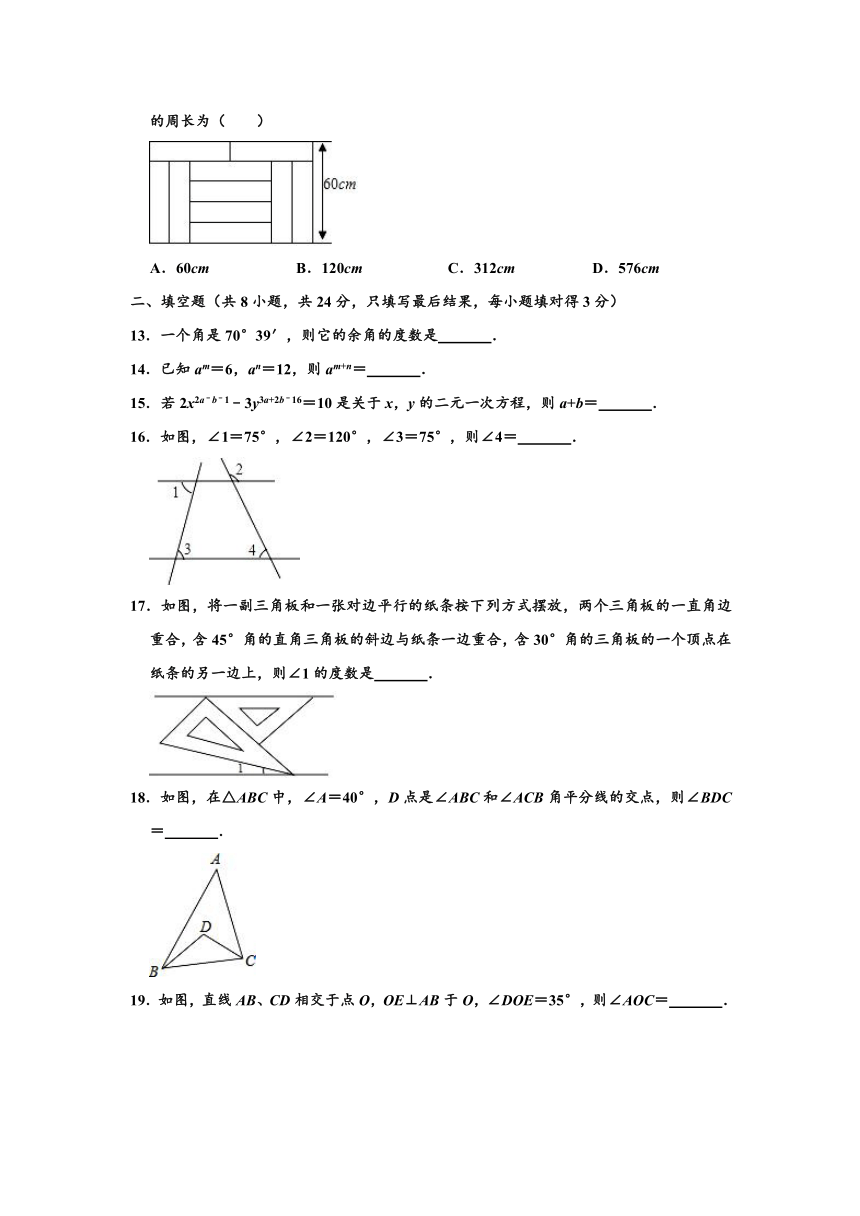
16.如图,∠1=75°,∠2=120°,∠3=75°,则∠4=
.
17.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是
.
18.如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=
.
19.如图,直线AB、CD相交于点O,OE⊥AB于O,∠DOE=35°,则∠AOC=
.
20.已知关于x,y的方程组与方程x+y=3的解相同,则k的值为
.
三、解答题(共7小题,共60分.解答要写出文字说明、证明过程或演算步骤)
21.计算
(1)4a2b(﹣2ab)3
(2)(3+m)(3﹣m)﹣m(m﹣6)﹣7
22.解下列方程组:
(1)
(2)
23.先化简,再求值:(2x﹣1)2﹣x(x+4)+(x﹣2)(x+2),其中x=﹣1.
24.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空).
解:∵EF∥AD
∴∠2=
(
),
又∵∠1=∠2,
∴∠1=∠3(
),
∴AB∥
(
),
∴∠BAC+
=180°(
),
∵∠BAC=70°(
),
∴∠AGD=
(
).
25.若(x2+mx﹣8)(x2﹣3x+n)的展开式中不含x2和x3项,求m和n的值.
26.如图,已知AB∥EF,∠BCD=90°,求∠B+∠D﹣∠E的度数.
27.一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付给两组费用共3480元,问:
(1)甲、乙两组单独工作一天,商店应各付多少元?
(2)已知甲组单独完成需要12天,乙组单独完成需要24天,单独请哪组,商店所付费用较少?
参考答案
一、选择题(共12小题,每小题四个选项只有一项是正确的,每小题选对得3分.)
1.下列图形中,∠1与∠2是对顶角的有( )
A.
B.
C.
D.
【分析】根据对顶角的概念解答即可.
解:A,∠1与∠2是对顶角,A正确;
B,∠1与∠2不是对顶角,B错误;
C,∠1与∠2不是对顶角,C错误;
D,∠1与∠2不是对顶角,D错误;
故选:A.
【点评】本题考查的是对顶角和邻补角的概念和性质,掌握有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角是解题的关键.
2.下列运算正确的是( )
A.a4+a5=a9
B.a3?a3?a3=3a3
C.2a4?3a5=6a9
D.(﹣a3)4=a7
【分析】①同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加;②幂的乘方法则,幂的乘方底数不变指数相乘;
③合并同类项法则,把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变.
解:A、a4+a5=a4+a5,不是同类项不能相加;
B、a3?a3?a3=a9,底数不变,指数相加;
C、正确;
D、(﹣a3)4=a12.底数取正值,指数相乘.
故选:C.
【点评】注意把各种幂运算区别开,从而熟练掌握各种题型的运算.
3.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35°
B.45°
C.55°
D.65°
【分析】由射线OM平分∠AOC,∠AOM=35°,得出∠MOC=35°,由ON⊥OM,得出∠CON=∠MON﹣∠MOC得出答案.
解:∵射线OM平分∠AOC,∠AOM=35°,
∴∠MOC=35°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°.
故选:C.
【点评】本题主要考查了垂线和角平分线,解决本题的关键是找准角的关系.
4.下列命题中是假命题的是( )
A.互补的角不一定是邻补角
B.互补的角若相等,则两个角都是直角
C.一个角的两个邻补角互为对顶角
D.两个锐角的和是锐角
【分析】根据邻补角的概念、补角的定义、对顶角的概念判断.
解:A、互补的角不一定是邻补角,本说法是真命题;
B、互补的角若相等,则两个角都是直角,本说法是真命题;
C、一个角的两个邻补角互为对顶角,本说法是真命题;
D、两个锐角的和是锐角或直角或钝角,本说法是假命题;
故选:D.
【点评】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
5.已知单项式﹣xm﹣2y3与xny2m﹣3n是同类项,那么m,n的值分别是( )
A.
B.
C.
D.
【分析】根据同类项的定义进行选择即可.
解:∵单项式﹣xm﹣2y3与xny2m﹣3n是同类项,
∴m﹣2=n,2m﹣3n=3,
∴m=3,n=1,
故选:B.
【点评】本题考查了同类项,掌握同类项的定义是解题的关键.
6.利用加减消元法解方程组,下列做法正确的是( )
A.将①×5﹣②×2可以消去y
B.将①×3+②×(﹣5)可以消去x
C.将①×5+②×3可以消去y
D.将①×(﹣5)+②×2可以消去x
【分析】利用加减消元法判断即可.
解:利用加减消元法解方程组,将①×(﹣5)+②×2可以消去x,将①×3+②×5可以消去y.
故选:D.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
7.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )
A.①③
B.②④
C.①③④
D.①②③④
【分析】根据平行线的判定方法可以一一证明①、②、③、④都能判断a∥b.
解:∵∠1=∠2,
∴a∥b,故①正确.
∵∠3=∠6,∠3=∠5,
∴∠5=∠6,
∴a∥b,故②正确,
∵∠4+∠7=180°,∠4=∠6,
∴∠6+∠7=180°,
∴a∥b,故③正确,
∵∠5+∠8=180°,∠5=∠3,∠8=∠2,
∴∠2+∠3=180°,
∴a∥b,故④正确,
故选:D.
【点评】本题考查平行线的判定,记住同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,解题的关键是搞清楚同位角、内错角、同旁内角的概念,属于中考常考题型.
8.一个角的两边与另一个角的两边分别平行,那么这两个角( )
A.相等
B.互补
C.相等或互补
D.不能确定
【分析】分两种情况,作出图形,然后解答即可.
解:如图1,两个角相等,
如图2,两个角互补,
所以,一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故选C.
【点评】本题考查了平行线的性质,作出图形,利用数形结合求解更形象直观.
9.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A.90°
B.180°
C.210°
D.270°
【分析】根据两直线平行,同旁内角互补求出∠B+∠C=180°,从而得到以点B、点C为顶点的五边形的两个外角的度数之和等于180°,再根据多边形的外角和定理列式计算即可得解.
解:∵AB∥CD,
∴∠B+∠C=180°,
∴∠4+∠5=180°,
根据多边形的外角和定理,∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故选:B.
【点评】本题考查了平行线的性质,多边形的外角和定理,是基础题,理清求解思路是解题的关键.
10.如图,点D、E分别为三角形ABC边BC、AC上一点,作射线DE,则下列说法错误的是( )
A.∠1与∠3是对顶角
B.∠2与∠A是同位角
C.∠2与∠C是同旁内角
D.∠1与∠4是内错角
【分析】根据同位角、内错角以及同旁内角的概念进行判断.
解:A、∠1与∠3是对顶角,说法正确;
B、∠2与∠A是同位角,说法正确;
C、∠2与∠C是同旁内角,说法正确;
D、∠2与∠4是内错角,说法错误.
故选:D.
【点评】考查了同位角、内错角以及同旁内角,解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
11.若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=﹣6
B.a=5,b=6
C.a=1,b=6
D.a=1,b=﹣6
【分析】已知等式左边利用多项式乘多项式法则计算,再利用多项式相等的条件求出a与b的值即可.
解:已知等式整理得:x2+x﹣6=x2+ax+b,
则a=1,b=﹣6,
故选:D.
【点评】此题考查了多项式乘多项式,以及多项式相等的条件,熟练掌握运算法则是解本题的关键.
12.如图,宽为60cm的矩形图案由10个完全一样的小长方形拼成,则其中一个小长方形的周长为( )
A.60cm
B.120cm
C.312cm
D.576cm
【分析】根据矩形的两组对边分别相等,可知题中有两个等量关系:小长方形的长+小长方形的宽=60,小长方形的长×2=小长方形的长+小长方形的宽×4,根据这两个等量关系,可列出方程组,再求解.
解:设一个小长方形的长为xcm,宽为ycm,
由图形可知,,
解得:.
所以一个小长方形的周长为:2(48+12)=120(cm).
故选:B.
【点评】此题考查了二元一次方程组的应用,解答本题关键是弄清题意,看懂图示,找出合适的等量关系,列出方程组.
二、填空题(共8小题,共24分,只填写最后结果,每小题填对得3分)
13.一个角是70°39′,则它的余角的度数是 19°21′ .
【分析】依据余角的定义列出算式进行计算即可.
解:它的余角=90°﹣70°39′=19°21′.
故答案为:19°21′.
【点评】本题主要考查的是余角的定义以及度分秒的换算,掌握相关概念是解题的关键.
14.已知am=6,an=12,则am+n= 72 .
【分析】根据同底数幂的乘法法则计算即可.
解:∵am=6,an=12,
∴am+n=am?an=6×12=72.
故答案为:72.
【点评】本题主要考查了同底数幂的乘法,同底数幂相乘,底数不变,指数相加.
15.若2x2a﹣b﹣1﹣3y3a+2b﹣16=10是关于x,y的二元一次方程,则a+b= 7 .
【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.则x,y的指数都是1,即可得到一个关于m,n的方程,从而求解.
解:根据题意,得:,
解得:
∴a+b=3+4=7,
故答案为:7.
【点评】主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
16.如图,∠1=75°,∠2=120°,∠3=75°,则∠4= 60° .
【分析】如图,由条件可先证明a∥b,再由平行线的性质可得到∠2=∠5,由邻补角的定义可求得∠4.
解:如图,
∵∠1=75°=∠3,
∴a∥b,
∴∠5=∠2=120°,
∵∠4+∠5=180°,
∴∠4=180°﹣∠5=180°﹣120°=60°,
故答案为:60°.
【点评】本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.
17.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 15° .
【分析】先根据平行线的性质得出∠BCD的度数,进而可得出结论.
解:∵AB∥CD,
∴∠BCD=∠ABC=45°,
∴∠1=∠BCD﹣∠BCE=45°﹣30°=15°.
故答案为:15°.
【点评】本题考查的是等腰直角三角形,平行线的性质,熟知平行线的性质与三角板的特点是解答此题的关键.
18.如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= 110° .
【分析】由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70°,再利用三角形内角和定理即可求出∠BDC的度数.
解:∵D点是∠ABC和∠ACB角平分线的交点,
∴∠CBD=∠ABD=∠ABC,∠BCD=∠ACD=∠ACB,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠DBC+∠DCB=70°,
∴∠BDC=180°﹣70°=110°,
故答案为:110°.
【点评】此题主要考查学生对角平分线性质,三角形内角和定理,熟记三角形内角和定理是解决问题的关键.
19.如图,直线AB、CD相交于点O,OE⊥AB于O,∠DOE=35°,则∠AOC= 55° .
【分析】首先由余角的定义求得∠BOD=55°;然后根据对顶角的定义来求∠AOC的度数.
解:如图,∵OE⊥AB于O,
∴∠BOE=90°.
又∵∠DOE=35°,∠BOD=∠BOE﹣∠DOE,
∴∠BOD=55°,
∴∠AOC=∠BOD=55°.
故答案为:55°.
【点评】本题考查了对顶角相等的性质以及余角的和等于90°的性质,需要熟练掌握.本题考查了对顶角相等的性质以及余角的和等于90°的性质,需要熟练掌握.
20.已知关于x,y的方程组与方程x+y=3的解相同,则k的值为 11 .
【分析】把k看做已知数表示出方程组的解,代入已知方程计算即可求出k的值.
解:,
①×2﹣②得:x=k+5,
把x=k+5代入①得:3k+15+2y=2k,
解得:y=﹣,
代入x+y=3得:k+5﹣=3,
去分母得:2k+10﹣k﹣15=6,
解得:k=11,
故答案为:11
【点评】此题考查了二元一次方程组的解,以及二元一次方程的解,熟练掌握运算法则是解本题的关键.
三、解答题(共7小题,共60分.解答要写出文字说明、证明过程或演算步骤)
21.计算
(1)4a2b(﹣2ab)3
(2)(3+m)(3﹣m)﹣m(m﹣6)﹣7
【分析】(1)原式利用积的乘方运算法则计算,再利用单项式乘单项式法则计算即可求出值;
(2)原式利用平方差公式,单项式乘多项式法则计算,去括号合并即可得到结果.
解:(1)原式=4a2b(﹣8a3b3)
=﹣32a5b4;
(2)原式=9﹣m2﹣m2+6m﹣7
=﹣2m2+6m+2.
【点评】此题考查了整式的混合运算,熟练掌握运算法则及公式是解本题的关键.
22.解下列方程组:
(1)
(2)
【分析】(1)根据代入消元法,可得答案;
(2)根据代入消元法,可得答案.
解:(1),
把①代入②,得
2(y+1)﹣y=3,
解这个方程,得
y=1,
把y=1代入①,得
x=2,
这个方程组的解是;
(2)原方程组化简,得,
把①代入②,得
5x+2(3x﹣5)=23,
解这个方程,得
x=3,
把x=3代入①,得y=4,
原方程组的解是.
【点评】本题考查了解二元一次方程组,利用代入消元法是解题关键.
23.先化简,再求值:(2x﹣1)2﹣x(x+4)+(x﹣2)(x+2),其中x=﹣1.
【分析】先根据整式的乘法法则和乘法公式算乘法,再合并同类项,最后代入求出即可.
解:(2x﹣1)2﹣x(x+4)+(x﹣2)(x+2)
=4x2﹣4x+1﹣x2﹣4x+x2﹣4
=4x2﹣8x﹣3,
当x=﹣1时,
原式=4×(﹣1)2﹣8×(﹣1)﹣3=9.
【点评】本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.
24.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空).
解:∵EF∥AD
∴∠2= ∠3 ( 两直线平行,同位角相等 ),
又∵∠1=∠2,
∴∠1=∠3( 等量代换 ),
∴AB∥ DG ( 内错角相等,两直线平行 ),
∴∠BAC+ ∠DGA =180°( 两直线平行,同旁内角互补 ),
∵∠BAC=70°( 已知 ),
∴∠AGD= 110° ( 等式的性质 ).
【分析】根据平行线的性质和已知求出∠1=∠3,根据平行线的判定推出AB∥DG,根据平行线的性质求出∠BAC+∠DGA=180°即可.
解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),
∵∠BAC=70°(已知),
∴∠AGD=110°(等式的性质).
故答案为:∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠DGA,两直线平行,同旁内角互补,已知,110°,等式的性质.
【点评】本题考查了平行线的性质和判定的应用,能灵活运用平行线的性质和判定定理进行推理是解此题的关键,注意:平行线的性质是①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.
25.若(x2+mx﹣8)(x2﹣3x+n)的展开式中不含x2和x3项,求m和n的值.
【分析】利用多项式乘以多项式法则计算得到结果,根据展开式中不含x2和x3项列出关于m与n的方程组,求出方程组的解即可得到m与n的值.
解:原式=x4+(m﹣3)x3+(n﹣3m﹣8)x2+(mn+24)x﹣8n,
根据展开式中不含x2和x3项得:,
解得:.
【点评】此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.
26.如图,已知AB∥EF,∠BCD=90°,求∠B+∠D﹣∠E的度数.
【分析】过点C作直线CM∥AB,过点D作直线DN∥EF,由AB∥EF可得出CM∥DN,进而可得出∠B=∠1,∠2=∠3,∠4=∠E,根据各角之间的关系可找出∠CDE﹣∠E=∠2,再结合∠BCD=∠1+∠2=90°可得出∠B+∠CDE﹣∠E=90°
解:过点C作直线CM∥AB,过点D作直线DN∥EF,给各角表示序号,如图所示.
∵AB∥EF,CM∥AB,DN∥EF,
∴CM∥DN,
∴∠B=∠1,∠2=∠3,∠4=∠E,
∴∠CDE﹣∠E=∠3+∠4﹣∠E=∠3=∠2,
∴∠B+∠CDE﹣∠E=∠B+∠2=∠1+∠2=∠BCD=90°.
【点评】本题考查了平行线的性质,牢记“两直线平行,内错角相等”是解题的关键.
27.一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付给两组费用共3480元,问:
(1)甲、乙两组单独工作一天,商店应各付多少元?
(2)已知甲组单独完成需要12天,乙组单独完成需要24天,单独请哪组,商店所付费用较少?
【分析】(1)设甲单独工作一天需要x元,乙单独工作一天商店需付y元,根据两组合作8天需付3520元,甲组单独做6天,乙组单独做12天,需付费用共3480元,据此列方程组求解;
(2)求出两组的总费用,然后选择较少的一组.
解:(1)设甲单独工作一天需要x元,乙单独工作一天商店需付y元,
由题意得,,
解得:.
答:甲单独工作一天需要300元,乙单独工作一天商店需付140元;
(2)甲单独完成需付:300×12=3600(元),
乙单独完成需付:140×24=3360(元).
答:选择乙组商店所付费用较少.
【点评】本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.
一、选择题(共12小题)
1.下列图形中,∠1与∠2是对顶角的有( )
A.
B.
C.
D.
2.下列运算正确的是( )
A.a4+a5=a9
B.a3?a3?a3=3a3
C.2a4?3a5=6a9
D.(﹣a3)4=a7
3.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35°
B.45°
C.55°
D.65°
4.下列命题中是假命题的是( )
A.互补的角不一定是邻补角
B.互补的角若相等,则两个角都是直角
C.一个角的两个邻补角互为对顶角
D.两个锐角的和是锐角
5.已知单项式﹣xm﹣2y3与xny2m﹣3n是同类项,那么m,n的值分别是( )
A.
B.
C.
D.
6.利用加减消元法解方程组,下列做法正确的是( )
A.将①×5﹣②×2可以消去y
B.将①×3+②×(﹣5)可以消去x
C.将①×5+②×3可以消去y
D.将①×(﹣5)+②×2可以消去x
7.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )
A.①③
B.②④
C.①③④
D.①②③④
8.一个角的两边与另一个角的两边分别平行,那么这两个角( )
A.相等
B.互补
C.相等或互补
D.不能确定
9.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A.90°
B.180°
C.210°
D.270°
10.如图,点D、E分别为三角形ABC边BC、AC上一点,作射线DE,则下列说法错误的是( )
A.∠1与∠3是对顶角
B.∠2与∠A是同位角
C.∠2与∠C是同旁内角
D.∠1与∠4是内错角
11.若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=﹣6
B.a=5,b=6
C.a=1,b=6
D.a=1,b=﹣6
12.如图,宽为60cm的矩形图案由10个完全一样的小长方形拼成,则其中一个小长方形的周长为( )
A.60cm
B.120cm
C.312cm
D.576cm
二、填空题(共8小题,共24分,只填写最后结果,每小题填对得3分)
13.一个角是70°39′,则它的余角的度数是
.
14.已知am=6,an=12,则am+n=
.
15.若2x2a﹣b﹣1﹣3y3a+2b﹣16=10是关于x,y的二元一次方程,则a+b=
.
16.如图,∠1=75°,∠2=120°,∠3=75°,则∠4=
.
17.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是
.
18.如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=
.
19.如图,直线AB、CD相交于点O,OE⊥AB于O,∠DOE=35°,则∠AOC=
.
20.已知关于x,y的方程组与方程x+y=3的解相同,则k的值为
.
三、解答题(共7小题,共60分.解答要写出文字说明、证明过程或演算步骤)
21.计算
(1)4a2b(﹣2ab)3
(2)(3+m)(3﹣m)﹣m(m﹣6)﹣7
22.解下列方程组:
(1)
(2)
23.先化简,再求值:(2x﹣1)2﹣x(x+4)+(x﹣2)(x+2),其中x=﹣1.
24.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空).
解:∵EF∥AD
∴∠2=
(
),
又∵∠1=∠2,
∴∠1=∠3(
),
∴AB∥
(
),
∴∠BAC+
=180°(
),
∵∠BAC=70°(
),
∴∠AGD=
(
).
25.若(x2+mx﹣8)(x2﹣3x+n)的展开式中不含x2和x3项,求m和n的值.
26.如图,已知AB∥EF,∠BCD=90°,求∠B+∠D﹣∠E的度数.
27.一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付给两组费用共3480元,问:
(1)甲、乙两组单独工作一天,商店应各付多少元?
(2)已知甲组单独完成需要12天,乙组单独完成需要24天,单独请哪组,商店所付费用较少?
参考答案
一、选择题(共12小题,每小题四个选项只有一项是正确的,每小题选对得3分.)
1.下列图形中,∠1与∠2是对顶角的有( )
A.
B.
C.
D.
【分析】根据对顶角的概念解答即可.
解:A,∠1与∠2是对顶角,A正确;
B,∠1与∠2不是对顶角,B错误;
C,∠1与∠2不是对顶角,C错误;
D,∠1与∠2不是对顶角,D错误;
故选:A.
【点评】本题考查的是对顶角和邻补角的概念和性质,掌握有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角是解题的关键.
2.下列运算正确的是( )
A.a4+a5=a9
B.a3?a3?a3=3a3
C.2a4?3a5=6a9
D.(﹣a3)4=a7
【分析】①同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加;②幂的乘方法则,幂的乘方底数不变指数相乘;
③合并同类项法则,把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变.
解:A、a4+a5=a4+a5,不是同类项不能相加;
B、a3?a3?a3=a9,底数不变,指数相加;
C、正确;
D、(﹣a3)4=a12.底数取正值,指数相乘.
故选:C.
【点评】注意把各种幂运算区别开,从而熟练掌握各种题型的运算.
3.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35°
B.45°
C.55°
D.65°
【分析】由射线OM平分∠AOC,∠AOM=35°,得出∠MOC=35°,由ON⊥OM,得出∠CON=∠MON﹣∠MOC得出答案.
解:∵射线OM平分∠AOC,∠AOM=35°,
∴∠MOC=35°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°.
故选:C.
【点评】本题主要考查了垂线和角平分线,解决本题的关键是找准角的关系.
4.下列命题中是假命题的是( )
A.互补的角不一定是邻补角
B.互补的角若相等,则两个角都是直角
C.一个角的两个邻补角互为对顶角
D.两个锐角的和是锐角
【分析】根据邻补角的概念、补角的定义、对顶角的概念判断.
解:A、互补的角不一定是邻补角,本说法是真命题;
B、互补的角若相等,则两个角都是直角,本说法是真命题;
C、一个角的两个邻补角互为对顶角,本说法是真命题;
D、两个锐角的和是锐角或直角或钝角,本说法是假命题;
故选:D.
【点评】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
5.已知单项式﹣xm﹣2y3与xny2m﹣3n是同类项,那么m,n的值分别是( )
A.
B.
C.
D.
【分析】根据同类项的定义进行选择即可.
解:∵单项式﹣xm﹣2y3与xny2m﹣3n是同类项,
∴m﹣2=n,2m﹣3n=3,
∴m=3,n=1,
故选:B.
【点评】本题考查了同类项,掌握同类项的定义是解题的关键.
6.利用加减消元法解方程组,下列做法正确的是( )
A.将①×5﹣②×2可以消去y
B.将①×3+②×(﹣5)可以消去x
C.将①×5+②×3可以消去y
D.将①×(﹣5)+②×2可以消去x
【分析】利用加减消元法判断即可.
解:利用加减消元法解方程组,将①×(﹣5)+②×2可以消去x,将①×3+②×5可以消去y.
故选:D.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
7.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )
A.①③
B.②④
C.①③④
D.①②③④
【分析】根据平行线的判定方法可以一一证明①、②、③、④都能判断a∥b.
解:∵∠1=∠2,
∴a∥b,故①正确.
∵∠3=∠6,∠3=∠5,
∴∠5=∠6,
∴a∥b,故②正确,
∵∠4+∠7=180°,∠4=∠6,
∴∠6+∠7=180°,
∴a∥b,故③正确,
∵∠5+∠8=180°,∠5=∠3,∠8=∠2,
∴∠2+∠3=180°,
∴a∥b,故④正确,
故选:D.
【点评】本题考查平行线的判定,记住同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,解题的关键是搞清楚同位角、内错角、同旁内角的概念,属于中考常考题型.
8.一个角的两边与另一个角的两边分别平行,那么这两个角( )
A.相等
B.互补
C.相等或互补
D.不能确定
【分析】分两种情况,作出图形,然后解答即可.
解:如图1,两个角相等,
如图2,两个角互补,
所以,一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故选C.
【点评】本题考查了平行线的性质,作出图形,利用数形结合求解更形象直观.
9.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A.90°
B.180°
C.210°
D.270°
【分析】根据两直线平行,同旁内角互补求出∠B+∠C=180°,从而得到以点B、点C为顶点的五边形的两个外角的度数之和等于180°,再根据多边形的外角和定理列式计算即可得解.
解:∵AB∥CD,
∴∠B+∠C=180°,
∴∠4+∠5=180°,
根据多边形的外角和定理,∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故选:B.
【点评】本题考查了平行线的性质,多边形的外角和定理,是基础题,理清求解思路是解题的关键.
10.如图,点D、E分别为三角形ABC边BC、AC上一点,作射线DE,则下列说法错误的是( )
A.∠1与∠3是对顶角
B.∠2与∠A是同位角
C.∠2与∠C是同旁内角
D.∠1与∠4是内错角
【分析】根据同位角、内错角以及同旁内角的概念进行判断.
解:A、∠1与∠3是对顶角,说法正确;
B、∠2与∠A是同位角,说法正确;
C、∠2与∠C是同旁内角,说法正确;
D、∠2与∠4是内错角,说法错误.
故选:D.
【点评】考查了同位角、内错角以及同旁内角,解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
11.若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=﹣6
B.a=5,b=6
C.a=1,b=6
D.a=1,b=﹣6
【分析】已知等式左边利用多项式乘多项式法则计算,再利用多项式相等的条件求出a与b的值即可.
解:已知等式整理得:x2+x﹣6=x2+ax+b,
则a=1,b=﹣6,
故选:D.
【点评】此题考查了多项式乘多项式,以及多项式相等的条件,熟练掌握运算法则是解本题的关键.
12.如图,宽为60cm的矩形图案由10个完全一样的小长方形拼成,则其中一个小长方形的周长为( )
A.60cm
B.120cm
C.312cm
D.576cm
【分析】根据矩形的两组对边分别相等,可知题中有两个等量关系:小长方形的长+小长方形的宽=60,小长方形的长×2=小长方形的长+小长方形的宽×4,根据这两个等量关系,可列出方程组,再求解.
解:设一个小长方形的长为xcm,宽为ycm,
由图形可知,,
解得:.
所以一个小长方形的周长为:2(48+12)=120(cm).
故选:B.
【点评】此题考查了二元一次方程组的应用,解答本题关键是弄清题意,看懂图示,找出合适的等量关系,列出方程组.
二、填空题(共8小题,共24分,只填写最后结果,每小题填对得3分)
13.一个角是70°39′,则它的余角的度数是 19°21′ .
【分析】依据余角的定义列出算式进行计算即可.
解:它的余角=90°﹣70°39′=19°21′.
故答案为:19°21′.
【点评】本题主要考查的是余角的定义以及度分秒的换算,掌握相关概念是解题的关键.
14.已知am=6,an=12,则am+n= 72 .
【分析】根据同底数幂的乘法法则计算即可.
解:∵am=6,an=12,
∴am+n=am?an=6×12=72.
故答案为:72.
【点评】本题主要考查了同底数幂的乘法,同底数幂相乘,底数不变,指数相加.
15.若2x2a﹣b﹣1﹣3y3a+2b﹣16=10是关于x,y的二元一次方程,则a+b= 7 .
【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.则x,y的指数都是1,即可得到一个关于m,n的方程,从而求解.
解:根据题意,得:,
解得:
∴a+b=3+4=7,
故答案为:7.
【点评】主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
16.如图,∠1=75°,∠2=120°,∠3=75°,则∠4= 60° .
【分析】如图,由条件可先证明a∥b,再由平行线的性质可得到∠2=∠5,由邻补角的定义可求得∠4.
解:如图,
∵∠1=75°=∠3,
∴a∥b,
∴∠5=∠2=120°,
∵∠4+∠5=180°,
∴∠4=180°﹣∠5=180°﹣120°=60°,
故答案为:60°.
【点评】本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.
17.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 15° .
【分析】先根据平行线的性质得出∠BCD的度数,进而可得出结论.
解:∵AB∥CD,
∴∠BCD=∠ABC=45°,
∴∠1=∠BCD﹣∠BCE=45°﹣30°=15°.
故答案为:15°.
【点评】本题考查的是等腰直角三角形,平行线的性质,熟知平行线的性质与三角板的特点是解答此题的关键.
18.如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= 110° .
【分析】由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70°,再利用三角形内角和定理即可求出∠BDC的度数.
解:∵D点是∠ABC和∠ACB角平分线的交点,
∴∠CBD=∠ABD=∠ABC,∠BCD=∠ACD=∠ACB,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠DBC+∠DCB=70°,
∴∠BDC=180°﹣70°=110°,
故答案为:110°.
【点评】此题主要考查学生对角平分线性质,三角形内角和定理,熟记三角形内角和定理是解决问题的关键.
19.如图,直线AB、CD相交于点O,OE⊥AB于O,∠DOE=35°,则∠AOC= 55° .
【分析】首先由余角的定义求得∠BOD=55°;然后根据对顶角的定义来求∠AOC的度数.
解:如图,∵OE⊥AB于O,
∴∠BOE=90°.
又∵∠DOE=35°,∠BOD=∠BOE﹣∠DOE,
∴∠BOD=55°,
∴∠AOC=∠BOD=55°.
故答案为:55°.
【点评】本题考查了对顶角相等的性质以及余角的和等于90°的性质,需要熟练掌握.本题考查了对顶角相等的性质以及余角的和等于90°的性质,需要熟练掌握.
20.已知关于x,y的方程组与方程x+y=3的解相同,则k的值为 11 .
【分析】把k看做已知数表示出方程组的解,代入已知方程计算即可求出k的值.
解:,
①×2﹣②得:x=k+5,
把x=k+5代入①得:3k+15+2y=2k,
解得:y=﹣,
代入x+y=3得:k+5﹣=3,
去分母得:2k+10﹣k﹣15=6,
解得:k=11,
故答案为:11
【点评】此题考查了二元一次方程组的解,以及二元一次方程的解,熟练掌握运算法则是解本题的关键.
三、解答题(共7小题,共60分.解答要写出文字说明、证明过程或演算步骤)
21.计算
(1)4a2b(﹣2ab)3
(2)(3+m)(3﹣m)﹣m(m﹣6)﹣7
【分析】(1)原式利用积的乘方运算法则计算,再利用单项式乘单项式法则计算即可求出值;
(2)原式利用平方差公式,单项式乘多项式法则计算,去括号合并即可得到结果.
解:(1)原式=4a2b(﹣8a3b3)
=﹣32a5b4;
(2)原式=9﹣m2﹣m2+6m﹣7
=﹣2m2+6m+2.
【点评】此题考查了整式的混合运算,熟练掌握运算法则及公式是解本题的关键.
22.解下列方程组:
(1)
(2)
【分析】(1)根据代入消元法,可得答案;
(2)根据代入消元法,可得答案.
解:(1),
把①代入②,得
2(y+1)﹣y=3,
解这个方程,得
y=1,
把y=1代入①,得
x=2,
这个方程组的解是;
(2)原方程组化简,得,
把①代入②,得
5x+2(3x﹣5)=23,
解这个方程,得
x=3,
把x=3代入①,得y=4,
原方程组的解是.
【点评】本题考查了解二元一次方程组,利用代入消元法是解题关键.
23.先化简,再求值:(2x﹣1)2﹣x(x+4)+(x﹣2)(x+2),其中x=﹣1.
【分析】先根据整式的乘法法则和乘法公式算乘法,再合并同类项,最后代入求出即可.
解:(2x﹣1)2﹣x(x+4)+(x﹣2)(x+2)
=4x2﹣4x+1﹣x2﹣4x+x2﹣4
=4x2﹣8x﹣3,
当x=﹣1时,
原式=4×(﹣1)2﹣8×(﹣1)﹣3=9.
【点评】本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.
24.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空).
解:∵EF∥AD
∴∠2= ∠3 ( 两直线平行,同位角相等 ),
又∵∠1=∠2,
∴∠1=∠3( 等量代换 ),
∴AB∥ DG ( 内错角相等,两直线平行 ),
∴∠BAC+ ∠DGA =180°( 两直线平行,同旁内角互补 ),
∵∠BAC=70°( 已知 ),
∴∠AGD= 110° ( 等式的性质 ).
【分析】根据平行线的性质和已知求出∠1=∠3,根据平行线的判定推出AB∥DG,根据平行线的性质求出∠BAC+∠DGA=180°即可.
解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),
∵∠BAC=70°(已知),
∴∠AGD=110°(等式的性质).
故答案为:∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠DGA,两直线平行,同旁内角互补,已知,110°,等式的性质.
【点评】本题考查了平行线的性质和判定的应用,能灵活运用平行线的性质和判定定理进行推理是解此题的关键,注意:平行线的性质是①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.
25.若(x2+mx﹣8)(x2﹣3x+n)的展开式中不含x2和x3项,求m和n的值.
【分析】利用多项式乘以多项式法则计算得到结果,根据展开式中不含x2和x3项列出关于m与n的方程组,求出方程组的解即可得到m与n的值.
解:原式=x4+(m﹣3)x3+(n﹣3m﹣8)x2+(mn+24)x﹣8n,
根据展开式中不含x2和x3项得:,
解得:.
【点评】此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.
26.如图,已知AB∥EF,∠BCD=90°,求∠B+∠D﹣∠E的度数.
【分析】过点C作直线CM∥AB,过点D作直线DN∥EF,由AB∥EF可得出CM∥DN,进而可得出∠B=∠1,∠2=∠3,∠4=∠E,根据各角之间的关系可找出∠CDE﹣∠E=∠2,再结合∠BCD=∠1+∠2=90°可得出∠B+∠CDE﹣∠E=90°
解:过点C作直线CM∥AB,过点D作直线DN∥EF,给各角表示序号,如图所示.
∵AB∥EF,CM∥AB,DN∥EF,
∴CM∥DN,
∴∠B=∠1,∠2=∠3,∠4=∠E,
∴∠CDE﹣∠E=∠3+∠4﹣∠E=∠3=∠2,
∴∠B+∠CDE﹣∠E=∠B+∠2=∠1+∠2=∠BCD=90°.
【点评】本题考查了平行线的性质,牢记“两直线平行,内错角相等”是解题的关键.
27.一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付给两组费用共3480元,问:
(1)甲、乙两组单独工作一天,商店应各付多少元?
(2)已知甲组单独完成需要12天,乙组单独完成需要24天,单独请哪组,商店所付费用较少?
【分析】(1)设甲单独工作一天需要x元,乙单独工作一天商店需付y元,根据两组合作8天需付3520元,甲组单独做6天,乙组单独做12天,需付费用共3480元,据此列方程组求解;
(2)求出两组的总费用,然后选择较少的一组.
解:(1)设甲单独工作一天需要x元,乙单独工作一天商店需付y元,
由题意得,,
解得:.
答:甲单独工作一天需要300元,乙单独工作一天商店需付140元;
(2)甲单独完成需付:300×12=3600(元),
乙单独完成需付:140×24=3360(元).
答:选择乙组商店所付费用较少.
【点评】本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.
同课章节目录
