人教版初中数学七年级下册第六章实数复习课件(共22张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册第六章实数复习课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 10:00:20 | ||
图片预览







文档简介
(共22张PPT)
第六章
实数
(复习)
学习目标
1、理解平方根、算术平方根、立方根、无理数和实数的概念,知道实数与数轴上的点一一对应。
2、会用根号表示数的平方根、算术平方根、立方根,会用平方运算求非负数的平方根和算术平方根,会用立方运算求一个数的立方根,能进行有关实数的简单四则运算。
3、能用有理数估计一个无理数的大致范围,能按问题的要求对结果取近似值。
学习重点
(1)平方根、算术平方根、立方根、无理数和实数的概念;
(2)实数的简单四则运算。
学习难点
(1)平方根和立方根的概念;
(2)实数的简单四则运算。
知识梳理,把握重点
算术平方根的概念是什么?
平方根的概念是什么?这两个概念的区别与联系是什么?
什么叫做开平方?
平方根的性质是什么?
定义
一般地,如果一个正数
x
的平方等于
a(x2
=
a),那么这个正数
x
就叫做
a
的
算术平方根
a
的算术平方根记作
读作
“
根号a
”
根号
被开方数
规定:0的算术平方根等于0
如102
=
100
则100的算术平方根
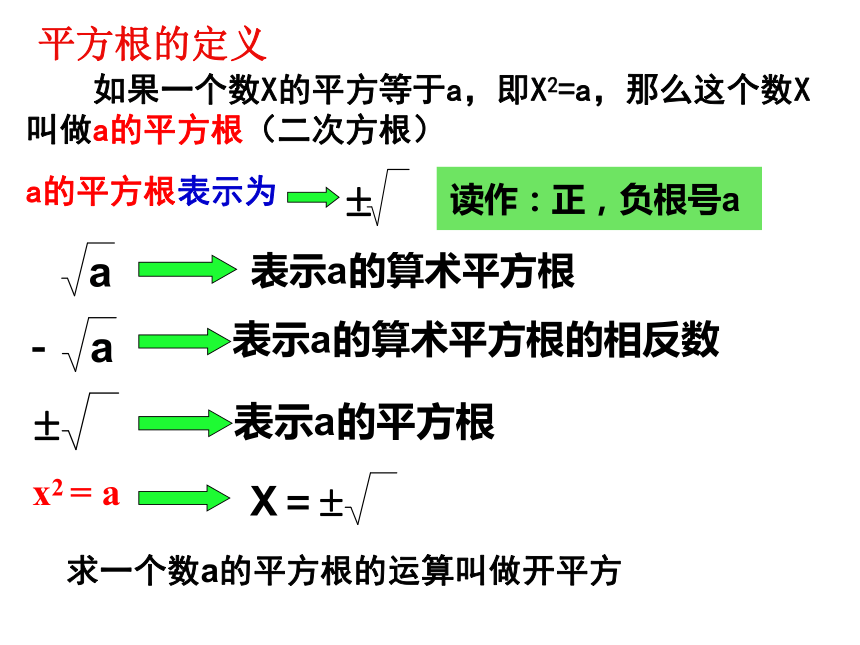
如果一个数X的平方等于a,即X2=a,那么这个数X叫做a的平方根(二次方根)
a的平方根表示为
x2
=
a
求一个数a的平方根的运算叫做开平方
平方根的定义
平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
立方根的概念是什么?
立方根的性质是什么?
平方根和立方根的有什么异同点?
算术平方根、平方根、立方根联系和
区别是什么?
知识梳理,把握重点
若一个数的立方等于a,那么这个数叫做
a
的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0
的立方根是____;立方根是它本身的数是______.平方根是它本身的数是__算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
?
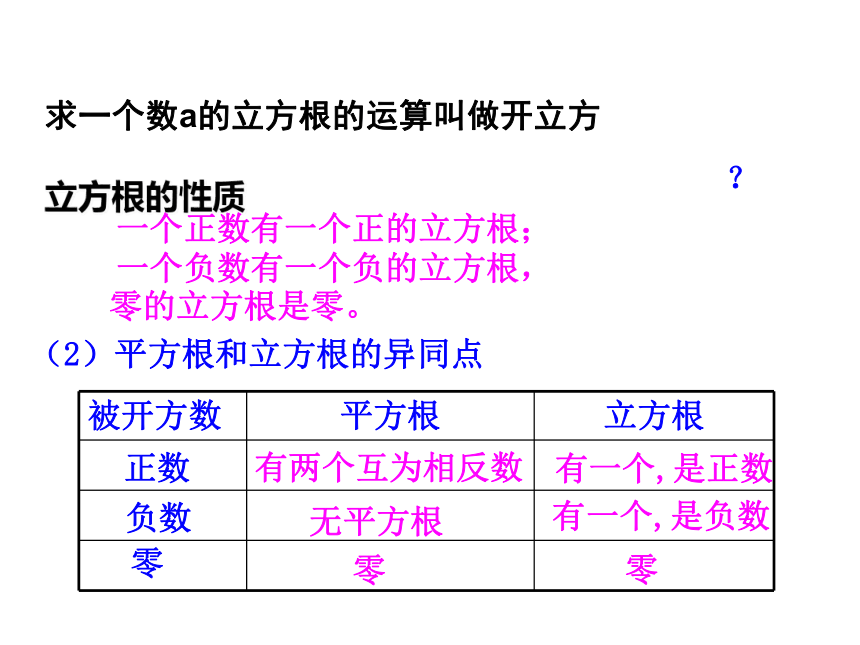
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
求一个数a的立方根的运算叫做开立方
立方根的性质
(2)平方根和立方根的异同点
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
被开方数
平方根
立方根
你知道算术平方根、平方根、立方根联系和区别吗?
表示方法
性
质
开方
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
算术平方根
平方根
立方根
无限不循环的小数
叫做无理数.
在进行实数的运算时,有理数的运算法则及运算性质同样适用。
有理数和无理数统称实数.
实数与
上的点是一一对应的
在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样
数轴
无理数和有理数的区别是什么?
知识梳理,把握重点
无理数不能表示成两个整数之比,
是无限不循环小数.
有理数是能够表示成两个整数之比的数,是整数或有限小数及无限循环小数.
实数
有理数
无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
=
重要公式
典型分析,强调方法
例1 求下列各数的算术平方根及平方根:
(1)64;
(2)0.25;
(3)
.
典型分析,强调方法
例2
求下列各数的立方根:
典型分析,强调方法
例3 下列各数分别介于哪两个相邻的整数之间:
典型分析,强调方法
例4 比较下列各组数的大小:
典型分析,强调方法
例5 计算下列各式的值:
典型分析,强调方法
例6 下列各数:
答案:①②⑤⑥;③④⑦.
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
1.如果一个数的平方根为a+1和2a-7,
求这个数
3.已知y=
求2(x+y)的平方根
4.已知5+
的小数部分为
m,
7-
的小数部分为n,求m+n的值
5.已知满足
,求a的值
2.已知等腰三角形两边长a,b满足
求此等腰三角形的周长
练习
第六章
实数
(复习)
学习目标
1、理解平方根、算术平方根、立方根、无理数和实数的概念,知道实数与数轴上的点一一对应。
2、会用根号表示数的平方根、算术平方根、立方根,会用平方运算求非负数的平方根和算术平方根,会用立方运算求一个数的立方根,能进行有关实数的简单四则运算。
3、能用有理数估计一个无理数的大致范围,能按问题的要求对结果取近似值。
学习重点
(1)平方根、算术平方根、立方根、无理数和实数的概念;
(2)实数的简单四则运算。
学习难点
(1)平方根和立方根的概念;
(2)实数的简单四则运算。
知识梳理,把握重点
算术平方根的概念是什么?
平方根的概念是什么?这两个概念的区别与联系是什么?
什么叫做开平方?
平方根的性质是什么?
定义
一般地,如果一个正数
x
的平方等于
a(x2
=
a),那么这个正数
x
就叫做
a
的
算术平方根
a
的算术平方根记作
读作
“
根号a
”
根号
被开方数
规定:0的算术平方根等于0
如102
=
100
则100的算术平方根
如果一个数X的平方等于a,即X2=a,那么这个数X叫做a的平方根(二次方根)
a的平方根表示为
x2
=
a
求一个数a的平方根的运算叫做开平方
平方根的定义
平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
立方根的概念是什么?
立方根的性质是什么?
平方根和立方根的有什么异同点?
算术平方根、平方根、立方根联系和
区别是什么?
知识梳理,把握重点
若一个数的立方等于a,那么这个数叫做
a
的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0
的立方根是____;立方根是它本身的数是______.平方根是它本身的数是__算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
求一个数a的立方根的运算叫做开立方
立方根的性质
(2)平方根和立方根的异同点
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
被开方数
平方根
立方根
你知道算术平方根、平方根、立方根联系和区别吗?
表示方法
性
质
开方
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
算术平方根
平方根
立方根
无限不循环的小数
叫做无理数.
在进行实数的运算时,有理数的运算法则及运算性质同样适用。
有理数和无理数统称实数.
实数与
上的点是一一对应的
在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样
数轴
无理数和有理数的区别是什么?
知识梳理,把握重点
无理数不能表示成两个整数之比,
是无限不循环小数.
有理数是能够表示成两个整数之比的数,是整数或有限小数及无限循环小数.
实数
有理数
无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
=
重要公式
典型分析,强调方法
例1 求下列各数的算术平方根及平方根:
(1)64;
(2)0.25;
(3)
.
典型分析,强调方法
例2
求下列各数的立方根:
典型分析,强调方法
例3 下列各数分别介于哪两个相邻的整数之间:
典型分析,强调方法
例4 比较下列各组数的大小:
典型分析,强调方法
例5 计算下列各式的值:
典型分析,强调方法
例6 下列各数:
答案:①②⑤⑥;③④⑦.
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
1.如果一个数的平方根为a+1和2a-7,
求这个数
3.已知y=
求2(x+y)的平方根
4.已知5+
的小数部分为
m,
7-
的小数部分为n,求m+n的值
5.已知满足
,求a的值
2.已知等腰三角形两边长a,b满足
求此等腰三角形的周长
练习
