人教版七年级数学下册课件:9.1.2 不等式的性质(37张ppt)
文档属性
| 名称 | 人教版七年级数学下册课件:9.1.2 不等式的性质(37张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 11:20:57 | ||
图片预览








文档简介
(共37张PPT)
9.1.2
不等式的性质
9
不等式与不等式组
课时目标
1.掌握不等式的三条基本性质并且能正确地运用基本性质并且能正确地运用基本性质来解不等式。
2.经历合作探究不等式基本性质的过程,体会不等式与等式的异同点。培养类比的数学思想方法。
复习引入
我们已经学习过等式的基本性质
猜想
:不等式也具有同样的性质吗?
等式的两边都乘以(或除以)一个不为0的数,等式仍然成立.
等式的两边都加上(或都减去)同一个数或同一个整式,
等式仍然成立.
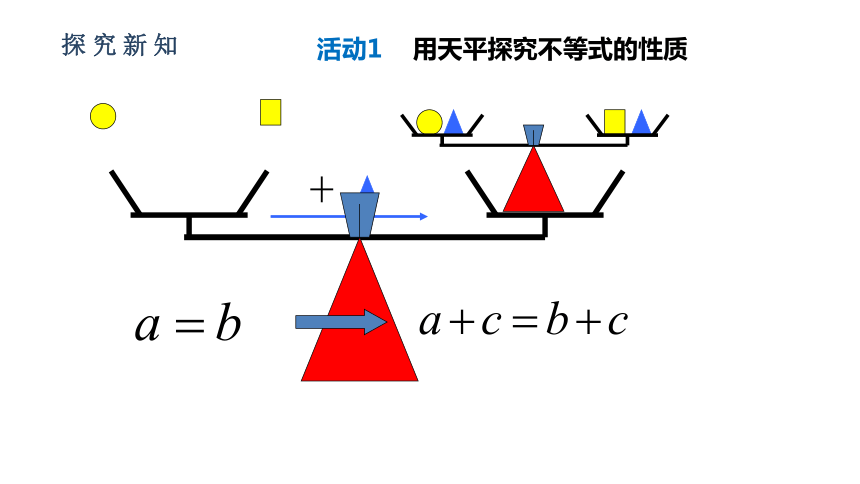
探究新知
+
活动1
用天平探究不等式的性质
探究新知
解:因为
a>b,两边都加上3,
因为
a由不等式基本性质1,得
a+3
>
b+3;
由不等式基本性质1,得
a-5
<
b-5
.
(1)已知
a>b,则a+3
b+3
(2)已知
ab-5
>
<
例1
用“>”或“<”填空:
探究新知
(1)若x+3>6,则x______3,根据______________;
(2)若a-2<3,则a______5,根据____________.
>
<
不等式性质1
不等式性质1
用“>”或“<”填空,并说明是根据不等式的哪一条性质:
探究新知
不等式的基本性质2、3
问题1
已知苹果的价格是a元/kg,梨的价格是b元/kg,且a
>
b.
小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空:
3a
3b.
问题2
在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b.
已知每队人员均为3名,则哪队的平均得分高?
用不等号填空:
a÷3
b÷3.
>
>
探究新知
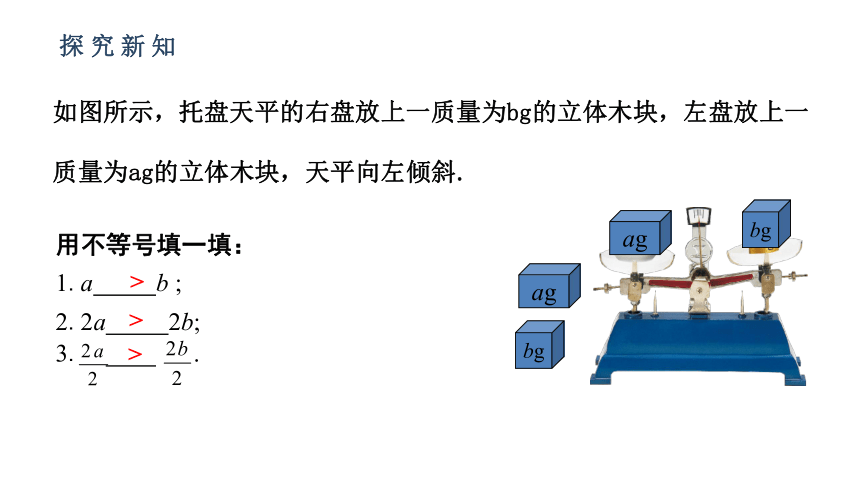
用不等号填一填:
1.a
b
;
2.2a
2b;
3.
.
如图所示,托盘天平的右盘放上一质量为bg的立体木块,左盘放上一质量为ag的立体木块,天平向左倾斜.
ag
bg
>
>
>
ag
bg
探究新知
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即,如果a
>
b,c
>
0,那么
ac
>
bc
,
>
.
不等式基本性质2
探究新知
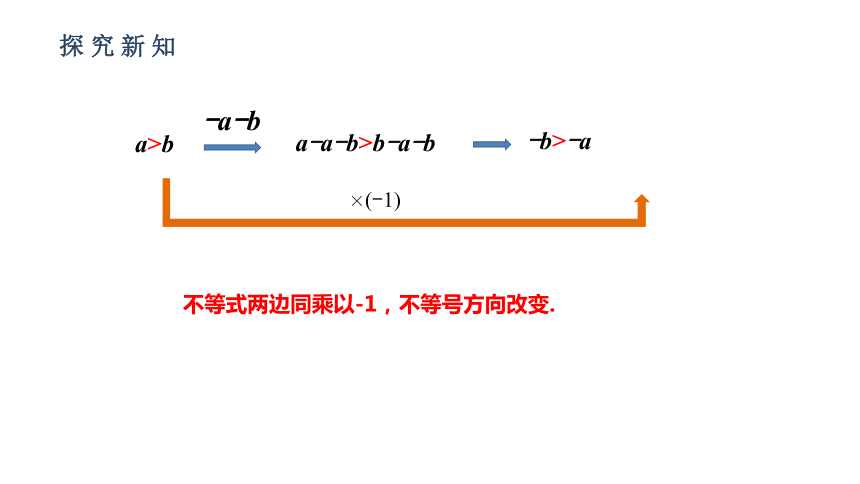
a>b
-a-b
a-a-b>b-a-b
-b>-a
×(-1)
不等式两边同乘以-1,不等号方向改变.
探究新知
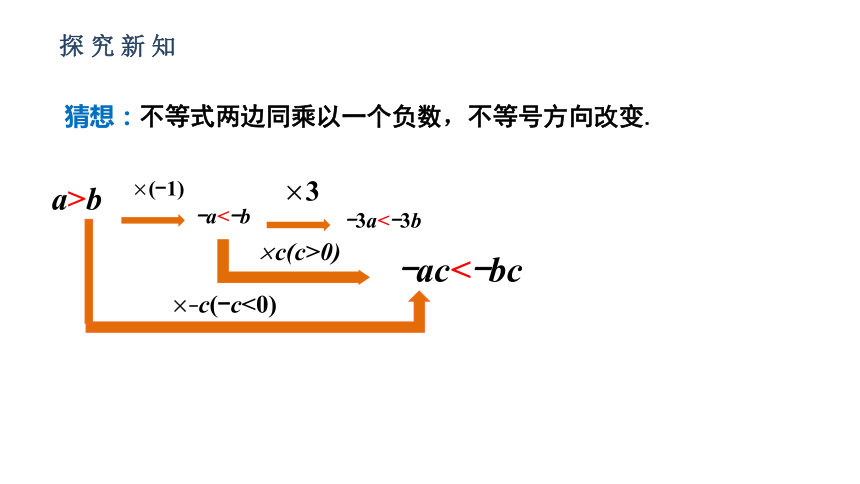
a>b
×(-1)
-a<-b
×3
-3a<-3b
×c(c>0)
-ac<-bc
×-c(-c<0)
猜想:不等式两边同乘以一个负数,不等号方向改变.
探究新知
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a
>
b,c
<
0,那么
ac
<
bc
,
<
.
不等式基本性质3
探究新知
因为
a>b,两边都乘3,由不等式基本性质2,得3a
>
3b.
因为
a>b,两边都乘-1,
解:
由不等式基本性质3,得由不等式基本性质2,得3a
>
3b.
(1)已知
a>b,则3a
3b
;
(2)已知
a>b,则-a
-b
.
>
<
例2
用“>”或“<”填空:
解:
探究新知
因为
a由不等式基本性质1,得
(3)已知
a.
>
因为
,两边都加上2,
探究新知
例1
设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1)
a
-
7____b
-
7;
(2)
a÷6____b÷6
(3)
0.1a____0.1b;
>
>
>
不等式的性质1
不等式的性质2
不等式的性质2
探究新知
(4)
-4a____-4b
(5)
2a+3____2b+3;
(6)(m2+1)a____
(m2+1)b(m为常数)
>
>
<
不等式的性质3
不等式的性质1,2
不等式的性质2
巩固练习
例2
已知a<0,用“<”“>”填空:
(1)a+2
____2;
?(2)a-1
_____-1;
(3)3a______0;
(4)
______0;
(5)a2_____0;
(6)a3______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
巩固练习
思考:
等式有对称性及传递性,那么不等式具有对称性和传递性吗?已知x>5,那么5由8如:8<10,10<15
,8
15.
x>5
5<
性质4(对称性):如果a>b,那么b性质5(同向传递性):如果a>b,b>c,那么a>c.
巩固练习
例3
如果不等式
(a+1)x<a+1可变形为
x>1,那么a
必须满足________.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得
a<-1.
a<-1
方法总结:
只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
巩固练习
例4
利用不等式的性质解下列不等式:
(1)
x-7>26;
(2)
3x<2x+1;
(3)
>50;
(4)
-4x>3.
解未知数为x的不等式
化为x
>a
或x﹤a
的形式
目标
方法:不等式基本性质1~3
利用不等式的性质解简单的不等式
思路:
巩固练习
解:
(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1)
x-7>26;
巩固练习
(2)为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等号的方向_____,得
.
3x-2x﹤2x+1-2x
,即
x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
(2)
3x<2x+1;
巩固练习
(3)为了使不等式
﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以
,不等号的方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
(3)
>50;
(4)为了使不等式-4x﹥3中的不等号的一边变为x,根据______________,不等式两边都除以____,不等号的方向______,得
x﹤-
.
巩固练习
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
(4)
-4x>3
巩固练习
1.已知a
<
b,用“>”或“<”填空:
(1)a
+12
b
+12
;
(2)b-10
a
-10
.
<
>
解:x
<
2
解:x
<
6
2.
把下列不等式化为x>a或x(1)5>3+x;
(2)2x<x+6.
练一练
巩固练习
3.利用不等式的性质解下列不等式,并在数轴上表示其解集.
(2)-2x
>
3
(1)x-5
>
-1
(3)7x
<
6x-6
x>4
x<-6
4
0
0
0
-6
巩固练习
问题1
一辆轿车在一条规定车速不低于60km/h,且不高于100
km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?
含“≤”“≥”的不等式
根据路程与速度、时间之间的关系可得:s≥60x,且s≤100x.
巩固练习
问题2
铁路部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160cm.设行李的长、宽、高分别为acm,bcm,ccm,请你列出行李的长、宽、高满足的关系式.
根据题意可得:
a+b+c≤160.
巩固练习
我们把用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.其中“≥”读作大于等于,“≤”读作小于等于.
不等式的概念
巩固练习
例1
某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V
(单位:cm3)表示新注入水的体积,写出V的取值范围.
巩固练习
解:新注入水的体积V与原有水的体积的和不能超过容器的容积,即
V+3×5×3≤3×5×10
解得
V≤105
又由于新注入水的体积不能是负数,因此,V
的取值范围是V≥0并且V≤105.
在数轴上表示V
的取值范围如图
0
105
在表示0和105的点上画实心圆点,表示取值范围包括这两个数
巩固练习
2.要注意区分“大于”
“不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来.
3.在数轴上表示解集应注意的问题:方向、空心圆圈或实心圆点.
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
利用不等式的性质解不等式的注意事项
巩固练习
用不等式表示下列语句并写出解集,并在数轴上表示解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
分析:准确找出本题中表示数量不等关系的关键词语,并正确使用不等号.(1)(2)中大于或等于、不小于都用“
≥”表示;(3)(4)中不大于、小于或等于都用“≤”表示.
(4)y的
小于或等于-2.
巩固练习
0
0
3
0
1
0
-8
解:(1)3x≥1,
解集是x≥
;
(2)x+3≥6,
解集是x≥3;
(3)y-1≤0,
解集是y≤1;
(4)
y≤-2,
解集是y≤-8.
巩固练习
小希就读的学校上午第一节课的上课时间是8点.小希家距学校有2千米,而她的步行速度为每小时10千米.那么,小希上午几点从家里出发才能保证不迟到?
解:设小希上午x点从家里出发才能不迟到,根据题意得
答:小希上午7:48前从家里出发才能不迟到.
≤8
解得x≤
不等式的性质1
不等式两边加(或减)同一个数(或式子),不等号的方向不变。
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变。
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变。
课堂小结
符号“≥”读作“大于或等于”,也可说是“不小于”;
符号“≤”读作“小于或等于”,也可说是“不大于”。
a≥b或a≤b形式的式子,具有与前面所说的不等式的性质类似的性质。
解不等式时可根据不等式的性质逐步把不等式转化为x>a或x课堂小结
9.1.2
不等式的性质
9
不等式与不等式组
课时目标
1.掌握不等式的三条基本性质并且能正确地运用基本性质并且能正确地运用基本性质来解不等式。
2.经历合作探究不等式基本性质的过程,体会不等式与等式的异同点。培养类比的数学思想方法。
复习引入
我们已经学习过等式的基本性质
猜想
:不等式也具有同样的性质吗?
等式的两边都乘以(或除以)一个不为0的数,等式仍然成立.
等式的两边都加上(或都减去)同一个数或同一个整式,
等式仍然成立.
探究新知
+
活动1
用天平探究不等式的性质
探究新知
解:因为
a>b,两边都加上3,
因为
a
a+3
>
b+3;
由不等式基本性质1,得
a-5
<
b-5
.
(1)已知
a>b,则a+3
b+3
(2)已知
a
>
<
例1
用“>”或“<”填空:
探究新知
(1)若x+3>6,则x______3,根据______________;
(2)若a-2<3,则a______5,根据____________.
>
<
不等式性质1
不等式性质1
用“>”或“<”填空,并说明是根据不等式的哪一条性质:
探究新知
不等式的基本性质2、3
问题1
已知苹果的价格是a元/kg,梨的价格是b元/kg,且a
>
b.
小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空:
3a
3b.
问题2
在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b.
已知每队人员均为3名,则哪队的平均得分高?
用不等号填空:
a÷3
b÷3.
>
>
探究新知
用不等号填一填:
1.a
b
;
2.2a
2b;
3.
.
如图所示,托盘天平的右盘放上一质量为bg的立体木块,左盘放上一质量为ag的立体木块,天平向左倾斜.
ag
bg
>
>
>
ag
bg
探究新知
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即,如果a
>
b,c
>
0,那么
ac
>
bc
,
>
.
不等式基本性质2
探究新知
a>b
-a-b
a-a-b>b-a-b
-b>-a
×(-1)
不等式两边同乘以-1,不等号方向改变.
探究新知
a>b
×(-1)
-a<-b
×3
-3a<-3b
×c(c>0)
-ac<-bc
×-c(-c<0)
猜想:不等式两边同乘以一个负数,不等号方向改变.
探究新知
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a
>
b,c
<
0,那么
ac
<
bc
,
<
.
不等式基本性质3
探究新知
因为
a>b,两边都乘3,由不等式基本性质2,得3a
>
3b.
因为
a>b,两边都乘-1,
解:
由不等式基本性质3,得由不等式基本性质2,得3a
>
3b.
(1)已知
a>b,则3a
3b
;
(2)已知
a>b,则-a
-b
.
>
<
例2
用“>”或“<”填空:
解:
探究新知
因为
a
(3)已知
a
>
因为
,两边都加上2,
探究新知
例1
设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1)
a
-
7____b
-
7;
(2)
a÷6____b÷6
(3)
0.1a____0.1b;
>
>
>
不等式的性质1
不等式的性质2
不等式的性质2
探究新知
(4)
-4a____-4b
(5)
2a+3____2b+3;
(6)(m2+1)a____
(m2+1)b(m为常数)
>
>
<
不等式的性质3
不等式的性质1,2
不等式的性质2
巩固练习
例2
已知a<0,用“<”“>”填空:
(1)a+2
____2;
?(2)a-1
_____-1;
(3)3a______0;
(4)
______0;
(5)a2_____0;
(6)a3______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
巩固练习
思考:
等式有对称性及传递性,那么不等式具有对称性和传递性吗?已知x>5,那么5
,8
15.
x>5
5
性质4(对称性):如果a>b,那么b
巩固练习
例3
如果不等式
(a+1)x<a+1可变形为
x>1,那么a
必须满足________.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得
a<-1.
a<-1
方法总结:
只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
巩固练习
例4
利用不等式的性质解下列不等式:
(1)
x-7>26;
(2)
3x<2x+1;
(3)
>50;
(4)
-4x>3.
解未知数为x的不等式
化为x
>a
或x﹤a
的形式
目标
方法:不等式基本性质1~3
利用不等式的性质解简单的不等式
思路:
巩固练习
解:
(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1)
x-7>26;
巩固练习
(2)为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等号的方向_____,得
.
3x-2x﹤2x+1-2x
,即
x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
(2)
3x<2x+1;
巩固练习
(3)为了使不等式
﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以
,不等号的方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
(3)
>50;
(4)为了使不等式-4x﹥3中的不等号的一边变为x,根据______________,不等式两边都除以____,不等号的方向______,得
x﹤-
.
巩固练习
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
(4)
-4x>3
巩固练习
1.已知a
<
b,用“>”或“<”填空:
(1)a
+12
b
+12
;
(2)b-10
a
-10
.
<
>
解:x
<
2
解:x
<
6
2.
把下列不等式化为x>a或x
(2)2x<x+6.
练一练
巩固练习
3.利用不等式的性质解下列不等式,并在数轴上表示其解集.
(2)-2x
>
3
(1)x-5
>
-1
(3)7x
<
6x-6
x>4
x<-6
4
0
0
0
-6
巩固练习
问题1
一辆轿车在一条规定车速不低于60km/h,且不高于100
km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?
含“≤”“≥”的不等式
根据路程与速度、时间之间的关系可得:s≥60x,且s≤100x.
巩固练习
问题2
铁路部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160cm.设行李的长、宽、高分别为acm,bcm,ccm,请你列出行李的长、宽、高满足的关系式.
根据题意可得:
a+b+c≤160.
巩固练习
我们把用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.其中“≥”读作大于等于,“≤”读作小于等于.
不等式的概念
巩固练习
例1
某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V
(单位:cm3)表示新注入水的体积,写出V的取值范围.
巩固练习
解:新注入水的体积V与原有水的体积的和不能超过容器的容积,即
V+3×5×3≤3×5×10
解得
V≤105
又由于新注入水的体积不能是负数,因此,V
的取值范围是V≥0并且V≤105.
在数轴上表示V
的取值范围如图
0
105
在表示0和105的点上画实心圆点,表示取值范围包括这两个数
巩固练习
2.要注意区分“大于”
“不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来.
3.在数轴上表示解集应注意的问题:方向、空心圆圈或实心圆点.
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
利用不等式的性质解不等式的注意事项
巩固练习
用不等式表示下列语句并写出解集,并在数轴上表示解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
分析:准确找出本题中表示数量不等关系的关键词语,并正确使用不等号.(1)(2)中大于或等于、不小于都用“
≥”表示;(3)(4)中不大于、小于或等于都用“≤”表示.
(4)y的
小于或等于-2.
巩固练习
0
0
3
0
1
0
-8
解:(1)3x≥1,
解集是x≥
;
(2)x+3≥6,
解集是x≥3;
(3)y-1≤0,
解集是y≤1;
(4)
y≤-2,
解集是y≤-8.
巩固练习
小希就读的学校上午第一节课的上课时间是8点.小希家距学校有2千米,而她的步行速度为每小时10千米.那么,小希上午几点从家里出发才能保证不迟到?
解:设小希上午x点从家里出发才能不迟到,根据题意得
答:小希上午7:48前从家里出发才能不迟到.
≤8
解得x≤
不等式的性质1
不等式两边加(或减)同一个数(或式子),不等号的方向不变。
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变。
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变。
课堂小结
符号“≥”读作“大于或等于”,也可说是“不小于”;
符号“≤”读作“小于或等于”,也可说是“不大于”。
a≥b或a≤b形式的式子,具有与前面所说的不等式的性质类似的性质。
解不等式时可根据不等式的性质逐步把不等式转化为x>a或x
