2020-2021北师大版七年级数学上册第六章-数据的收集与整理单元检测题含解析
文档属性
| 名称 | 2020-2021北师大版七年级数学上册第六章-数据的收集与整理单元检测题含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 12:41:29 | ||
图片预览


文档简介
2020-2021北师大版七年级数学上册第六章-数据的收集与整理
一、单选题
1.下列调查中,适合采用全面调查(普查)方式的是( )?????
A.?对某班50名同学视力情况的调查?????????????
B.?对元宵节期间市场上汤圆质量情况的调查
C.?对某类烟花爆竹燃放质量情况的调查??????????????????
D.?对重庆嘉陵江水质情况的调查
2.下列事件:①调查长江现有鱼的数量;②学校为七年级学生订制校服要了解每位新生的上衣和裤子的尺寸;
③要检测一批灯泡的使用寿命;④校正某本书上的印刷错误.
最适合做全面调查的有(??
)
A.?1个???B.?2个????C.?3个???D.?4个
3.为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,随机抽取50名中学生进行该问卷调查,根据调查的结果绘制成如图所示的条形统计图,该调查的方式与图中a的值分别是( )
A.?普查,26??B.?普查,24??C.?抽样调查,26????D.?抽样调查,24
4.下列事件:(1)调查长江现有鱼的数量;(2)调查你班每位同学穿鞋的尺码;(3)了解一批电视机的使用寿命;(4)校正某本书上的印刷错误.最适合做全面调查的是(?????).
A.?(1)(3)B.?(1)(4)
C.?(2)(3)??D.?(2)(4)
5.下列说法中不正确的是( )
A.?要反映我市一周内每天的最低气温的变化情况宜采用折线统计图
B.?打开收音机正在播放TFBOYS的歌曲是必然事件
C.?方差反映了一组数据的稳定程度
D.?为了解一种灯泡的使用寿命.应采用抽样调查的办法
6.下列调查中,调查方式选择合理的是(??
)
A.?了解某河的水质情况,选择抽样调查?
B.?了解某种型号节能灯的使用寿命,选择全面调查
C.?了解一架Y﹣8GX7新型战斗机各零部件的质量,选择抽样调查???
D.?了解一批药品是否合格,选择全面调查
二、填空题
7.扇形统计图是利用圆和________表示________和部分的关系,圆代表的是总体,即100%,扇形代表________。
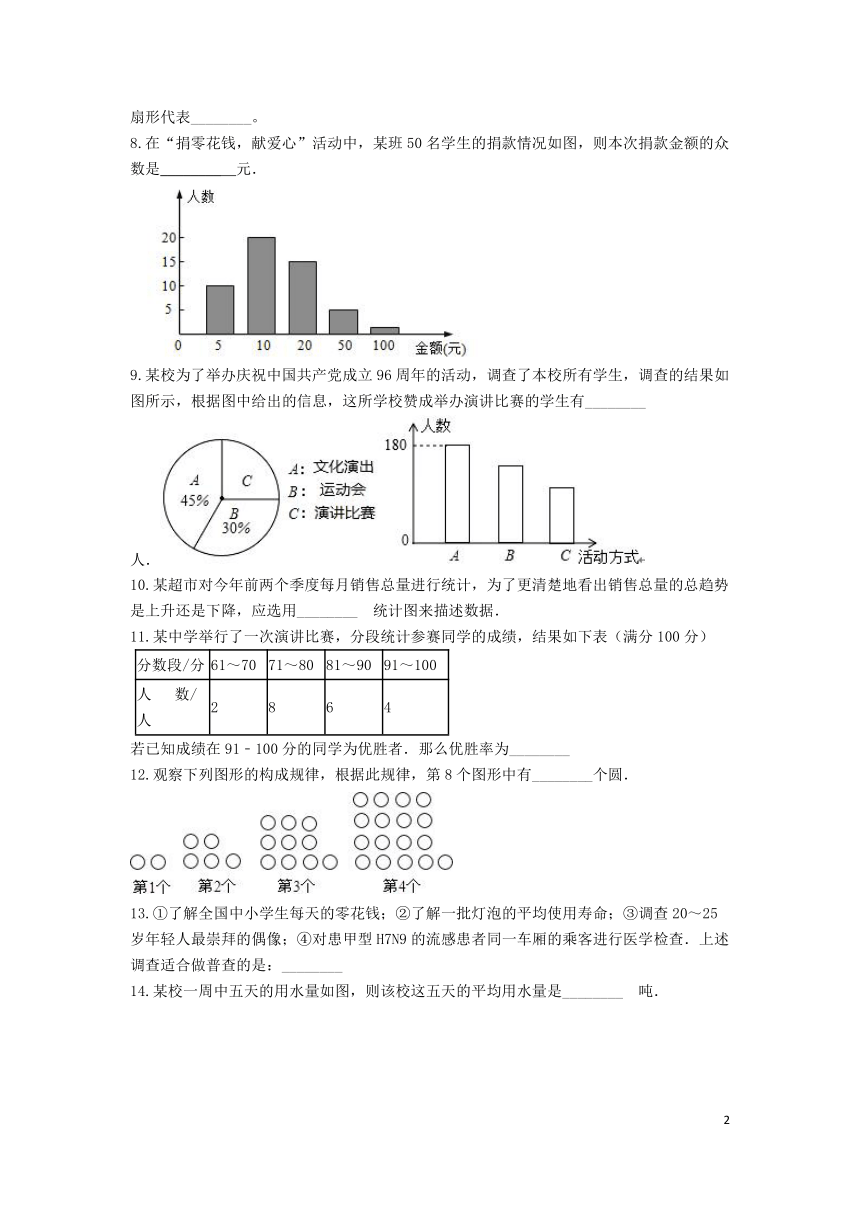
8.在“捐零花钱,献爱心”活动中,某班50名学生的捐款情况如图,则本次捐款金额的众数是________?元.
9.某校为了举办庆祝中国共产党成立96周年的活动,调查了本校所有学生,调查的结果如图所示,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有________人.
10.某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用________?统计图来描述数据.
11.某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(满分100分)
分数段/分
61~70
71~80
81~90
91~100
人?
数/人
2
8
6
4
若已知成绩在91﹣100分的同学为优胜者.那么优胜率为________?
12.观察下列图形的构成规律,根据此规律,第8个图形中有________个圆.
13.①了解全国中小学生每天的零花钱;②了解一批灯泡的平均使用寿命;③调查20~25岁年轻人最崇拜的偶像;④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查.上述调查适合做普查的是:________?
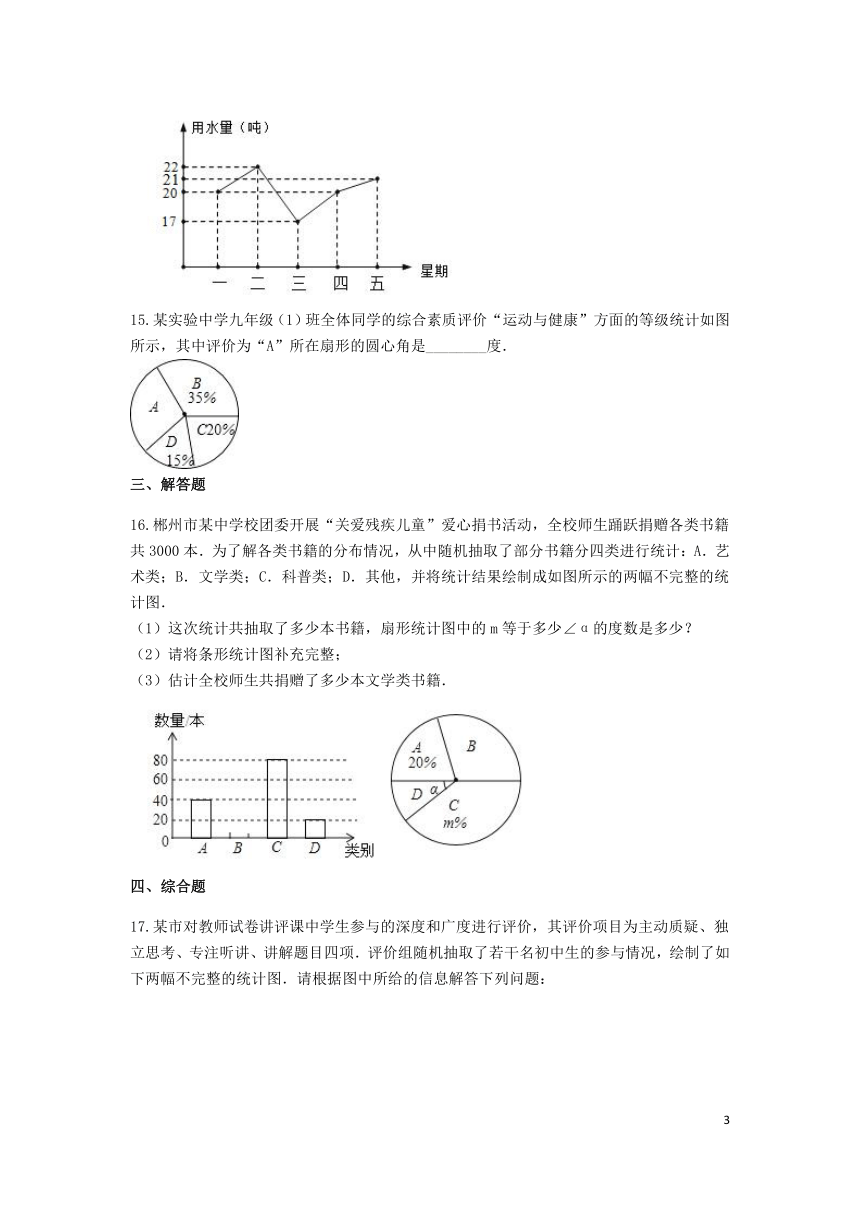
14.某校一周中五天的用水量如图,则该校这五天的平均用水量是________?吨.
15.某实验中学九年级(1)班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,其中评价为“A”所在扇形的圆心角是________度.
三、解答题
16.郴州市某中学校团委开展“关爱残疾儿童”爱心捐书活动,全校师生踊跃捐赠各类书籍共3000本.为了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.
(1)这次统计共抽取了多少本书籍,扇形统计图中的m等于多少∠α的度数是多少?
(2)请将条形统计图补充完整;
(3)估计全校师生共捐赠了多少本文学类书籍.
四、综合题
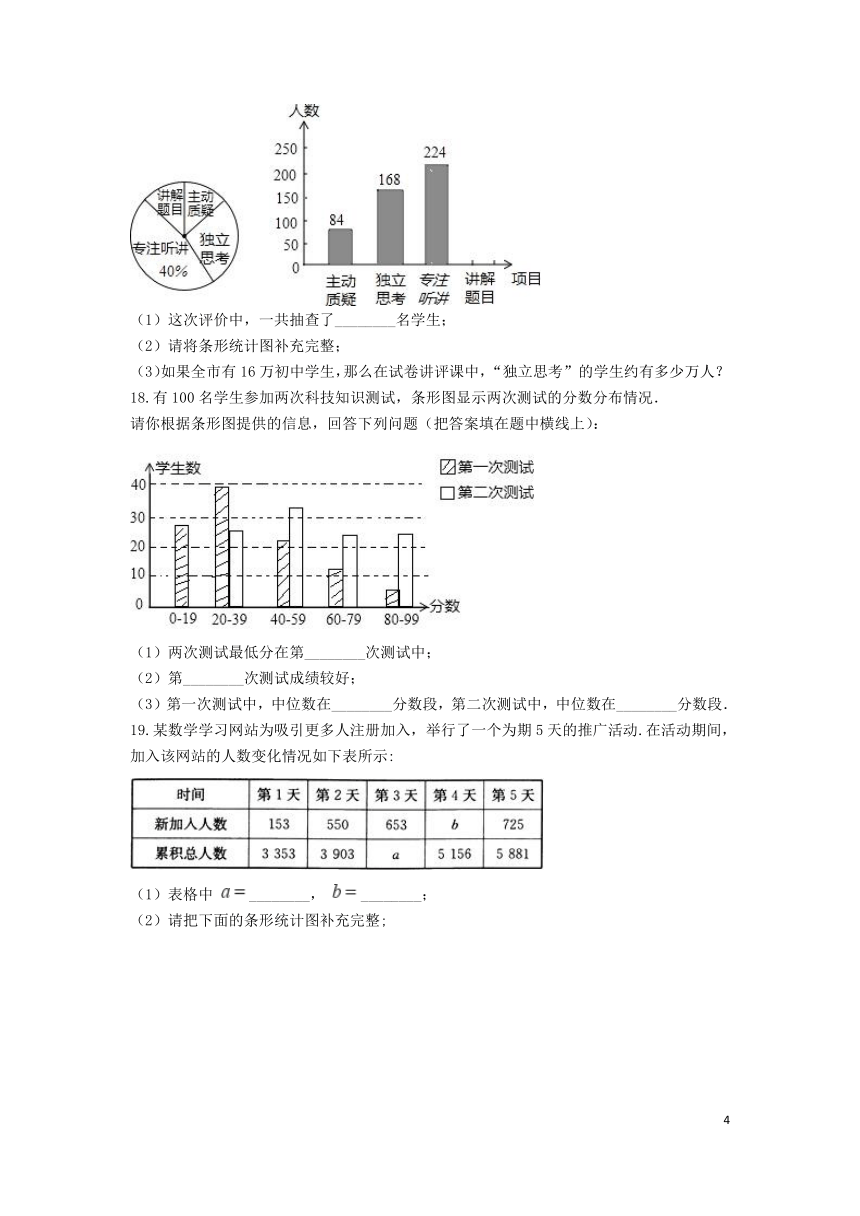
17.某市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中生的参与情况,绘制了如下两幅不完整的统计图.请根据图中所给的信息解答下列问题:
(1)这次评价中,一共抽查了________名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
18.有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上):
(1)两次测试最低分在第________次测试中;
(2)第________次测试成绩较好;
(3)第一次测试中,中位数在________分数段,第二次测试中,中位数在________分数段.
19.某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动.在活动期间,加入该网站的人数变化情况如下表所示:
(1)表格中
________,
________;
(2)请把下面的条形统计图补充完整;
(3)根据以上信息,下列说法正确的是________(只要填写正确说法前的序号).
①在活动之前,该网站已有3
200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2
528人.
20.为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如右表:
体育成绩(分)
人数(人)
百分比(%)
26
8
16
27
a
24
28
15
d
29
b
e
30
c
10
根据上面提供的信息,回答下列问题:
(1)求随机抽取学生的人数;
(2)求统计表中b的值;
(3)已知该校九年级共有500名学生,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.
答案解析部分
一、单选题
1.【答案】A
【考点】全面调查与抽样调查
【解析】【分析】根据适合普查的方式一般有以下几种:①范围较小;②容易掌控;③不具有破坏性;④可操作性较强,进而判断即可。
B、C、均适合抽样调查,因为普查具备破坏性,D、无法进行普查,适合抽样调查,故错误;
A、人数较少,适合采用普查,本选项正确。
【点评】一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查。
2.【答案】B
【考点】全面调查与抽样调查
【解析】【解答】解:①调查长江现有鱼的数量,对象多,捞出每个鱼不易操作,有破坏性,适合做抽样调查;②学校为七年级学生订制校服要了解每位新生的上衣和裤子的尺寸,易操作,必要,适合做全面调查;③要检测一批灯泡的使用寿命,有破坏性,适合做抽样调查;④校正某本书上的印刷错误,非常必要,适合做全面调查,
故答案为:B.
【分析】全面调查适合非常必要或对象个数不多,易操作,抽样调查适合对象多,不易操作或具有破坏性.
3.【答案】D
【考点】全面调查与抽样调查,条形统计图
【解析】【解答】解:调查方式是抽样调查,a=50﹣6﹣10﹣6﹣4=24.
故选D.
【分析】根据抽样调查的定义判断抽查方式,利用总数50减去其它各组的人数即可求得a的值.
4.【答案】D
【考点】全面调查与抽样调查
【解析】【分析】本题需要根据具体情况正确选择普查或抽样调查等方法,调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
【解答】(1)调查长江现有鱼的数量,普查的意义或价值不大,应选择抽样调查;
(2)因为鞋的尺码需使每一个学生都合适才可,故需采用全面调查的方式;
(3)了解一批电视机的使用寿命,调查过程带有破坏性,只能采取抽样调查,而不能将整批电视机全部用于实验;
(4)校正某本书上的印刷错误,是精确度要求高的调查,适于全面调查.
故选D.
5.【答案】B
【考点】扇形统计图
【解析】【解答】解:A、要反映我市一周内每天的最低气温的变化情况宜采用折线统计图,故A正确;
B、打开收音机正在播放TFBOYS的歌曲是随机事件,故B错误;
C、方差反映了一组数据的稳定程度,故C正确;
D、为了解一种灯泡的使用寿命.应采用抽样调查的办法,故D正确;
故选:B.
【分析】根据统计图的特点,可判断A;根据必然事件的定义,可判断B;根据方差的性质,可判断C;根据调查方式,可判断D.
6.【答案】A
【考点】全面调查与抽样调查
【解析】【解答】解:了解妨水河的水质情况,选择抽样调查,A符合题意;
了解每种型号节能灯的使用寿命,选择抽样调查;B不符合题意;
了解一架Y-8GX7新型战斗机各零部件的质量,选择全面调查,C不符合题意;
了解一批药品是否合格,选择抽样调查,D不符合题意.
故答案为:A.
【分析】根据抽样调查一般适合于具有破坏性,危害性,工作量比较大,但数据要求又不需要特点精准的方面的调查;而全面调查适合于数据要求精准,不具有破坏性的调查,根据两种调查适用的范围即可一一判断。
二、填空题
7.【答案】扇形;总量;部分量
【考点】扇形统计图
【解析】【解答】扇形统计图是利用圆和扇形表示总量和部分的关系,圆代表的是总体,即100%,扇形代表部分量.
故答案为:扇形;总量;部分量.
【分析】扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数,通过扇形统计图可以很清楚的表示出各部分数量同总数之间的关系,用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
8.【答案】10
【考点】条形统计图
【解析】【解答】解:根据题意得:捐款5元的10人;捐款10元的20人;捐款20元的15人;捐款50元的5人;捐款100元的1人,
则本次捐款金额的众数是10元,
故答案为:10.
【分析】观察条形统计图,找出捐款数最多的即为众数.
9.【答案】100
【考点】扇形统计图,条形统计图
【解析】【解答】解:由图表可得:总人数为:180÷45%=400(人),故这所学校赞成举办演讲比赛的学生有:400×(1﹣45%﹣30%)=100(人).
故答案为:100
【分析】根据A在两个统计图中的数据先计算总人数,然后根据扇形统计图计算赞成举报演讲比赛的学生的比例,最后乘以400可得对应的人数.
10.【答案】折线
【考点】扇形统计图
【解析】【解答】解:根据题意,得
要求清楚地表示销售总量的总趋势是上升还是下降,结合统计图各自的特点,应选用折线统计图.
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
11.【答案】20%
【考点】统计表
【解析】【解答】解:∵参加这次演讲比赛的同学共有2+8+6+4=20(人),
又∵优胜者有4人,
∴优胜率=4÷20=20%.
故答案为20%.
【分析】先根据表格求出参加演讲比赛的总人数,再用优胜者人数除以总人数即可.
12.【答案】65
【考点】数据分析
【解析】【解答】解:第一个图形有2个圆,即2=12+1;
第二个图形有5个圆,即5=22+1;
第三个图形有10个圆,即10=32+1;
第四个图形有17个圆,即17=42+1;
所以第8个图形有82+1=65个圆.
故答案为:65.
【分析】本题主要考查观察图形的方法可发现规律得出答案.
13.【答案】④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查
【考点】全面调查与抽样调查
【解析】【解答】解:①了解全国中小学生每天的零花钱;②了解一批灯泡的平均使用寿命;③调查20~25岁年轻人最崇拜的偶像;④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查.上述调查适合做普查的是:④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查,
故答案为:④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查.
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
14.【答案】20
【考点】折线统计图
【解析】【解答】解:该校这五天的平均用水量=(20+22+17+20+21)÷5
=100÷5
=20(吨).
故答案为20.
【分析】先从图中得到五天用水量的5个数据,然后根据平均数的概念用这五天的用水量相加的和除以5即可得到平均用水量是多少吨,列式解答即可得到答案.
15.【答案】108
【考点】扇形统计图
【解析】【解答】A所占百分比为:100%-15%-20%-35%=30%
圆心角:
故答案为:108
【分析】注意:扇形图中各部分所占百分比之和等于1
三、解答题
16.【答案】解:(1)40÷20%=200(本),80÷200=40%,×360°=36°,
故答案为:200,40,36°;
(2)B的本数为:200﹣40﹣80﹣20=60(本),
如图所示:
?
(3)3000×=900(本).
答:估计全校师生共捐赠了900本文学类书籍.
【考点】条形统计图,折线统计图
【解析】【分析】(1)用A的本数÷A所占的百分比,即可得到抽取的本数;用C的本数÷总本数,即可求得m;计算出D的百分比乘以360°,即可得到圆心角的度数;
(2)计算出B的本数,即可补全条形统计图;
(3)根据文学类书籍的百分比,即可解答.
四、综合题
17.【答案】(1)560
(2)解:讲解题目的人数=560﹣84﹣168﹣224=84(名),
画条形统计图为:
(3)解:∵16×
=4.8(万),
∴全市在试卷讲评课中,“独立思考”的学生约有4.8万人
【考点】扇形统计图,条形统计图
【解析】【解答】解:(1)抽查的学生总人数=
=560(名);
故答案为560.
【分析】根据抽查的学生总人数=专注听讲的人数除以专注听讲所占的百分比,计算即可。
(2)先算出讲解题目的人数,再补全统计图。
(3)先求出独立思考的学生所占百分比,再用全市初中学生的总人数独立思考的学生所占百分比,计算即可求出结果。
18.【答案】(1)一
(2)二
(3)20﹣39;40﹣59
【考点】条形统计图,数据分析,中位数、众数
【解析】【解答】(1)两次测试最低分在第一次测试中;
(2)第一次测试的低分较多,高分较少,所以第二次的测试成绩较好;
(3)取第50名与51名同学成绩的平均数,所以第一次测试中,中位数落在20﹣39分数段;第二次测试中,中位数落在40﹣59分数段.
【分析】(1)观察统计图易得出答案。
(2)观察统计图可知第一次测试的低分较多,高分较少,第二次测试高分较多,低分少,因此可得出结果。
(3)根据中位数的定义:把数据先按从小到大(或从大到小)的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;即可的出结果。
19.【答案】(1)4556;600
(2)解:如图所示:
(3)①
【考点】统计表,条形统计图
【解析】【解答】解:(1)由题意a=3903+653=4556,b=5156﹣4556=600.
故答案为:4556,600.
(
3
)①正确.3353﹣153=3200.故正确.
②错误.第4天增加的人数600<第3天653,故错误.
③错误.增加的人数=153+550+653+600+725=2681,故错误.
故答案为:①.
【分析】(1)观察表格中的数据通过计算,即可解决问题。
(2)根据第4天的人数600,画出条形图即可。
(3)根据题意逐一判断即可。
20.【答案】(1)50解答:随机抽取学生的人数为8÷16%=50
(2)10解答:∵统计表中a=50×24%=12,c=50×10%=5,
∴统计表中b=50-8-12-15-5=10.
(3)300人解答:∵28分以上(含28分)为优秀,
∴九年级学生体育成绩的优秀率为(15+10+5)÷50=60%,
该校九年级学生体育成绩达到优秀的总人数为500×60%=300人;
【考点】数据分析
【解析】【分析】(1)用第一组的人数除以第一组所占的百分比,求出总人数;(2)先求出a和c的值,再用总人数减去其它各组数的和,求出b的值;(3)先求出体育成绩的优秀率,再乘以九年级学生体育成绩的总人数,求出答案.
1
一、单选题
1.下列调查中,适合采用全面调查(普查)方式的是( )?????
A.?对某班50名同学视力情况的调查?????????????
B.?对元宵节期间市场上汤圆质量情况的调查
C.?对某类烟花爆竹燃放质量情况的调查??????????????????
D.?对重庆嘉陵江水质情况的调查
2.下列事件:①调查长江现有鱼的数量;②学校为七年级学生订制校服要了解每位新生的上衣和裤子的尺寸;
③要检测一批灯泡的使用寿命;④校正某本书上的印刷错误.
最适合做全面调查的有(??
)
A.?1个???B.?2个????C.?3个???D.?4个
3.为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,随机抽取50名中学生进行该问卷调查,根据调查的结果绘制成如图所示的条形统计图,该调查的方式与图中a的值分别是( )
A.?普查,26??B.?普查,24??C.?抽样调查,26????D.?抽样调查,24
4.下列事件:(1)调查长江现有鱼的数量;(2)调查你班每位同学穿鞋的尺码;(3)了解一批电视机的使用寿命;(4)校正某本书上的印刷错误.最适合做全面调查的是(?????).
A.?(1)(3)B.?(1)(4)
C.?(2)(3)??D.?(2)(4)
5.下列说法中不正确的是( )
A.?要反映我市一周内每天的最低气温的变化情况宜采用折线统计图
B.?打开收音机正在播放TFBOYS的歌曲是必然事件
C.?方差反映了一组数据的稳定程度
D.?为了解一种灯泡的使用寿命.应采用抽样调查的办法
6.下列调查中,调查方式选择合理的是(??
)
A.?了解某河的水质情况,选择抽样调查?
B.?了解某种型号节能灯的使用寿命,选择全面调查
C.?了解一架Y﹣8GX7新型战斗机各零部件的质量,选择抽样调查???
D.?了解一批药品是否合格,选择全面调查
二、填空题
7.扇形统计图是利用圆和________表示________和部分的关系,圆代表的是总体,即100%,扇形代表________。
8.在“捐零花钱,献爱心”活动中,某班50名学生的捐款情况如图,则本次捐款金额的众数是________?元.
9.某校为了举办庆祝中国共产党成立96周年的活动,调查了本校所有学生,调查的结果如图所示,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有________人.
10.某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用________?统计图来描述数据.
11.某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(满分100分)
分数段/分
61~70
71~80
81~90
91~100
人?
数/人
2
8
6
4
若已知成绩在91﹣100分的同学为优胜者.那么优胜率为________?
12.观察下列图形的构成规律,根据此规律,第8个图形中有________个圆.
13.①了解全国中小学生每天的零花钱;②了解一批灯泡的平均使用寿命;③调查20~25岁年轻人最崇拜的偶像;④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查.上述调查适合做普查的是:________?
14.某校一周中五天的用水量如图,则该校这五天的平均用水量是________?吨.
15.某实验中学九年级(1)班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,其中评价为“A”所在扇形的圆心角是________度.
三、解答题
16.郴州市某中学校团委开展“关爱残疾儿童”爱心捐书活动,全校师生踊跃捐赠各类书籍共3000本.为了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.
(1)这次统计共抽取了多少本书籍,扇形统计图中的m等于多少∠α的度数是多少?
(2)请将条形统计图补充完整;
(3)估计全校师生共捐赠了多少本文学类书籍.
四、综合题
17.某市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中生的参与情况,绘制了如下两幅不完整的统计图.请根据图中所给的信息解答下列问题:
(1)这次评价中,一共抽查了________名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
18.有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上):
(1)两次测试最低分在第________次测试中;
(2)第________次测试成绩较好;
(3)第一次测试中,中位数在________分数段,第二次测试中,中位数在________分数段.
19.某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动.在活动期间,加入该网站的人数变化情况如下表所示:
(1)表格中
________,
________;
(2)请把下面的条形统计图补充完整;
(3)根据以上信息,下列说法正确的是________(只要填写正确说法前的序号).
①在活动之前,该网站已有3
200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2
528人.
20.为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如右表:
体育成绩(分)
人数(人)
百分比(%)
26
8
16
27
a
24
28
15
d
29
b
e
30
c
10
根据上面提供的信息,回答下列问题:
(1)求随机抽取学生的人数;
(2)求统计表中b的值;
(3)已知该校九年级共有500名学生,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.
答案解析部分
一、单选题
1.【答案】A
【考点】全面调查与抽样调查
【解析】【分析】根据适合普查的方式一般有以下几种:①范围较小;②容易掌控;③不具有破坏性;④可操作性较强,进而判断即可。
B、C、均适合抽样调查,因为普查具备破坏性,D、无法进行普查,适合抽样调查,故错误;
A、人数较少,适合采用普查,本选项正确。
【点评】一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查。
2.【答案】B
【考点】全面调查与抽样调查
【解析】【解答】解:①调查长江现有鱼的数量,对象多,捞出每个鱼不易操作,有破坏性,适合做抽样调查;②学校为七年级学生订制校服要了解每位新生的上衣和裤子的尺寸,易操作,必要,适合做全面调查;③要检测一批灯泡的使用寿命,有破坏性,适合做抽样调查;④校正某本书上的印刷错误,非常必要,适合做全面调查,
故答案为:B.
【分析】全面调查适合非常必要或对象个数不多,易操作,抽样调查适合对象多,不易操作或具有破坏性.
3.【答案】D
【考点】全面调查与抽样调查,条形统计图
【解析】【解答】解:调查方式是抽样调查,a=50﹣6﹣10﹣6﹣4=24.
故选D.
【分析】根据抽样调查的定义判断抽查方式,利用总数50减去其它各组的人数即可求得a的值.
4.【答案】D
【考点】全面调查与抽样调查
【解析】【分析】本题需要根据具体情况正确选择普查或抽样调查等方法,调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
【解答】(1)调查长江现有鱼的数量,普查的意义或价值不大,应选择抽样调查;
(2)因为鞋的尺码需使每一个学生都合适才可,故需采用全面调查的方式;
(3)了解一批电视机的使用寿命,调查过程带有破坏性,只能采取抽样调查,而不能将整批电视机全部用于实验;
(4)校正某本书上的印刷错误,是精确度要求高的调查,适于全面调查.
故选D.
5.【答案】B
【考点】扇形统计图
【解析】【解答】解:A、要反映我市一周内每天的最低气温的变化情况宜采用折线统计图,故A正确;
B、打开收音机正在播放TFBOYS的歌曲是随机事件,故B错误;
C、方差反映了一组数据的稳定程度,故C正确;
D、为了解一种灯泡的使用寿命.应采用抽样调查的办法,故D正确;
故选:B.
【分析】根据统计图的特点,可判断A;根据必然事件的定义,可判断B;根据方差的性质,可判断C;根据调查方式,可判断D.
6.【答案】A
【考点】全面调查与抽样调查
【解析】【解答】解:了解妨水河的水质情况,选择抽样调查,A符合题意;
了解每种型号节能灯的使用寿命,选择抽样调查;B不符合题意;
了解一架Y-8GX7新型战斗机各零部件的质量,选择全面调查,C不符合题意;
了解一批药品是否合格,选择抽样调查,D不符合题意.
故答案为:A.
【分析】根据抽样调查一般适合于具有破坏性,危害性,工作量比较大,但数据要求又不需要特点精准的方面的调查;而全面调查适合于数据要求精准,不具有破坏性的调查,根据两种调查适用的范围即可一一判断。
二、填空题
7.【答案】扇形;总量;部分量
【考点】扇形统计图
【解析】【解答】扇形统计图是利用圆和扇形表示总量和部分的关系,圆代表的是总体,即100%,扇形代表部分量.
故答案为:扇形;总量;部分量.
【分析】扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数,通过扇形统计图可以很清楚的表示出各部分数量同总数之间的关系,用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
8.【答案】10
【考点】条形统计图
【解析】【解答】解:根据题意得:捐款5元的10人;捐款10元的20人;捐款20元的15人;捐款50元的5人;捐款100元的1人,
则本次捐款金额的众数是10元,
故答案为:10.
【分析】观察条形统计图,找出捐款数最多的即为众数.
9.【答案】100
【考点】扇形统计图,条形统计图
【解析】【解答】解:由图表可得:总人数为:180÷45%=400(人),故这所学校赞成举办演讲比赛的学生有:400×(1﹣45%﹣30%)=100(人).
故答案为:100
【分析】根据A在两个统计图中的数据先计算总人数,然后根据扇形统计图计算赞成举报演讲比赛的学生的比例,最后乘以400可得对应的人数.
10.【答案】折线
【考点】扇形统计图
【解析】【解答】解:根据题意,得
要求清楚地表示销售总量的总趋势是上升还是下降,结合统计图各自的特点,应选用折线统计图.
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
11.【答案】20%
【考点】统计表
【解析】【解答】解:∵参加这次演讲比赛的同学共有2+8+6+4=20(人),
又∵优胜者有4人,
∴优胜率=4÷20=20%.
故答案为20%.
【分析】先根据表格求出参加演讲比赛的总人数,再用优胜者人数除以总人数即可.
12.【答案】65
【考点】数据分析
【解析】【解答】解:第一个图形有2个圆,即2=12+1;
第二个图形有5个圆,即5=22+1;
第三个图形有10个圆,即10=32+1;
第四个图形有17个圆,即17=42+1;
所以第8个图形有82+1=65个圆.
故答案为:65.
【分析】本题主要考查观察图形的方法可发现规律得出答案.
13.【答案】④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查
【考点】全面调查与抽样调查
【解析】【解答】解:①了解全国中小学生每天的零花钱;②了解一批灯泡的平均使用寿命;③调查20~25岁年轻人最崇拜的偶像;④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查.上述调查适合做普查的是:④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查,
故答案为:④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查.
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
14.【答案】20
【考点】折线统计图
【解析】【解答】解:该校这五天的平均用水量=(20+22+17+20+21)÷5
=100÷5
=20(吨).
故答案为20.
【分析】先从图中得到五天用水量的5个数据,然后根据平均数的概念用这五天的用水量相加的和除以5即可得到平均用水量是多少吨,列式解答即可得到答案.
15.【答案】108
【考点】扇形统计图
【解析】【解答】A所占百分比为:100%-15%-20%-35%=30%
圆心角:
故答案为:108
【分析】注意:扇形图中各部分所占百分比之和等于1
三、解答题
16.【答案】解:(1)40÷20%=200(本),80÷200=40%,×360°=36°,
故答案为:200,40,36°;
(2)B的本数为:200﹣40﹣80﹣20=60(本),
如图所示:
?
(3)3000×=900(本).
答:估计全校师生共捐赠了900本文学类书籍.
【考点】条形统计图,折线统计图
【解析】【分析】(1)用A的本数÷A所占的百分比,即可得到抽取的本数;用C的本数÷总本数,即可求得m;计算出D的百分比乘以360°,即可得到圆心角的度数;
(2)计算出B的本数,即可补全条形统计图;
(3)根据文学类书籍的百分比,即可解答.
四、综合题
17.【答案】(1)560
(2)解:讲解题目的人数=560﹣84﹣168﹣224=84(名),
画条形统计图为:
(3)解:∵16×
=4.8(万),
∴全市在试卷讲评课中,“独立思考”的学生约有4.8万人
【考点】扇形统计图,条形统计图
【解析】【解答】解:(1)抽查的学生总人数=
=560(名);
故答案为560.
【分析】根据抽查的学生总人数=专注听讲的人数除以专注听讲所占的百分比,计算即可。
(2)先算出讲解题目的人数,再补全统计图。
(3)先求出独立思考的学生所占百分比,再用全市初中学生的总人数独立思考的学生所占百分比,计算即可求出结果。
18.【答案】(1)一
(2)二
(3)20﹣39;40﹣59
【考点】条形统计图,数据分析,中位数、众数
【解析】【解答】(1)两次测试最低分在第一次测试中;
(2)第一次测试的低分较多,高分较少,所以第二次的测试成绩较好;
(3)取第50名与51名同学成绩的平均数,所以第一次测试中,中位数落在20﹣39分数段;第二次测试中,中位数落在40﹣59分数段.
【分析】(1)观察统计图易得出答案。
(2)观察统计图可知第一次测试的低分较多,高分较少,第二次测试高分较多,低分少,因此可得出结果。
(3)根据中位数的定义:把数据先按从小到大(或从大到小)的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;即可的出结果。
19.【答案】(1)4556;600
(2)解:如图所示:
(3)①
【考点】统计表,条形统计图
【解析】【解答】解:(1)由题意a=3903+653=4556,b=5156﹣4556=600.
故答案为:4556,600.
(
3
)①正确.3353﹣153=3200.故正确.
②错误.第4天增加的人数600<第3天653,故错误.
③错误.增加的人数=153+550+653+600+725=2681,故错误.
故答案为:①.
【分析】(1)观察表格中的数据通过计算,即可解决问题。
(2)根据第4天的人数600,画出条形图即可。
(3)根据题意逐一判断即可。
20.【答案】(1)50解答:随机抽取学生的人数为8÷16%=50
(2)10解答:∵统计表中a=50×24%=12,c=50×10%=5,
∴统计表中b=50-8-12-15-5=10.
(3)300人解答:∵28分以上(含28分)为优秀,
∴九年级学生体育成绩的优秀率为(15+10+5)÷50=60%,
该校九年级学生体育成绩达到优秀的总人数为500×60%=300人;
【考点】数据分析
【解析】【分析】(1)用第一组的人数除以第一组所占的百分比,求出总人数;(2)先求出a和c的值,再用总人数减去其它各组数的和,求出b的值;(3)先求出体育成绩的优秀率,再乘以九年级学生体育成绩的总人数,求出答案.
1
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
